منحنيات رائعة وخصائصها. منحنيات مستوية خاصة معادلة دائرية حدودية

إرسال عملك الجيد في قاعدة المعرفة أمر بسيط. استخدم النموذج أدناه

سيكون الطلاب وطلاب الدراسات العليا والعلماء الشباب الذين يستخدمون قاعدة المعرفة في دراساتهم وعملهم ممتنين جدًا لك.

نشر على http://www.allbest.ru/

مؤسسة تعليمية

"دولة بيلاروسيا التربوية

جامعة مكسيم تانك

كلية الفيزياء والرياضيات

قسم الرياضيات وطرق تدريس الرياضيات

دورة العمل على الموضوع

"سيكلويد"

مينسك ، 2016

قوس دائري مشدود البندول

• مقدمة
• 1. الخصائص الأساسية للدوراني
• 2. التعريف الهندسي للحلقة الدائرية
• 3. منطقة قوس الدويري
• 4. طول قوس القوس الحلقي
• 5. حجم الجسم الذي تم الحصول عليه من خلال تدوير قوس دائري
• 6. أفضل بندول
• استنتاج
• فهرس

المقدمة

موضوع عملي بالطبع هو cycloid. هذا المنحنى رائع من نواح كثيرة. إنه أيضًا تتبع نقطة حافة العجلة الدوارة ، وهو أيضًا منحنى التذبذبات لفترة ثابتة ، وهو أيضًا منحنى أسرع هبوط. في الوقت الحاضر ، تُستخدم المنحنيات الحلقية في العديد من الحسابات الفنية ، وتسهل معرفة هذه المنحنيات دراسة أجزاء الماكينة. دون الخوض في التفاصيل ، نذكر أن خصائص المنحنيات الحلقية تُستخدم في بناء ملامح أسنان التروس وفي العديد من القضايا التقنية الأخرى. حتى من وجهة نظر تطبيقية بحتة ، فإن هذه المنحنيات تستحق الاهتمام الأكثر جدية. لذلك ، اعتبرت هذا الموضوع مناسبًا وممتعًا للدراسة.

ما هي المشاكل التي تنشأ في دراسة سيكلويد؟ بادئ ذي بدء ، من الضروري إعطائها تعريفًا هندسيًا بحتًا ، بغض النظر عن الميكانيكا. بعد ذلك ، تحتاج إلى دراسة خصائصه ، والنظر في المماس ، وحساب المساحة التي يحدها قوس الحلقة الدائرية وقاعدتها ، وطول القوس ، وحجم الجسم المتكون من دوران قوس الحلقة الدائرية حول خط التوجيه.

سيأخذ عمل الدورة التدريبية في الاعتبار بالتفصيل الخاصية المتزامنة للدوران الدائري وتطبيقه لإنشاء أفضل بندول. لا يمكن التقليل من أهمية ساعات البندول ، لأنها حتى وقت قريب كانت بمثابة الساعات الأكثر دقة التي ضمنت خدمة الوقت في المراصد الفلكية.

ميزة أخرى للدوران الحلقي ، والتي يجب ملاحظتها ، هي أنه استخدم من قبل العلماء في تطوير تقنيات لدراسة الخطوط المنحنية ، مما أدى إلى اختراع حساب التفاضل والتكامل. في عملي ، أقترح مقارنة حساب طول قوس القوس الحلقي ، ومساحة السطح تحت القوس وأحجام الأجسام المتكونة من دوران القوس الحلقي قبل ظهور حساب التفاضل والتكامل المتكامل ، طويل وليس دائمًا صارم تمامًا ، ويستخدم التكامل.

هدف:دراسة المواد حول موضوع "Cycloid" ؛ دراسة ملامح أفضل البندول. مقارنة دراسة الخطوط المنحنية قبل ظهور حساب التفاضل والتكامل المتكامل وبعده ، وحساب طول قوس القوس الحلقي ، ومساحة السطح تحت القوس وأحجام الأجسام المتكونة من دوران القوس الحلقي.

1. الخصائص الرئيسية للدورة

تحتاج أولاً إلى معرفة نوع المنحنى المسمى بالحلقة الحلقية.

ضع في اعتبارك دائرة نصف قطرها أمتمركزة عند النقطة أ. دع الدائرة المعنية تدور دون الانزلاق على طول محور OX. يسمى المنحنى الموصوف بأي نقطة على الدائرة دائري.

لم يرضي هذا التعريف للدوراني العلماء أبدًا: ففي النهاية ، يعتمد على المفاهيم الميكانيكية - السرعات ، إضافات الحركات ، إلخ. لذلك ، سعت المقاييس الهندسية دائمًا إلى إعطاء الدائرية "تعريفًا هندسيًا بحتًا". ولكن من أجل إعطاء مثل هذا التعريف ، يجب عليك أولاً وقبل كل شيء دراسة الخصائص الأساسية للدوران الدائري ، باستخدام تعريفه الميكانيكي. باختيار أبسط هذه الخصائص وأكثرها تميزًا ، يمكننا استخدامها كأساس لتعريف هندسي.

لنبدأ بدراسة الظل العمودي للخط الدائري. ماذا او ما ظلإلى خط معوج ، يتخيل الجميع بوضوح كافٍ ؛ لذلك لن نقدمه هنا. عادييسمى عمودي على الظل ، ويتم ترميمه عند نقطة الاتصال. على التين. يوضح الشكل 1.1 المماس والطبيعي للمنحنى AB عند نقطته M.

اعتبر دائري (الشكل 1.2). تدور الدائرة في خط مستقيم AB. لنفترض أن نصف القطر العمودي للدائرة ، والذي مر في اللحظة الأولى من أدنى نقطة في الحلقة الدائرية ، تمكن من الالتفاف بزاوية χ وشغل الموضع OM. بعبارة أخرى ، نعتقد أن المقطع M o T جزء من المقطع M o M 1 بحيث تكون الزاوية q من انعطاف كامل. في هذه الحالة ، وصلت النقطة M 0 إلى النقطة M.

النقطة M هي النقطة الدائرية التي تهمنا.

سهم أوهيمثل سرعة مركز الدائرة المتداول. جميع نقاط الدائرة ، بما في ذلك النقطة M ، لها نفس السرعة الأفقية ، ولكن بالإضافة إلى ذلك ، فإن النقطة M تشارك في دوران الدائرة. يتم توجيه السرعة MC ، التي تستقبلها النقطة M على الدائرة أثناء هذا الدوران ، بشكل عرضي السيدة 1 على الدائرة ، أي عمودي على نصف القطر OM.ومنذ ذلك الحين في هذه الحالة ، تكون سرعة MS مساوية من حيث الحجم لسرعة MP (أي السرعة هو).لذلك ، سيكون متوازي الأضلاع للسرعات في حالة حركتنا معينًا (معين من MSKR في الشكل 1.2). قطري MK لهذا المعين سيعطينا فقط مماسًا للدوران الدائري.

كل ما سبق يجعل من الممكن حل مشكلة البناء التالية: بالنظر إلى خط التوجيه AB للدائرة الحلقية ، ونصف القطر r لدائرة التوليد ، والنقطة M التي تنتمي إلى الحلقة الدائرية (الشكل 1.2). مطلوب لبناء ظل من عضو الكنيست إلى دائري.

بوجود نقطة M ، يمكننا بسهولة بناء دائرة توليد ، في موضعها عندما تقع النقطة على الدائرة في M. للقيام بذلك ، نجد المركز أولاً اباستخدام نصف القطر MO= ص (يجب أن تقع النقطة O على خط مستقيم موازٍ لـ AB ، على مسافة r منه). ثم نقوم ببناء قطعة MP ذات طول تعسفي ، موازية لخط التوجيه. بعد ذلك نبني خطا السيدة 1 , عمودي OM. على هذا الخط ، نتخلى عن النقطة مقطعة MC تساوي MP. على MS و MP ، كما هو الحال على الجانبين ، نبني المعين. سيكون قطري هذا المعين المماس للدوران الدائري عند النقطة M.

هذا البناء هندسي بحت ، على الرغم من أننا حصلنا عليه باستخدام مفاهيم الميكانيكا. الآن يمكننا أن نقول وداعًا للميكانيكيين والحصول على المزيد من العواقب بدون مساعدتها. لنبدأ بنظرية بسيطة.

نظرية 1. الزاوية بين مماس إلى دائري (عند نقطة تعسفية)وخط التوجيه يساوي تكملة 90 درجةنصف زاوية دوران نصف قطر الدائرة المولدة.

وبعبارة أخرى ، في الشكل. 1.2

? KLTيساوي أو

سنثبت الآن هذه المساواة. لتقصير الكلام ، سنتفق على تسمية الزاوية φ لدوران نصف قطر الدائرة المولدة بـ "الزاوية الأساسية". هذا يعني أن زاوية MOT في الشكل. 1.2 - الزاوية الرئيسية. سنفترض أن الزاوية الرئيسية حادة. بالنسبة للحالة عندما تقوم الدائرة المتدحرجة بأكثر من ربع دورة كاملة ، سيكون الدليل متشابهًا.

ضع في اعتبارك الزاوية CMP. جانب CM عمودي OM(مماس الدائرة عمودي على نصف القطر). الجانب MP (أفقي) عمودي على من(نحو العمودي). لكن الزاوية MOP ، حسب الحالة ، حادة ، والزاوية CMP منفرجة. هكذا الزوايا منظمة العمل الدوليةو SMRأضف ما يصل إلى 180 درجة (الزوايا ذات الجوانب المتعامدة بشكل متبادل ، أحدهما حاد والآخر منفرج).

إذن ، الزاوية CMP تساوي 180 ° -ts. ولكن ، كما تعلم ، فإن قطري المعين يشطر الزاوية عند الرأس. لذلك يا هوغو

KMR = 90 درجة - ،

Q.E.D.

دعونا الآن نحول انتباهنا إلى الوضع الطبيعي إلى الدويري. دعنا نصور الجانب الأيسر من الشكل. 1.2 أكبر ، ودعنا نرسم قيمة طبيعية أنا (أنا ؟ عضو الكنيست ؛ أرز. 1.3).

من التين. 1.3 يتبع ذلك أن الزاوية EMP تساوي فرق الزوايا KMEو KMR، بمعنى آخر. يساوي 90 درجة - ? KMP.

لكننا أثبتنا للتو أن الزاوية نفسها KMRيساوي 90 درجة -

وهكذا نحصل على:

? RME= 90 درجة -؟ KMR= 90 درجة - (90 درجة -) =

لقد أثبتنا نظرية بسيطة ولكنها مفيدة. دعونا نصيغها:

نظرية 2.الزاوية بين العمودي والدويري (في أي وقت فيه)وخط الدليل يساوي نصف "الزاوية الرئيسية".

دعنا نربط "نقطة (T) الدائرة المولدة الآن بالنقطة M" (النقطة "الحالية" للدائرة الحلقية) بالنقطة "السفلية" (مع نقطة التلامس لدائرة التوليد وخط التوجيه - الشكل 1.3). من الواضح أن Triangle MOT هو متساوي الساقين (OM و منهي أنصاف أقطار الدائرة المولدة). مجموع الزوايا عند قاعدة هذا المثلث يساوي 180 درجة - ش ، وكل زاوية من الزوايا في القاعدة عبارة عن بساط من هذا المجموع. لذا، ? OMT = 90 درجة -.

انتبه إلى الزاوية RMT.إنه يساوي فرق الزاوية HTAو ريال عماني. لقد رأينا ذلك الآن ? OMTيساوي 90 درجة - ؛ أما بالنسبة للزاوية OMP ، فليس من الصعب معرفة ما يساويها. بعد كل شيء ، الزاوية ريال عمانييساوي الزاوية DOM(الزوايا المتقاطعة الداخلية عندما تكون متوازية).

من الواضح أن ? DOM يساوي 90 درجة - ج. وسائل، ؟ OMP = = 90 درجة - ج. وهكذا نحصل على:

RMT = ? HTA - ? ريال عماني \ u003d 90 درجة - - (90 درجة - ج) \ u003d.

اتضح نتيجة رائعة: الزاوية RMTتبين أن تكون مساوية للزاوية PME (بواسطة النظرية 2). لذلك ، سيتم دمج مباشرة ME و MT! أرزنا. 1.3 لم يتم القيام به بشكل صحيح تماما! يتم إعطاء الترتيب الصحيح للخطوط في الشكل. 1.4

دعونا نصيغ النتيجة التي تم الحصول عليها في شكل نظرية 3.

النظرية 3 (الخاصية الرئيسية الأولى للدوران الحلقي).يمر الخط العمودي إلى الدويري عبر النقطة "السفلية" للدائرة المولدة.

هذه النظرية لها نتيجة طبيعية بسيطة. الزاوية بين المماس والعادي ، بحكم التعريف ، هي الزاوية القائمة. هذه هي الزاوية المحددة في محيط الدائرة المولدة. لذلك ، يجب أن يعتمد على قطر الدائرة. لذا، TT 1 - القطر ، و T 1 - النقطة "العلوية" لدائرة التوليد. دعونا نصيغ النتيجة التي تم الحصول عليها.

النتيجة (الخاصية الرئيسية الثانية للالسيكلويد).يمر المماس للدوران عبر النقطة "العلوية" لدائرة التوليد.

لشرح هذه الخاصية ، نحتاج إلى بناء دائري.

يتم تنفيذ بناء السيكلويد بالتسلسل التالي:

1. على خط التوجيه الأفقي ، يتم وضع قطعة AA 12 ، تساوي طول دائرة توليد نصف القطر r ، (2pr) ؛

2. أنشئ دائرة توليد نصف قطرها r ، بحيث يكون خط التوجيه مماسًا لها عند النقطة A ؛

3. الدائرة والقطعة AA 12 مقسمتان إلى عدة أجزاء متساوية ، على سبيل المثال 12 ؛

4. من نقاط القسمة 1 1 ، 2 1 ، ... 12 1 استعادة الخطوط العمودية للتقاطع مع استمرار المحور الأفقي للدائرة عند النقاط 0 1 ، 0 2 ، ... 0 12 ؛

5. من نقاط التقسيم للدائرة 1 ، 2 ، ... 12 ، يتم رسم خطوط أفقية مستقيمة ، والتي تتكون من أقواس دائرة نصف قطرها r ؛

6. النقاط التي تم الحصول عليها A 1 ، A 2 ، ... A 12 تنتمي إلى دائري.

على التين. 1.6 قاعدة الحلقة الدائرية مقسمة إلى 6 أجزاء متساوية ؛

كلما زاد عدد الأقسام ، كلما كان الرسم أكثر دقة. في كل نقطة من الحلقة الدائرية التي أنشأناها ، نرسم ظلًا يربط نقطة المنحنى بالنقطة "العلوية" للدائرة المولدة. في الرسم لدينا سبعة مماسات (اثنان منهم عموديان). الآن رسم دائري يدويًا ، سنحرص على أنه يلامس حقًا كل من هذه الظلال: سيؤدي ذلك إلى زيادة دقة الرسم بشكل كبير. في هذه الحالة ، فإن الحلقة الدائرية نفسها سوف تدور حول كل هذه الظلال).

دعونا ننفذ نفس الشكل. 1.6 المعايير الموجودة في جميع النقاط الموجودة في الحلقة الدائرية. في المجموع ، سيكون هناك خمس قواعد عادية ، دون احتساب الدليل. من الممكن بناء غلاف هذه القواعد يدويًا. إذا أخذنا 12 أو 16 نقطة قسمة بدلاً من ستة ، فسيكون هناك المزيد من القواعد الطبيعية في الرسم ، وسيتم تحديد المغلف بشكل أكثر وضوحًا. يلعب مثل هذا الغلاف لجميع القواعد دورًا مهمًا في دراسة خصائص أي خط منحني. في حالة cycloid ، يتم الكشف عن حقيقة غريبة: مغلف الأعراف من cycloid هو بالضبط نفس دائري ، يتم إزاحته فقط بمقدار 2 أباستمرار راإلى اليمين. هذه الحقيقة هي سمة من سمات الدويري.

2. تعريف هندسي لدورة

نعطي الآن تعريفًا للدوران الدائري كموقع للنقاط دون استخدام الميكانيكا. من الأسهل القيام بذلك. ضع في اعتبارك خطًا تعسفيًا AB(سنعتبر اتجاهه بشكل مشروط أفقيًا) ونقطة عليه م 0 . بعد ذلك ، ضع في اعتبارك جميع الدوائر الممكنة لنصف قطر معين والتي تكون مماسًا لهذا الخط والموجودة على جانب واحد منه. في كل دائرة من هذه النقطة تيلمسها بخط مستقيم ABنضع جانبا (في اتجاه النقطة م 0 ) قوس تم ،يساوي طول المقطع م 0 ت.مركز النقاط م(مأخوذة في جميع الدوائر التي ذكرناها) وستكون دائرية.

دعونا نؤسس خاصية واحدة أكثر أهمية للدوران ونحاول استخدامها كأساس لدراسة هذا المنحنى.

فكر في مثلث MTT 1 (الشكل 2.1) ، يتكون من القطر العمودي لدائرة التوليد ، والظل الدائري والعادي لها.

ركن MT 1 تي، كما هو مرسوم في دائرة ، يساوي نصف الزاوية المركزية بناءً على نفس القوس ، أي يساوي. دعونا ننفق MK || AB و أنا?AB.سيلعب الجزء ME دورًا مهمًا في المستقبل ، لذلك سنعطيه اسمًا وتسمية: سنطلق عليه "ارتفاع" النقطة M للدوران الدائري ونشير إليه بالحرف ح.إذن ارتفاع النقطة م cycloids هي المسافة التي تفصلها عن خط التوجيه.

دعنا ننتبه إلى زاوية KMT. إنها تساوي الزاوية MT 1 تي. من مثلث TMT 1 نحن نحصل:

MT = 2 أالخطيئةومن مثلث TKM:

CT = MT الخطيئة.

بمقارنة هذه النتائج مع ملاحظة أن CT = h ، نحصل أخيرًا على:

ح = 2 أالخطيئة 2.

عبرنا عن ارتفاع النقطة M بدلالة الزاوية بين المماس عند النقطة M والعمودي (ما زلنا نعتبر أن اتجاه الخط المستقيم AB هو الأفقي). الآن دعونا نعبر عن جيب هذه الزاوية من حيث "الارتفاع". من الواضح أننا نحصل على:

حيث من خلال كيتم الإشارة إلى ثابت القيمة للدوران الدائري المعطى . نذكر النتيجة التي تم الحصول عليها في النظرية.

نظرية 4.يتناسب جيب الزاوية بين المماس للدوران عند النقطة M والعمودي مع الجذر التربيعي "لارتفاع" النقطة M.

من الواضح أن أي سيكلويد يمتلك هذه الخاصية. السؤال الذي يطرح نفسه: إلى أي مدى تميز هذه الخاصية بالضبط الدائرة الحلقية: هل سيكون أي منحنى يمتلك هذه الخاصية بالضرورة دائريًا؟ يمكن إثبات أن هذا سيكون هو الحال ، - أن النظرية (العكسية) التالية صحيحة أيضًا:

نظرية 5.بالنظر إلى الخط AB والنقطة M ، فإن المنحنى الوحيد الذي يفي بشروط النظرية 4 ويمر عبر النقطة M هو دائري.

علاوة على ذلك ، فإن نصف قطر الدائرة المولدة لهذا السيكلويد مرتبط بالمعامل كوالتي ورد ذكرها في نظرية 4 بالعلاقة التالية:.

يجدر أيضًا الانتباه إلى منحنى رائع آخر يسمى رفيق الدويري.

النظر في سيكلويد (الشكل 2.2). من نقطته M ، نخفض القطر العمودي لدائرة التوليد. دعنا نحصل على النقطة P. لنقم بهذا البناء لجميع نقاط الحلقة الدائرية بدون استثناء.

ثم ستصف النقطة P بعض المنحنى. يسمى هذا المنحنى رفيق الدويري.

ضع في اعتبارك دائريًا ، ونقطة M عليه والنقطة المقابلة P على القمر الصناعي (الشكل 2.3). سيتم الإشارة إلى مركز الدائرة المولدة بالحرف س. ثم سيكون لدينا:

QP=QMكوس؟ MQP = أكوس (180 0-طن) = - أ cosц = - أالخطيئة (90 0 تس) = أالخطيئة (ج -90 0).

دعونا نرسم موضع مراكز الدائرة المولدة (الخط المستقيم XX 1 ). من النقطة م 0 تأجيل ABالقطعة المستقيمة م 0 ك، مساو. دعونا ننفق كنتاكي ? XX 1 . سيتم الإشارة إلى نقطة تقاطع هذه الخطوط بالحرف ا. القطعة المستقيمة م 0 صعلى خط التوجيه المستقيم من طرف السيكلويد إلى نقطة التلامس مع الدائرة المولدة يساوي أج ، حيث ج هي الزاوية الرئيسية MQص, معبرا عنها بالتقدير الدائري. القطعة المستقيمة اوكعلى المحور الأفقي XX 1 يساوي م 0 ص - م 0 ك=أ(ج -) ، والمقطع QPيساوي أخطيئة؟ PMQ ، أي يساوي جيب الزاوية (ج -) مضروبًا في نصف القطر أ.

إذن من هذه النقطة اأفقيًا ، يتم رسم الأجزاء المتساوية في الطول لأقواس الدائرة ، وعلى طول الخطوط الرأسية لجيوب الزوايا المقابلة لهذه الأقواس. هذا هو بناء الجيب العادي المعروف لنا.

وسائل، رفيق الدويري يسمى الجيب.

لن نتعمق في دراسة خصائص هذا المنحنى الرائع حقًا ، بل سنلاحظ فقط كحقيقة المنطقة التي يحدها رفيق قوس من الدويري وقاعدته تساوي ضعف مساحة دائرة التوليد.

3. مربع قوس الدورة

أول ذكر لحساب المنطقة المحصورة بين قوس الحلقة الدائرية وقاعدتها موجود في أعمال Viviani و Torricelli. في الوقت نفسه ، استخدموا تقنية خاصة ، والتي كانت تسمى "طريقة غير قابلة للتجزئة". تتكون هذه الطريقة من حقيقة أن الشكل المنحني ينقسم إلى شرائح رفيعة بشكل لا نهائي ، ومن السهل نسبيًا العثور على المنطقة ، ثم يتم إضافة هذه المناطق. أدت هذه التقنية إلى ظهور حساب التفاضل والتكامل بعد نصف قرن.

خذ بعين الاعتبار شكلًا يحده قوس دائري وجيب جيبي. في الشكل 3.1 ، هذا الشكل ، المكون من بتلتين ، محاط بدائرة بخط سميك. دعونا نحسب مساحتها.

بادئ ذي بدء ، لنقم ببناء صورة معكوسة للبتلة اليمنى للشكل بالنسبة إلى الخط المستقيم الموجه AB (هذا الانعكاس يرد في الشكل 4.1 بخط متقطع). دعونا بعد ذلك نحرك هذا المنحنى المتقطع لأعلى إلى اليسار ونطبقه على البتلة اليسرى بحيث تتطابق أقواس أشباه الجيوب الموجودة في محيط كل بتلة. نحصل على شكل محدب ، مظلل في الشكل 3.1 ويظهر بشكل منفصل في الشكل. 3.2 هذا الرقم يسمى شخصية روبرفال. دعونا نحدد أهم خصائص هذا الشكل.

1. الشكل المحدب M 0 RLM مساوٍ في الحجم لشكل البتلة الموضح بالخط السميك في الشكل 3.1. يمكن ملاحظة ذلك من حقيقة أنه "مكون" من نفس البتلات.

2. أي وتر أفقي لشكل محدب يساوي ضعف وتر البتلة على نفس المسافة من AB. في الواقع ، فإن الحبلين CE و PH (الشكل 3.1) للبتلة اليمنى ، على مسافة متساوية من الدائرة المولدة ، بعيدان بشكل متساوٍ عن المركز. لذلك CT \ u003d CE \ u003d PH \ u003d P 1 H 1 \ u003d TL.

يعطي هذا نتيجة مهمة: الوتر MR لشكل محدب (الشكل 3.2) يساوي وتر الدائرة المولدة SK ، الواقعة على نفس المسافة من خط التوجيه.

دعونا نفكر الآن في الشكل المحدب لروبرتال والدائرة المماس لنفس الخطين AB و A 1 B 1 ، وربط نقاط تقاطعهم مع الدائرة ومع محيط الشكل المحدب على التوالي بواسطة مقاطع الخط المستقيم ، مثل هو مبين في الشكل. المضلعات المنقوشة التي تم الحصول عليها بهذه الطريقة (HLMNPQRSTK و H 1 L 1 M 1 N 1 P 1 Q 1 R 1 S 1 T 1 K 1) سوف تسمى المضلعات "المقابلة" على سلسلة من شبه المنحرف (والمثلثات). مناطق شبه المنحرف "المقابلة" في الدائرة وفي شكل روبرفيل ، على سبيل المثال ، NPRS و N 1 P 1 R 1 S 1 ، متساوية ، لأن هذه شبه المنحرفات ، على التوالي ، لها نفس القواعد السفلية ، القواعد العلوية (المقابلة الحبال) والارتفاعات. على التين. 3.2 يتم تغطية شبه المنحرف المتكافئة الحجم المتساوية بنفس الفقس.

سنزيد الآن عدد الخطوط المستقيمة "المتوسطة" الموازية لـ AB إلى أجل غير مسمى ، بحيث تميل المسافة بين أي زوج متجاور إلى الصفر. ثم في الدائرة نحصل على سلسلة من المضلعات المنقوشة ، يزداد عدد أضلاعها إلى ما لا نهاية ، ويميل كل جانب إلى الصفر. نعلم أن المساحات S n لهذه المضلعات محدودة بمساحة الدائرة:

ليم س ن= ص أ 2 .

كيف سيتصرف تسلسل المضلعات المنقوشة في شكل محدب روبرفال في هذه الحالة؟ ميدان؟ n سوف تميل المضلعات المنقوشة المتتالية إلى المساحة؟ شخصيات روبرفال. من المعروف أنه إذا احتفظ متغيرين بقيم متساوية مقابل جميع تغييراتهما ويميل أحدهما إلى حد معين ، فإن الآخر يميل إلى نفس الحد. لكن كل مضلع مدرج في شكل روبرفال يساوي في الحجم المضلع المقابل المدرج في الدائرة. لذلك نستنتج أن حدود مساحات المضلعات المدرجة في شكل روبرفال تساوي حدود مساحات المضلعات المقابلة المدرجة في دائرة ؛ مما يعني أن مساحة الشكل المحدب روبرفال تساوي مساحة الدائرة المولدة:

من هذا نحصل على نتيجة فورية: مساحة الشكل ثنائي البتلة تساوي مساحة الدائرة المولدة.

لنلقِ نظرة الآن على الشكل 3.1. مساحة الشكل AOTPBKA ، كما رأينا ، تساوي ضعف مساحة دائرة التوليد. لقد حددنا للتو مساحة الشكل ثنائي البتلة: إنها تساوي مساحة الدائرة المولدة. بالتالي، المساحة التي يحدها قوس الدائرة الحلقية وقاعدتها تساوي ثلاثة أضعاف مساحة الدائرة المولدة.

لنجد الآن المساحة المحصورة بين قوس الدائرية وقاعدتها باستخدام الهندسة التفاضلية.

أين ر? .

لنجد المشتق

4. طول قوس الدائرة

تم حساب طول القوس للدوران لأول مرة من قبل المهندس المعماري وعالم الرياضيات الإنجليزي رين في عام 1658. انطلق رين من الاعتبارات الميكانيكية التي تذكرنا بالعمل المبكر لتوريشيلي وروبرتفال. اعتبر دوران الدائرة المتدحرجة بزاوية صغيرة جدًا بالقرب من النقطة "السفلية" للدائرة المولدة. من أجل إعطاء اعتبارات Wren الموحية قوة إثباتية ، يجب على المرء أن يأخذ في الاعتبار عددًا من النظريات المساعدة ، وبالتالي سيتعين على المرء أن ينفق الكثير من العمل.

من الأنسب استخدام مسار أطول ولكن ألطف. للقيام بذلك ، تحتاج إلى التفكير في منحنى خاص لكل منحنى مسطح - اكتساحه.

اعتبر قوسًا محدبًا AB لخط منحني (الشكل 4.1). دعونا نتخيل أن خيطًا مرنًا غير مرن له نفس طول القوس AB نفسه متصل بالقوس AB عند النقطة A ، وهذا الخيط "ملفوف" على المنحنى ويلتصق به بإحكام ، بحيث تتوافق نهايته مع النقطة B سنقوم "بفتح" - تصويب الخيط ، وإبقائه مشدودًا ، بحيث يتم دائمًا توجيه الجزء الحر من خيط CM بشكل عرضي إلى القوس AB. في ظل هذه الظروف ، ستصف نهاية الخيط بعض المنحنى. يسمى هذا المنحنى بالمسح ، أو باللاتينية ، مطويالمنحنى الأصلي.

إذا لم يكن قوس المنحنى محدبًا في كل مكان في اتجاه واحد ، إذا كان مثل المنحنى AB في الشكل. 4.2 لها نقطة C يمر عندها ظل المنحنى من جانب إلى آخر (تسمى هذه النقطة نقطة الانعطاف) ، ثم في هذه الحالة يمكننا أيضًا التحدث عن تطور المنحنى ، لكن المنطق سيكون له لتكون أكثر تعقيدًا بعض الشيء.

تخيل أن الخيط ثابت فقط عند نقطة الانعطاف C (الشكل 4.2). سيصف الخيط ، المتعرج من القوس BC ، منحنى BMP - مسح.

تخيل الآن خيطًا ملفوفًا حول القوس AC للمنحنى الأصلي ، لكن هذا الخيط ممدود بالفعل: عند النقطة C ، يتم إرفاق قطعة من الخيط CP به. من خلال لف خيط ACP ممدود بمنحنى SA ، نحصل على قوس RNA الذي ، مع قوس BMP ، يشكل منحنى واحد مستمر - مستمر ، ولكن ليس سلسًا في كل مكان: نقطة الانحراف C للمنحنى الأصلي سوف تتوافق مع الطرف (نقطة العودة) لمنحنى VMRNA: سيكون منحنى VMRNA انحرافًا (اكتساحًا) لمنحنى ICA.

ساعدتنا هذه الأمثلة على التعود على المفاهيم الجديدة للتطور والتطور. الآن دعونا ندرس كشف المنحنيات الحلقية.

بدراسة هذا المنحنى أو ذاك ، قمنا غالبًا ببناء منحنى مساعد - "رفيق" لهذا المنحنى. لذلك ، نحن نتكلف الجيوب الأنفية - رفيق سيكلويد. الآن ، بدءًا من الحلقي المعطى ، نقوم ببناء دائري مساعد مرتبط به ارتباطًا وثيقًا. اتضح أن الدراسة المشتركة لمثل هذا الزوج من cycloids أسهل في بعض النواحي من دراسة حلقة واحدة. سوف نسمي مثل هذا الدويري المساعد دويريًا مصاحبًا.

النظر في نصف قوس من AMB دائرية (الشكل 4.3). يجب ألا نشعر بالحرج من أن هذا الدوامة يقع بطريقة غير عادية ("رأساً على عقب"). لنرسم 4 خطوط موازية لخط التوجيه AK على مسافات أ, 2أ, 3أو 4 أ. دعونا نبني دائرة توليد في الموضع المقابل للنقطة M (في الشكل 4.3 ، يشار إلى مركز هذه الدائرة بالحرف O). سيتم الإشارة إلى زاوية دوران MON بواسطة c. ثم المقطع AN سيكون مساويًا لـ bc (يتم التعبير عن الزاوية u بالتقدير الدائري).

نواصل قطر HT لدائرة التوليد بعد النقطة T حتى يتقاطع (عند النقطة E) مع الخط المستقيم PP. على TE كقطر ، نقوم ببناء دائرة (مع مركز O 1). دعونا نبني ظلًا عند النقطة M إلى الدائرة الدائرية AMB. للقيام بذلك ، يجب أن تكون النقطة M ، كما نعلم ، متصلة بالنقطة T. نواصل المماس MT بعد النقطة T إلى التقاطع مع الدائرة المساعدة ، وسنسمي نقطة التقاطع M 1. هذه هي النقطة M 1 التي نريد الآن التعامل معها.

أشرنا إلى الزاوية MON بـ c. لذلك ، فإن الزاوية MTH ستكون مساوية (الزاوية المحيطية بناءً على نفس القوس). من الواضح أن المثلث TO 1 M 1 متساوي الساقين. لذلك ، ليس فقط الزاوية O 1 TM 1 ، ولكن أيضًا الزاوية TM 1 O 1 ستكون متساوية. وبالتالي ، فإن حصة الزاوية TO 1 M 1 في المثلث TO 1 M 1 تظل بالضبط p - q راديان (تذكر أن الزاوية 180؟ تساوي p راديان). نلاحظ أيضًا أن الجزء NK يساوي بوضوح b (p - c).

فكر الآن في دائرة مركزها O 2 ، كما هو موضح في الشكل 4.3 بخط متقطع. من الرسم يتضح نوع الدائرة. إذا قمت بتدحرجه دون الانزلاق على طول الخط المستقيم CB ، فإن نقطته B ستصف الحلقة الدائرية BB. عندما تدور الدائرة المتقطعة خلال الزاوية p - c ، سيصل المركز O 2 إلى النقطة O 1 ، وسيأخذ نصف القطر O 2 B الموضع O 1 M 1. وهكذا ، فإن النقطة M 1 التي أنشأناها هي نقطة من دائري BB.

يعين البناء الموصوف لكل نقطة M من الدائرة الحلقية AMB نقطة M 1 من الحلقة الدائرية VM 1 B. في الشكل. 4.4 تظهر هذه المراسلات بشكل أكثر وضوحًا. يُطلق على الدويري الذي تم الحصول عليه بهذه الطريقة الاسم الدائري المصاحب. على التين. 4.3 و 4.4 ، فإن cycloids التي تصورها خطوط متقطعة جريئة مصاحبة فيما يتعلق بالسيكلويد الموصوفة بخطوط صلبة جريئة.

من التين. 4.3 يمكن ملاحظة أن الخط MM 1 هو الخط الطبيعي عند النقطة M 1 إلى الدائرة الحلقية المصاحبة. في الواقع ، يمر هذا الخط عبر النقطة M 1 من الدائرة الحلقية ومن خلال النقطة T من التماس بين دائرة التوليد وخط التوجيه (النقطة "الأدنى" من الدائرة المولدة ، كما اعتدنا أن نقول ؛ الآن تحولت إلى كن "الأعلى" ، لأن الرسم مستدير). لكن هذا الخط نفسه ، من خلال البناء ، مماس لـ "قاعدة" AMB الدائرية. وبالتالي ، فإن الدويري الأصلي يلامس كل طبيعي من الدويري المصاحب. إنه مغلف الأعراف من cycloid المصاحبة ، أي تطورها. وتبين أن الدائرية "المصاحبة" هي مجرد جزء لا يتجزأ من الحلقة الحلقية الأصلية!

من خلال العمل على هذا البناء المرهق ، ولكنه بسيط في الأساس ، أثبتنا نظرية رائعة اكتشفها العالم الهولندي Huygens. ها هي النظرية: تطور cycloid هو بالضبط نفس دائري ، يتم إزاحته فقط.

بعد أن شيدنا تطورًا ليس لقوس واحد ، ولكن إلى الدائرة الحلقية بأكملها (والتي ، بالطبع ، لا يمكن القيام بها إلا عقليًا) ، ثم تطورًا لهذا التطور ، وما إلى ذلك ، نحصل على الشكل. 4.5 تشبه البلاط.

دعونا ننتبه إلى حقيقة أنه عند إثبات نظرية Huygens ، لم نستخدم تقديرات متناهية الصغر أو غير قابلة للتجزئة أو تقريبية. لم نستخدم حتى الميكانيكا ، على الرغم من أننا استخدمنا أحيانًا تعبيرات مستعارة من الميكانيكا. هذا الدليل بالكامل من روح المنطق الذي استخدمه علماء القرن السابع عشر عندما أرادوا إثبات النتائج التي تم الحصول عليها بدقة بمساعدة مختلف الاعتبارات الإيحائية.

نتيجة طبيعية مهمة تتبع مباشرة من نظرية Huygens. ضع في اعتبارك المقطع AB في الشكل. 4.4 من الواضح أن طول هذا الجزء يساوي 4 أ. تخيل الآن أن خيطًا ملفوفًا على قوس دائري AMB ، مثبتًا عند النقطة A ومجهزًا بقلم رصاص عند النقطة B. إذا قمنا "بلف" الخيط ، فإن القلم سوف يتحرك على طول تطور دائري AMB ، أي على طول الحلقة الدائرية BM 1 ب. من الواضح أن طول الخيط ، الذي يساوي طول نصف قوس الحلقة الدائرية ، سيكون مساويًا للمقطع AB ، أي ، كما رأينا ، 4 أ. لذلك ، فإن الطول L للقوس الدائري للحلقة الدائرية سيكون مساويًا لـ 8 أ، والصيغة L = 8 أيمكن اعتباره الآن مثبتًا بشكل كافٍ.

نحسب طول القوس باستخدام الهندسة التفاضلية. سيكون الحل الذي تم الحصول عليه بهذه الطريقة أقصر وأسهل بكثير:

أين ر?

ص(ر) =

=

| ص(ر) |=== 2sin

5. حجم الجسم الذي تم الحصول عليه عن طريق تدوير قوس السيكلويد

دعونا نجد حجم الجسم الناتج عن دوران القوس الحلقي حول قاعدته. وجده روبرفال عن طريق كسر الجسم الناتج على شكل بيضة (الشكل 5.1) إلى طبقات رقيقة للغاية ، ونقش الأسطوانات في هذه الطبقات وإضافة أحجامها. الدليل طويل ومضجر وغير صارم تمامًا. لذلك ، لحسابها ، ننتقل إلى رياضيات أعلى. دعونا نضع المعادلة الحلقية حدوديًا.

في حساب التفاضل والتكامل ، عند دراسة المجلدات ، يستخدم الملاحظة التالية:

إذا تم إعطاء المنحنى الذي يحيط شبه المنحني المنحني بواسطة المعادلات البارامترية وكانت الوظائف في هذه المعادلات تفي بشروط النظرية الخاصة بتغيير المتغير في تكامل معين ، فإن حجم جسم دوران شبه المنحرف حول محور الثور سوف تحسب بالصيغة:

لنستخدم هذه الصيغة لإيجاد الحجم الذي نحتاجه.

بنفس الطريقة نحسب سطح هذا الجسم.

L = ((x، y): x = a (t - sin t)، y = a (1 - cost)، 0؟ t؟ 2р)

في حساب التفاضل والتكامل ، توجد الصيغة التالية لإيجاد مساحة سطح جسم ثورة حول المحور x لمنحنى محدد على قطعة بارامترية (t 0؟ t؟ t 1):

بتطبيق هذه الصيغة على معادلة السيكلويد الخاصة بنا ، نحصل على:

ضع في اعتبارك أيضًا سطحًا آخر ناتجًا عن دوران القوس الدائري. للقيام بذلك ، سنقوم ببناء انعكاس مرآة للقوس الدائري بالنسبة لقاعدته ، وسنقوم بتدوير الشكل البيضاوي الذي شكله الحلقة الدائرية وانعكاسه حول محور KT (الشكل 5.2)

أولاً ، لنجد حجم الجسم المتكون من دوران القوس الحلقي حول محور KT. سيحسب حجمه بالصيغة (*):

وهكذا ، حسبنا حجم نصف جسم اللفت. ثم سيكون الحجم الإجمالي

لإيجاد مساحة سطح هذا الجسم الثوري باستخدام التكامل ، من الضروري أيضًا تقسيمه إلى نصفين أفقيًا والنظر في الجزء العلوي منه.

إذن مساحة سطح الجسم الناتج هي

6. أفضل بندولوم

اكتشف جاليليو ، وهو يشاهد الثريا المتأرجحة في المعبد ، أن زمن التأرجح الكامل للثريا ، أي الوقت الذي سيعود بعده إلى موضعه الأصلي (ما يسمى ب فترة التذبذب) ، كان هو نفسه لكل من المساحات الكبيرة والصغيرة. قادت هذه الملاحظة جاليليو إلى الاعتقاد بأن الجسم المتأرجح (بندول) يمكن استخدامه للتحكم في تشغيل الساعة.

فشل جاليليو نفسه في صنع ساعة ذات بندول ، وسرعان ما أصبح واضحًا أن ملاحظاته كانت غير دقيقة. أظهرت الملاحظات الأكثر دقة أن فترة تذبذب البندول هي أكبر ، كلما كان التأرجح أكبر ؛ ولكن بسبب الاحتكاك الحتمي للمحور ومقاومة الهواء ، فإن تأرجح البندول العادي يتناقص باستمرار ، مما يعني أن فترة التذبذب ستنخفض أيضًا. ساعة ذات بندول عادي - تسمى بخلاف ذلك البندول الدائري(لأن كل نقطة منه تصف قوسًا لدائرة) لا يمكن أن تسير بشكل صحيح.

اكتشف Huygens كيفية صنع بندول دائري بحيث يكون له تأرجح مستمر. لكنه حل أيضًا مشكلة أخرى مثيرة للاهتمام - أجاب على السؤال حول أي منحنى يجب أن تتحرك النقطة بحيث لا تعتمد فترة اهتزازاتها على السعة. لقد توصل إلى تصميم يحرك مركز ثقل البندول على طول هذا المنحنى.

لنبدأ بجهاز يضمن الحركة الصحيحة لساعة ذات بندول دائري. هيأ لكن(الشكل 6.1) يقودها سلسلة ذات وزن فيفي نهايةالمطاف. يتم تثبيت ترس على محور هذه العجلة ، متصل بها بإحكام. هذا الترس يقود عقارب الساعة ، وبالتالي من الضروري أن تكون العجلة لكن تحركت بالتساوي.

لكن الوزن في، مثل أي جسم ، سيتحرك تحت تأثير الجاذبية بشكل متسارع ، مما يضفي دورانًا متسارعًا على العجلة لكن. يجب أن يقضي البندول على الصعوبة مم.

مِرسَاة منالكذب في طائرة العجلة لكن، متصلة بإحكام بالبندول مم ، مم البندول نفسهيقع خلف مستوى الرسم وبالتالي يتم رسمه بخط منقط. مرساة مجهزة بأسنان حو إلى.

في اللحظة الموضحة في الشكل. 6.1 عجلة لكنممسوك بالشق الأيسر حالمراسي من.عندما يتأرجح البندول إلى اليسار ، يكون الشق حستحرر المرساة ترس العجلة الذي تم التقاطه ، وستدور العجلة ، ولكن فقط بواسطة الزاحف ، لأن الترس إلىسوف تسقط المراسي في الفجوة بين أسنان العجلة وتؤخرها. عندما يتأرجح البندول إلى اليمين مرة أخرى ، فإن الشق الموجود على هذا الجانب سيتم تثبيته بواسطة المرساة. لذلك ، مع كل تأرجح كامل للبندول (ذهابًا وإيابًا) ، ستدير العجلة سنًا واحدًا بالضبط ، أي لجزء معين من الدائرة. ستكون حركة العجلة موحدة بشكل صارم. أسنان المرساة ، كما يتضح من الشكل. يتم قطع 6.1 بشكل غير مباشر ، بحيث يجب أن تنزلق سن العجلة ، التي تم تثبيتها للخلف بواسطة المرساة وتحريرها مرة أخرى ، على السطح المائل لأسنان المحرك. نتيجة لذلك ، ستعطي المرساة للبندول دفعة صغيرة. ستعوض هذه الدفعات الإيقاعية عن فقدان الطاقة الذي ينفقه البندول في التغلب على الاحتكاك ومقاومة الهواء. لذلك ، لن ينقص تأرجح البندول. وبالتالي ، فإن الوزن ينقل الطاقة إلى كل من عجلات الساعة والبندول نفسه ، بينما ينظم البندول مسار الساعة.

ماذا لو توقفت الساعة؟ ليس من الصعب استخدامها: يكفي رفع الوزن وتأرجح البندول. ولكن في الوقت نفسه ، قد يتحول التأرجح إلى أن يكون مختلفًا ، وستذهب الساعة بشكل متساوٍ ، ولكن بشكل غير صحيح (ستمضي قدمًا أو تبدأ في التأخر). ابتكر Huygens جهازًا يتيح لك ضبط مسار الساعة بسهولة. لكن Huygens ، كعالم حقيقي ، كان مهتمًا بالسؤال: ما الذي يجب أن يكون بندولًا "مثاليًا" ، بندول لا يعتمد وقت تأرجحه على حجم التأرجح؟ دعونا نفكر بالتفصيل في كيفية حل Huygens لهذه المشكلة.

كلمة "tautochrone" تعني "الزي". هذه هي الطريقة التي أطلق عليها Huygens اسم المنحنى الذي بدأ في البحث عنه ، أي مثل هذا المنحنى الذي يجب أن يتحرك على طوله مركز ثقل البندول بحيث لا تعتمد فترة تأرجحه على حجم التأرجح. توج البحث بالنجاح: تبين أن الزمن الدقيق الغامض كان دائريًا تمت دراسته قريبًا. في القيام بذلك ، أظهر Huygens ذكاء استثنائي. يكفي أن نقول إن عقيدة التطورات قد تم إنشاؤها في عملية حل هذه المشكلة بدقة.

مسبب Huygens على النحو التالي. تخيل أخدودًا على شكل دائري ، كما هو موضح في الشكل. 6.2

تتدحرج كرة ثقيلة على طول هذا الأخدود م. سننظر في الحالة المثالية - حالة عدم وجود مقاومة للاحتكاك والهواء.

قم بالإشارة إلى نقاط الانعطاف للدوراني بواسطة م 0 و م? 0 , ونصف قطر دائرة التوليد من خلال أ. ارسم دائرة نصف قطرها أمماس للدائرة الحلقية عند الرأس (تتمركز الدائرة ا) وإنشاء دائرة في الموضع المقابل للنقطة مسيكلويدس (معطى بالخط المتقطع). لنفترض أننا وضعنا الكرة عند النقطة م 1 أخدود واتركها تذهب دون دفع. تحت تأثير الجاذبية ، سوف يتدحرج. دعونا ندرس حركته.

ماذا ستكون سرعة الكرة عندما تصل إلى النقطة مسيكلويدس؟ من السهل حسابها. تنازليا من النقطة م 1 نقطة م، سوف تستهلك الكرة بعض الطاقة الكامنة. فقدان الطاقة هذا يساوي ناتج وزن الكرة ملغ(م -- وزن الكرة ، ز- تسارع الجاذبية) إلى "فقدان الارتفاع" ، أي على الفرق في ارتفاع الكرة في المواقف م 1 و معلاوة على ذلك ، يتم قياس الارتفاعات من مستوى معين ، على سبيل المثال ، من مستوى الأرض. مهما كان المستوى الذي تحسبه الارتفاعات ، فإن اختلافها في حالتنا سيكون مساويًا للمقطع NM. لذا ، فإن فقدان الطاقة الكامن للكرة سيكون مساويًا لـ ملغ· جلالة الملك.

ولكن بموجب قانون الحفاظ على الطاقة ، فإن الطاقة الكامنة المفقودة للكرة ستتحول إلى الطاقة الحركية لحركتها ، والتي ، كما تعلمون ، تساوي ، إذا أشرنا إلى السرعة غير المعروفة للكرة من خلال. معادلة هذه الطاقة الحركية بالطاقة الكامنة المفقودة ، نحصل على المعادلة

التي نجد منها على الفور قيمة السرعة المطلوبة

من السهل أيضًا تحديد اتجاه هذه السرعة. سيتم توجيهه مماسًا إلى دائري ، أي على طول الوتر ML(الشكل 6.2) ، أين إل- النقطة "الأدنى" في الدائرة المولدة.

لن نهتم بالسرعة نفسها بقدر اهتمامنا بإسقاطها العمودي ، أي "سرعة نزول الكرة" ، معدل تغير ارتفاعها. من السهل حساب هذا الإسقاط العمودي: فهو يساوي ، أين الزاوية بين الوتر MLوعمودي. وتر فيدائرة مع المركز ا، من الواضح أنها متساوية ومتوازنة مع الوتر ML، وبالتالي الزاوية LMPيساوي الزاوية قطة، وهو مذكور في الشكل. 6.2 لذا:

سنقارن الحركة غير المستوية على طول دائري بالحركة المنتظمة على طول الدائرة. تحقيقا لهذه الغاية ، نقوم ببناء دائرة مساعدة على النحو التالي: من خلال الرأس لكنيتم رسم دائري عمودي ميلادي(قطر الدائرة مع المركز ا) ، ومن خلال نقطة البداية M 1 لحركة الكرة ، يتم رسم موازٍ M 1 B إلى قاعدتها. دع نقطة تقاطع هذه المتوازيات والعمودية يتم الإشارة إليها بالحرف في. الدائرة مبنية عليها AB، كما هو الحال في القطر ، وستكون الدائرة المساعدة المطلوبة. ليس من الواضح بعد كيف هو بالضبط أفضل من الدوائر الأخرى.

لنبدأ بحقيقة أننا سنربط المكون الرأسي لسرعة الكرة بعناصر الدائرة المساعدة. نملك:

لان NM = VC.من مثلث فعلنحن نحصل:

ولكن ال = 2 أكوس , وبالتالي

نعوض بقيمة جيب التمام التي تم إيجادها في التعبير عن السيدمميزة بعلامة النجمة (*). نحن نحصل:

الجذر الأخير يساوي متوسط ​​التناسب بين الأجزاء VCو AK، بمعنى آخر. بين أجزاء الوتر ABمثلث ABC، حيث يتم تقسيم الأخير إلى الارتفاع SC. لكن هذا التناسب المتوسط ​​، وفقًا للنظرية المعروفة بشأن الخطوط المتناسبة في مثلث قائم الزاوية ، يساوي تمامًا الارتفاع SC:

VK · AK = SK 2 .

لذلك ، بالنسبة للمكون الرأسي السيدسرعة الكرة على طول الدائرة الحلقية نحصل عليها أخيرًا:

MP =· كانساس.

كميات أ و ز أعطيت لنا من البداية وليست مرتبطة بنقطة مولا مع موقعها الأولي م 1 . وهكذا ، يتحدد الوتر تمامًا حركة الكرة على طول الدويري كانساسالدائرة المساعدة ، أي موضع نقطة النهاية منفي هذه الدائرة.

ضع في اعتبارك الحركة المنتظمة للنقطة منعلى طول دائرة مساعدة ذات سرعة زاوية تساوي راديان في الثانية ، أي درجة في الثانية. في هذه الحالة ، سرعة النقطة منعلى طول الدائرة سيكون مساويًا لمنتج نصف قطر الدائرة والسرعة الزاوية ، معبراً عنها بالراديان (في الثانية) ، أي مساوي ل

ما مدى سرعة النقطة التي تنخفض؟ من, ما مدى سرعة تغير المسافة بينه وبين الخط المستقيم؟ م 0 م؟ 0 مع حركة موحدة للنقطة منحول المحيط؟ هذا سهل الحساب.

سرعة يتم توجيه حركة نقطة الدائرة بشكل عرضي إلى الدائرة ، أي عمودي على نصف القطر. إسقاطها على العمودي يساوي السرعة نفسها مضروبة في جيب تمام الزاوية الشكل 6.3. لكن من الواضح أن الزاوية تساوي الزاوية المسؤولية الاجتماعية للشركات 1: يتم الحصول على كليهما بطرح الزاوية ا 1 ممن الزاوية اليمنى. جيب تمام الزاوية المسؤولية الاجتماعية للشركات 1 يساوي . للإسقاط العمودي لسرعة الحركة المنتظمة في دائرة نجد:

يتم الحصول على نتيجة ملحوظة: عندما تتحرك نقطة بشكل موحد على طول دائرة ، فإن إسقاطها على الخط الرأسي يتحرك تمامًا بنفس الطريقة التي يتحرك بها الإسقاط على عمودي الكرة التي تتدحرج على طول دائري. إن إسقاط كلتا السرعتين في أي لحظة من الزمن متساويان. ولكن يتبع من هذا أن نقطة الدائرة من في في لكنوالكرة على دائري من م 1 في لكنسيأتي في نفس الوقت. من السهل تحديد هذا الوقت. لقد قلنا بالفعل أن نقطة على الدائرة المساعدة تجعل الراديان ثانية ، بمعنى آخر ، ستدور راديانًا واحدًا في ثوانٍ ، والراديان في. نحتاج إلى نفس الوقت بالضبط لكي تتدحرج الكرة أسفل الحلقة الدائرية من النقطة م 1 نقطة لكن. سوف يستغرقه نفس الوقت للارتقاء من خلال القصور الذاتي إلى النقطة م؟ 1 ، ونفس الشيء - للنزول مرة أخرى ، ونفس الشيء - للارتفاع والعودة إلى موضع البداية (إلى النقطة مواحد). هذا يعني أن وقت التذبذب الكامل للكرة (فترة التذبذب) سيكون مساويًا لـ:

هذه صيغة رائعة جدا. نرى أن فترة حركة الكرة على طول الأخدود الدائري يتم تحديدها تمامًا من خلال أبعاد الأخدود (نصف قطر الدائرة المولدة للحلقة الدائرية) وتسارع الجاذبية. موقف النقطة م 1 على الحلقة الدائرية ، المسافة من الخط المستقيم م 0 م؟ 0 لا يهم. من أي نقطة تبدأ فيها الكرة في الحركة الدائرية ، ستكون فترة اهتزازها هي نفسها.

فكر Huygens في كيفية استخدام خاصية توتر الزمن للدوران الحلقي لبناء بندول "مثالي". كيف تجعل كرة البندول تتحرك بشكل متزامن دون اللجوء إلى الأخاديد والأجهزة المماثلة مع الكثير من الاحتكاك؟ بالتفكير في هذا ، توصل Huygens إلى مفاهيم التطور وغير المطلق.

دعونا نصنع قالبًا يتكون من نصفين متطابقين من القوس الدائري لهما نتوء مشترك ا(الشكل 6.4). نشير إلى نصف قطر الدائرة المولدة ، كما هو الحال دائمًا ، بواسطة أ. سنقوي القالب عموديًا وعند أعتابته ااربط خيطًا بطول يساوي 4 أ-- بمعنى آخر. ضعف قطر الدائرة المولدة للدوران الدائري. خيط نهاية مجاني تيأعطها كرة ثقيلة.

ستصف الكرة أثناء حركتها فتح الدويري ASOEV، لأن الخيط سوف يلتف حول القالب. لكن كشف الدويري هو بالضبط نفس الدائرية. لذا فإن المنحنى VMTRA، التي تتحرك الكرة على طولها ، سيكون دائريًا ناتجًا عن دائرة نصف قطرها أ.

إذا وضعنا الكرة في نقطة اعتباطية مواتركها لنفسها ، ستبدأ في التذبذب ، ولن تعتمد فترة هذه التذبذبات على اختيار النقطة م. حتى إذا انخفض تأرجح التذبذبات تحت تأثير الاحتكاك ومقاومة الهواء ، فإن وقت تذبذب البندول يظل دون تغيير. حقا هذا البندول سيكون متوترا الزمن!

دعونا الآن نفكر في التذبذبات الصغيرة للبندول على طول القوس ABسيكلويدس (الشكل 6.5). إذا كانت هذه التذبذبات صغيرة جدًا ، فلن يتم الشعور بتأثير قالب الدليل عمليًا وسيتحرك البندول تقريبًا مثل بندول عادي بطول ل=4أ, علقت عند نقطة ا. طريق ABالبندول الدائري لا يختلف عمليا عن المسار مطول البندول الدائري 4 أ. وهذا يعني أن فترة التذبذبات الصغيرة لنواس دائري عادي بطول ل=4أ لن تختلف عمليا عن فترة البندول الدائري. الدخول في الصيغة

الذي التقينا به أعلاه ، بدلاً من أيساوي ذلك ، نحصل على التعبير عن فترة التذبذبات الصغيرة للبندول الدائري من حيث طوله:

استنتاج

في عملية إكمال عملي في الدورة التدريبية ، قمت بدراسة المواد المتعلقة بموضوع الحلقة الدائرية ، ودرست ميزات أفضل بندول ، مقارنة بالدراسة الأنيقة إلى حد ما ، ولكنها ليست بسيطة جدًا للدوران الدائري قبل ظهور حساب التفاضل والتكامل المتكامل ، مع أبسطها والأكثر دراية ، درس في الهندسة التفاضلية والتحليل الرياضي ؛ مرة أخرى مقتنعًا بضرورة دراسة هذه التخصصات. كما اتضح ، فإن cycloid له تطبيق عملي ضخم ليس فقط في الرياضيات ، ولكن أيضًا في الحسابات التكنولوجية ، في الفيزياء.

تبين أن العمل على دراسة هذا الموضوع مثير وممتع للغاية.

فهرس

1. بيرمان ج. سيكلويد. - م ، 2007. - 113 ثانية.

2. Savelov A.A. منحنيات مسطحة. - م ، 1960. - 293 ص.

3. Fikhtengolts G.M. أساسيات التحليل الرياضي. -M. ، 2005 ، الإصدار 2. -464 ص.

استضافت على Allbest.ru

...

وثائق مماثلة

تاريخ موجز لدراسة الدوي. التعريف الهندسي وخصائص وميزات بناء السيكلويد. المعادلة الدائرية البارامترية والمعادلة في الإحداثيات الديكارتية. مهام لإيجاد أجزاء من دائري الشكل والأشكال المكونة من سيكلويد.

ورقة المصطلح ، تمت إضافة 01/16/2011


لحظات ومراكز كتلة المنحنيات المستوية. نظرية جولدن. مساحة السطح التي تكونت نتيجة دوران قوس منحنى مستوٍ حول محور يقع في مستوى القوس ولا يتقاطع معه تساوي حاصل ضرب طول القوس وطول الدائرة.

محاضرة تمت الإضافة 09/04/2003


تعريف لا يتجزأ محدد ، خصائصه. طول قوس المنحنى. منطقة شبه منحرف منحني الأضلاع. مساحة سطح الدوران. مناطق الأشكال المقيدة برسوم بيانية للوظائف مقيدة بخطوط معطاة بالمعادلات. حساب حجوم الجثث.

العمل الرقابي ، تمت إضافة 02/10/2017


التكامل المحدد هو وظيفة مضافة رتيبة تم ضبطها على مجموعة من الأزواج ومكوناتها وخصائصها. حساب تكامل محدد ؛ صيغة نيوتن ليبنيز. التطبيقات الهندسية: المساحة ، طول القوس ، حجم جسم الثورة.

العرض التقديمي ، تمت الإضافة في 05/30/2013


إيجاد مساحة شكل محدد برسوم بيانية دالة باستخدام تكامل مزدوج. الحصول بالتناوب على حجم الجسم حول محور OX للشكل ، مقيد بالخطوط المحددة. حدود التكامل في التكامل المزدوج على منطقة محددة بخطوط.

الاختبار ، تمت إضافة 2014/03/28


خطوط ملحوظة من الترتيب الثالث: القائمة الديكارتية ، ديوكليس 'cissoid ، strofrid ، Agnesi verzier. سطور الرتب الرابعة والعالية وبعض الخطوط المتعالية: حلزونية أرخميدس ، منحنى أقصر نزول. منطقة المنطقة التي يحدها lemniscate.

ورقة مصطلح ، تمت إضافتها في 08/07/2015


مفهوم التكامل المحدد ، حساب المساحة ، حجم الجسم وطول القوس ، العزم الثابت ومركز ثقل المنحنى. حساب المنطقة في حالة المنطقة المستطيلة المنحنية. تطبيق التكاملات المنحنية والسطحية والثلاثية.

ورقة مصطلح ، تمت الإضافة بتاريخ 19/05/2011


مشتق تكامل محدد فيما يتعلق بحد أعلى متغير. حساب التكامل المحدد كحد للمبلغ المتكامل بواسطة صيغة نيوتن-لايبنيز ، وتغيير المتغير والتكامل حسب الأجزاء. طول القوس في الإحداثيات القطبية.

العمل الرقابي ، تمت إضافة 08/22/2009


تاريخ حساب التفاضل والتكامل. تطبيقات محددة لا يتجزأ لحل بعض مشاكل الميكانيكا والفيزياء. لحظات ومراكز كتلة منحنيات الطائرة ، نظرية جولدن. المعادلات التفاضلية. أمثلة على حل المشكلات في MatLab.

الملخص ، تمت الإضافة 09/07/2009


تكامل منحني الخطي من النوع الأول والثاني. مساحة المنطقة التي يحدها منحنى مغلق. حجم الجسم الناتج عن دوران منحنى مغلق. مركز الكتلة ولحظات القصور الذاتي للمنحنى. المجال المغناطيسي حول الموصل الحامل الحالي. جوهر قانون فاراداي.

تذكر-تلك-oran-same-layer-mass-co-ka-ta-fo-you - light-from-ra-zha-te-سواء ، المرفقة-la-u-schi-e-sya بإبر الحياكة- لو-سي-بيد-لا-جو-كو-لو-سا؟ At-cre-pim ka-ta-fot إلى sa-mo-mu rim-du ko-le-sa واتبع tra-ek-to-ri-she. وفقًا لمنحنيات lu-chen-nye ، فهي مرتبطة بعائلة cyclo-id.

في الوقت نفسه ، يُطلق على Ko-le-so اسم zy-va-et-sya حول من داخل دائرة (أو دائرة ستو) cyclo-lo-and-dy.

لكن هيا ، دعنا نعود إلى قرننا ونعيد تصميمه على تقنية أكثر حداثة. في الطريق ، وداعا ، سقط كا مو شيك ، علق شخص ما في برو تك تو ري كو لي سا. Pro-ver-now-shis بضع لفات مع co-le-som ، حيث-yes-le-tit ka-men ، متى تغش من pro-tek-to-ra؟ ضد الحق في حركة mo-the-cycle-la أو على اليمين؟

في واقع الأمر ، فإن الحركة الحرة للجسم na-chi-na-et-sya وفقًا لـ ka-sa-tel-noy إلى تلك tra-ek-that-rii ، والتي وفقًا لذلك تحرك السرب. Ka-sa-tel-naya إلى cyclo-lo-and-de دائمًا على اليمين-le-on-right-le-tion للحركة ويمر عبر النقطة العليا ku pro-from-in-dia-Circle-no -sti. في الاتجاه الصحيح ، حركة نفس Le-tit و ka-mu-shek لدينا.

هل تتذكر كيف ركبت في البرك في طفولتك على دراجة هوائية بدون جناح خلفي؟ Mok-para-lo-ka على ظهرك -ta-ta.

القرن السابع عشر هو قرن سيكلو ودي. لقد درس أفضل العلماء خصائصه المذهلة.

نوع من tra-ek-to-riya يجلب الجسم ، يتحرك تحت تأثير قوة الجاذبية ، من نقطة إلى أخرى لفترة قصيرة من عنق الشاي؟ ستكون هذه واحدة من المهام الأولى لذلك na-at-ki ، جنة شخص ما هذه الساعة لا يجلس على اسم رقم va-ri-a-tsi-on-noe.

يمكن أن تكون Mi-ni-mi-zi-ro-vat (أو mak-si-mi-zi-ro-vat) أشياء مختلفة - طول الطريق والسرعة والوقت. في za-da-che حول bra-hi-hundred-chrone mi-ni-mi-zi-ru-et-x name-but time -call-em: اليونانية βράχιστος - الأصغر ، χρόνος - الوقت).

أول ما يتبادر إلى الذهن هو tra-ek-to-riya. تعال ، دعنا نلقي نظرة أيضًا على re-re-ver-well-thuyu cyclo-lo-and-du بنقطة return-vra-ta في الجزء العلوي من الفحص المحدد. واتباع Ga-li-leo Ga-li-le-em ، - أربعة فيرت-تين-كو دائرة-لا-ستي ، ربط-نيا-يو-ششي على-شي النقاط.

لسبب ما ، اعتبر Ga-li-leo Ga-li-ley ras-smat-ri-val four-vert-tin-ku الدوائر واعتبر أن هذا كان الأفضل بمعنى le time-me-no tra-ek-that -riya النسب-كا؟ لقد قام بإدخال lo-ma-nye فيه وأشار إلى أنه مع زيادة عدد الروابط ، سينخفض ​​الوقت. من هنا ، نعم ، ذهب Ga-li-lei بشكل طبيعي إلى الدائرة ، لكنه توصل إلى نتيجة خاطئة مفادها أن هذا tra-something -ria هو الأفضل بين كل ما هو ممكن. كما يمكننا أن نرى ، فإن أفضل ما في الأمر هو la-et-sya cyclo-lo-and-yes.

من خلال نقطتين معينتين ، من الممكن تمرير دورة lo-and-du واحدة بشرط وجود toch-ka vra-ta tsik-lo-and-dy في أعلى نقطة. ونعم ، عندما تأتي دورة lo-and-de-ho-dit-sya تحت-no-mother-sya لتمرير النقطة الثانية ، فستظل تنحدر Cree -howl nai-sko-rei-she-go !

آخر واحد إلى بيوتاي سي فايا لـ دا تشا ، مرتبط بـ cyclo-lo-and-doy ، هو for-da-cha حول ta-at-that-chron. ترجمت ταύτίς من اليونانية ، وتعني "نفس" ، ، كما نعلم بالفعل - "الوقت".

دعونا نصنع ثلاثة جبال واحد على واحد مع pro-fi-lem في شكل cyclo-lo-and-dy ، بحيث تكون نهايات الجبال هي owl-pa-da-li و ras-po-la-ga -lis في الجزء العلوي من دورة lo-and-dy. دعونا نضع ثلاثة bo-ba على مختلف you-so-you و Let's-dim from-mash-ku. حقيقة Udi-vi-tel-ney-shiy - الجميع سينزلون رجلًا واحدًا الآن لكن!

في الشتاء ، يمكنك بناء جبل من الجليد في الفناء والتحقق من هذا العقار مباشرة.

For-da-cha حول ta-at-that-chrono-st-it in na-ho-de-nii مثل هذا العواء الملتوي الذي ، na-chi-naya من any-bo-go-initial- ولكن بنفس الطريقة ، فإن وقت النزول إلى نقطة معينة سيكون هو نفسه.

Hri-sti-en Guy-gens do-ka-zal ، أن الـ ta-at-that-chron-noy الوحيد هو la-et-sya cyclo-lo-and-yes.

Ko-nech-but، Guy-gen-sa ليس منحدرا في منطقة إن-تي-ري-سو-فال على طول الجبال الجليدية. في ذلك الوقت ، لم يكن لدى العلماء مثل هذا النمو في عدم وجود أم من أجل الحب للفن. من أجل-نعم-تشي ، درس بعض الجاودار ، وكان-هو-دي-لي من الحياة ومن أجل البوم من أولئك-لا-كي في ذلك الوقت-لي-لا. في القرن السابع عشر ، كان co-ver-sha-yut-sya بالفعل خططًا بحرية بعيدة. Shi-ro-tu mo-rya-ki هل يمكنك تحديد-de-lyat بالفعل إلى مائة دقيقة ولكن دقيقة ولكن ، ولكن مفاجأة- vi-tel- لكنك لا تعرف كيف تحدد - دي ليات مع كل شيء. وواحدة من ما قبل-la-gav-shih-s-so-bos من-me-re-niya shi-ro-you كانت os-no-van على na-li-chii دقيقة كرونو-لا-خندق.

الأول ، الذي كان من أجل دو صغير دي لات ما-يات-لا-لا-لا يعرف ، شخص ما سيكون دقيقًا ، كان Ga-li-leo Ga-li-ley. ومع ذلك ، في تلك اللحظة التي كان فيها na-chi-na-et them re-a-li-zo-vy-vat ، كان قد تقدم في السن بالفعل ، وكان أعمى ، وفي العام المتبقي ليس لدى العالم الوقت الكافي لعمل مشاهدة في حياته. ومع ذلك ، فقد كان هذا الابن جيدًا ، ومع ذلك ، فإن هذا الطفل المضاء بالعسل و na-chi-na-et for-no-mother-sya ma-yat-no-one ، نفس الموت pe-red و عدم وجود وقت لإعادة ضريبة القيمة المضافة لأننا جلسنا. كانت العلامة التالية على السرب هي Christi-sti-an Guy-gens.

لاحظ أن ري-ري-أو-كو-لي-با-نيا عادة-غو ما-يات-ني-كا ، راس-سمات-ري-فاف-شي-غو-سيا جا-لي- لي-إم ، من أجل- ويجلس من البداية ولكن من نفس الشيء ، أي من am-pli-tu-dy. يجب أن يكون التفكير في الكيفية عبارة عن مسار لحركة الحمل ، بحيث لا يكون وقت الكيفية عليه - كما هو - من am-pli-tu -دي ، أعاد شا-إت فور-دا-تشو حول تا-أت-ذا-كرون. ولكن كيف يمكن تحريك الحمل على طول دورة lo-and-de؟ Pe-re-vo-dya theo-re-ti-che-research-before-va-tion in the العملي-تي-تشي-الطائرة ، الرجل-جين دي-لا-وآخرون "الخدين" ، على شخص الجاودار نا ma-you-va-et-sya ve-roar-ka ma-yat-no-ka ، وأعدِ عددًا قليلاً من مهام ma-te-ma-ti-che. إنه يفعل-كا-زي-فا-إت أن "الخدين" يجب أن يكون لهما ملف تعريف نفس الدورة - لو - ودي - بنفس الطريقة التي استخدمتها إيفو-لو-ذاك-لو-أند-دي ياف-لا- et-sya cycle-lo-and-yes مع نفس pa-ra-met-ra-mi.

بالإضافة إلى ذلك ، فإن بناء ما قبل أنثى جاي جين سوم من سيكلو-لو-أند-بعيد-نو-جو ما-يات-نو-كا يطرح في-لا-إت من خلال حساب طول دورة لو و دى. إذا كان هناك كو لا نقطة زرقاء ، فإن الطول مقابل بعض السرب يساوي أربعة-يريم را-دي-يو-سام حول-من-في-دي- sche-go ، mak- si-mal-ولكن من-clo-thread ثم نهايتها ستكون عند نقطة re-re-se-che-niya "الخدود" و cyclo-lo-and-dy-tra- ek-to-rii ، أي في الجزء العلوي من cyclo-lo-and-dy- “cheek-ki”. بما أن هذا هو في لو في على طول ar-ki cyclo-and-dy ، فإن الطول الكامل يساوي ثمانية ra-di-u-sam المؤيدة للداخل-العم- ث.

صنع Christ-sti-an Guy-gens ما-يات-نيك دوريًا وبعيدًا ، وساعات معه مؤيدة لهو دي ما إذا كانت بي تا نيا في البحر بو-تي-شي- stvi-yah ، لكن لم يأت. ومع ذلك ، تمامًا مثل الساعات مع ma-yat-no-one المعتاد لهذه الأغراض.

من ماذا ، واحد لواحد ، لا يزال su-sche-stu-yut cha-so-me-ha-bottom-نحن مع المعتاد لكن الوريد ny ma-yat-no-one؟ إذا نظرت إليها ، فمع الصغيرة من-كلو-لا-نو-ياه ، مثل ريد-نو-جو ما-يات-نو-كا ، "الخدين" سيكلو-لو- أند-بعيد-لكن-غو- yat-no-ka تقريبًا لا يوجد تأثير eye-zy-va-yut. بالمقابل ، فإن الحركة على طول cyclic-lo-and-de وحول المحيط مع صغير من-clo-no-no-yah تكاد تكون owl-pa- yes-yut.

5. المعادلة البارامترية للدوريات والمعادلة في الإحداثيات الديكارتية

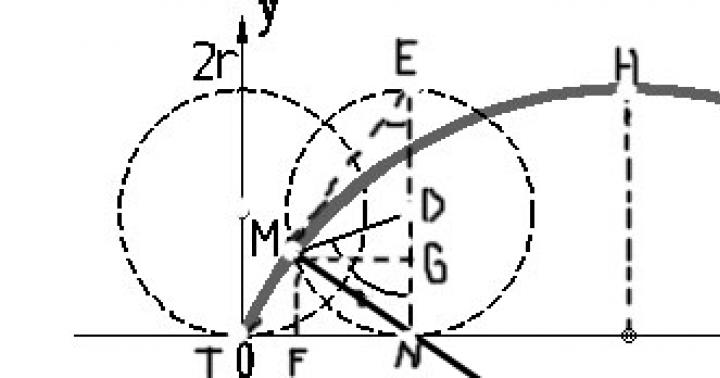
افترض أن لدينا دائرى شكلته دائرة نصف قطرها أ تتمركز عند النقطة أ.

إذا اخترنا كمعامل يحدد موضع النقطة ، فإن الزاوية t = ∟NDM التي تمكن نصف القطر من الدوران ، والتي كان لها وضع رأسي AO في بداية التدحرج ، ثم إحداثيات x و y للنقطة سيتم التعبير عن M على النحو التالي:

x \ u003d OF \ u003d ON - NF \ u003d NM - MG \ u003d at-a sin t ،

y = FM = NG = ND - GD = a - a cos t

لذلك فإن المعادلات البارامترية للدوراني لها الشكل:

عند تغيير t من -∞ إلى + ، تحصل على منحنى يتكون من مجموعة لا حصر لها من هذه الفروع ، والتي تظهر في هذا الشكل.

أيضًا ، بالإضافة إلى المعادلة البارامترية للدوران الدائري ، هناك أيضًا معادلته في الإحداثيات الديكارتية:

حيث r هو نصف قطر الدائرة المكونة للحلقة الدائرية.

6. مشاكل لإيجاد أجزاء من دائري الشكل والأشكال المكونة من سيكلويد

رقم المهمة 1. أوجد مساحة الشكل الذي يحده قوس واحد من دائري والذي تُعطى معادلته بشكل حدودي

والمحور أوه.

المحلول. لحل هذه المشكلة نستخدم الحقائق المعروفة لنا من نظرية التكاملات وهي:

مساحة القطاع المنحني.

ضع في اعتبارك بعض الدالة r = r (ϕ) المحددة في [α ، β].

ϕ 0 ∈ [α ، β] تقابل r 0 = r (ϕ 0) ، وبالتالي النقطة M 0 (ϕ 0 ، r 0) ، حيث ϕ 0 ،

ص 0 - الإحداثيات القطبية للنقطة. إذا تغيرت ، "الركض عبر" الكل [α ، β] ، فإن النقطة المتغيرة M ستصف بعض المنحنى AB المعطى بواسطة

المعادلة ص = ص (ϕ).

التعريف 7.4. القطاع المنحني هو شكل يحده شعاعين ϕ = α و ϕ = β ومنحنى AB معطى في القطبية

إحداثيات بواسطة المعادلة r = r (ϕ) ، α ≤ ϕ ≤ β.

ما يلي

نظرية. إذا كانت الوظيفة r (ϕ)> 0 ومستمرة على [α ، β] ، فإن المنطقة

يتم حساب القطاع المنحني بالصيغة:

تم إثبات هذه النظرية في وقت سابق في موضوع تكامل محدد.

استنادًا إلى النظرية أعلاه ، فإن مشكلتنا في إيجاد مساحة الشكل الذي يحده قوس واحد من الدائرة الحلقية ، والمعادلة الخاصة بها معطاة بواسطة البارامترية x = a (t - sin t) ، y = a ( 1 - cos t) ، ويتم تقليل محور Ox إلى الحل التالي.

المحلول. من معادلة المنحنى dx = a (1 − cos t) dt. يتوافق القوس الأول للدوران مع التغيير في المعلمة t من 0 إلى 2π. بالتالي،

رقم المهمة 2. أوجد طول قوس واحد من الحلقة الدائرية

تمت دراسة النظرية التالية ونتيجتها الطبيعية في حساب التفاضل والتكامل.

نظرية. إذا تم إعطاء المنحنى AB بواسطة المعادلة y = f (x) ، حيث f (x) و f '(x) متصلتان ، فإن AB يكون قابلاً للتصحيح و

عاقبة. دعنا نحصل على AB بشكل حدودي

L AB = (1)

دع الدوال x (t) و y (t) قابلة للاشتقاق باستمرار في [α ، β]. ثم

الصيغة (1) يمكن كتابتها كـ

لنقم بتغيير المتغيرات في هذا التكامل x = x (t) ، ثم y '(x) = ؛

dx = x '(t) dt ومن ثم:

الآن دعنا نعود إلى حل مشكلتنا.

المحلول. لدينا وبالتالي

رقم المهمة 3. من الضروري إيجاد مساحة السطح S المتكونة من دوران قوس دائري واحد

L = ((x، y): x = a (t - sin t)، y = a (1 - cost)، 0≤ t ≤ 2π)

في حساب التفاضل والتكامل ، توجد الصيغة التالية لإيجاد مساحة سطح جسم ثورة حول المحور x لمنحنى معطى حدوديًا على قطعة: x = φ (t)، y = ψ (t) (t) 0 ≤t t 1)

بتطبيق هذه الصيغة على معادلة السيكلويد الخاصة بنا ، نحصل على:

رقم المهمة 4. أوجد حجم الجسم الذي تم الحصول عليه من خلال تدوير قوس الحلقة الدائرية

على طول محور الثور.

في حساب التفاضل والتكامل ، عند دراسة المجلدات ، هناك الملاحظة التالية:

إذا تم إعطاء المنحنى الذي يحيط شبه المنحني المنحني بواسطة المعادلات البارامترية وكانت الوظائف في هذه المعادلات تفي بشروط النظرية الخاصة بتغيير المتغير في تكامل معين ، فإن حجم جسم دوران شبه المنحرف حول محور الثور سوف تحسب بالصيغة

لنستخدم هذه الصيغة لإيجاد الحجم الذي نحتاجه.

تم حل المشكلة.

استنتاج

لذلك ، في سياق هذا العمل ، تم توضيح الخصائص الرئيسية للدوران الحلقي. تعلموا أيضًا كيفية بناء سيكلويد ، واكتشفوا المعنى الهندسي للدوراني. كما اتضح ، فإن cycloid له تطبيق عملي ضخم ليس فقط في الرياضيات ، ولكن أيضًا في الحسابات التكنولوجية ، في الفيزياء. لكن الدويري له مزايا أخرى. تم استخدامه من قبل علماء القرن السابع عشر في تطوير طرق لدراسة الخطوط المنحنية ، تلك الطرق التي أدت في النهاية إلى اختراع التفاضل والتكامل. كانت أيضًا واحدة من "المحاور" التي اختبر عليها نيوتن ولايبنيز وباحثوهم الأوائل قوة الأساليب الرياضية الجديدة القوية. أخيرًا ، أدت مشكلة الزمن الأقصر إلى اختراع حساب الاختلافات ، وهو أمر ضروري جدًا لعلماء الفيزياء اليوم. وهكذا ، كان الدويري مرتبطًا ارتباطًا وثيقًا بواحدة من أكثر الفترات إثارة في تاريخ الرياضيات.

المؤلفات

1. بيرمان ج. سيكلويد. - م ، 1980

2. Verov S.G. Brachistochrone ، أو سر آخر من cycloid // Kvant. - 1975. - رقم 5

3. Verov S.G. أسرار cycloid // Kvant. - 1975. - رقم 8.

4. Gavrilova R.M.، Govorukhina A.A.، Kartasheva L.V.، Kostetskaya G.S.، Radchenko T.N. تطبيقات لا يتجزأ محدد. إرشادات وواجبات فردية لطلاب السنة الأولى بكلية الفيزياء. - روستوف غير متوفر: UPL RSU، 1994.

5. Gindikin S.G. عمر النجم للدوران الحلقي // Kvant. - 1985. - رقم 6.

6. Fikhtengolts G.M. دورة حساب التفاضل والتكامل. T.1. - م ، 1969

هذا الخط يسمى "مغلف". كل خط منحني هو مظروف ظلماته.

المادة والحركة ، والطريقة التي تشكلانها ، تمكن الجميع من إدراك إمكاناتهم في معرفة الحقيقة. إن تطوير منهجية لتطوير شكل من أشكال التفكير الديالكتيكي المادي وإتقان طريقة إدراك مماثلة هي الخطوة الثانية نحو حل مشكلة التطور وإدراك إمكانيات الإنسان. جزء XX فرص ...

يمكن أن يمرض الموقف مع وهن عصبي - عصاب ، أساس الصورة السريرية له حالة وهن. يتجلى جوهر الحماية الروحية (النفسية) في كل من حالة الوهن العصبي وفي حالة عدم المعاوضة من الاعتلال النفسي الوهن العصبي ، من خلال الابتعاد عن الصعوبات إلى الضعف العصبي مع الاختلالات الخضرية: إما أن "يقاوم" الشخص دون وعي منه أكثر من هجوم ...

أنواع مختلفة من الأنشطة ؛ تطوير الخيال المكاني والتمثيلات المكانية والتفكير المجازي والمكاني والمنطقي والتجريدي لأطفال المدارس ؛ تكوين المهارات لتطبيق المعرفة والمهارات الهندسية والرسومات لحل المشكلات التطبيقية المختلفة ؛ التعرف على محتوى وتسلسل مراحل أنشطة المشروع في المجال الفني و ...

أقواس. اللوالب هي أيضًا ملتوية لمنحنيات مغلقة ، مثل مطوي الدائرة. يتم إعطاء أسماء بعض اللوالب من خلال تشابه معادلاتها القطبية مع معادلات المنحنيات في الإحداثيات الديكارتية ، على سبيل المثال: Parabolic spiral (a - r) 2 = bj ، الحلزوني الزائدي: r = a / j. Rod: r2 = a / j si-ci-spiral ، والتي تبدو معادلاتها البارامترية مثل: ،)