Inviare il tuo buon lavoro nella knowledge base è semplice. Usa il modulo sottostante
Gli studenti, i dottorandi, i giovani scienziati che utilizzano la base di conoscenze nei loro studi e nel loro lavoro ti saranno molto grati.
postato su http://www.allbest.ru/
Istituto d'Istruzione
"Pedagogico statale bielorusso
Università Maxim Tank
Facoltà di Fisica e Matematica
Dipartimento di Matematica e Metodi di Insegnamento della Matematica
CORSO DI LAVORO SUL TEMA
"CICLOIDE"
Minsk, 2016
pendolo tautocrono ad arco cicloide
- introduzione
- 1. Proprietà di base della cicloide
- 2. Definizione geometrica di una cicloide
- 3. Area dell'arco della cicloide
- 4. Lunghezza dell'arco dell'arco cicloide
- 5. Il volume del corpo ottenuto ruotando l'arco della cicloide
- 6. Il miglior pendolo
- Conclusione
- Bibliografia
INTRODUZIONE
L'argomento del mio corso di lavoro è la cicloide. Questa curva è notevole in molti modi. È anche la traccia della punta del cerchione della ruota che rotola, è anche la curva delle oscillazioni di un periodo costante, è anche la curva della discesa più veloce. Al giorno d'oggi, le curve cicloidali sono utilizzate in molti calcoli tecnici e la conoscenza di queste curve facilita lo studio delle parti della macchina. Senza entrare nei dettagli, ricordiamo che le proprietà delle curve cicloidali sono utilizzate nella costruzione dei profili dei denti degli ingranaggi e in molte altre questioni tecniche. Anche da un punto di vista puramente applicativo, queste curve meritano la più seria attenzione. Pertanto, ho considerato questo argomento rilevante e interessante da studiare.
Quali problemi sorgono nello studio della cicloide? Innanzitutto è necessario dargli una definizione puramente geometrica, indipendente dalla meccanica. Successivamente, è necessario studiarne le proprietà, considerare la tangente, calcolare l'area delimitata dall'arco della cicloide e la sua base, la lunghezza dell'arco, il volume del corpo formato dalla rotazione dell'arco della cicloide attorno al orientamento.
Il lavoro del corso considererà in dettaglio la proprietà tautocrona della cicloide e la sua applicazione per creare il miglior pendolo. L'importanza degli orologi a pendolo non può essere sottovalutata, poiché fino a poco tempo fa erano gli orologi più precisi che garantivano il servizio del tempo negli osservatori astronomici.
Un altro merito della cicloide, che va notato, è che è stato utilizzato dagli scienziati nello sviluppo di metodi per lo studio delle linee curve, che hanno portato all'invenzione del calcolo differenziale e integrale. Nel mio lavoro, propongo di confrontare il calcolo della lunghezza dell'arco dell'arco cicloide, la superficie sotto l'arco e i volumi dei corpi formati dalla rotazione dell'arco cicloide prima dell'avvento del calcolo integrale, lungo e non sempre assolutamente rigoroso e utilizzando l'integrazione.
Obbiettivo: studio di materiale sull'argomento "cicloide"; studio delle caratteristiche del miglior pendolo; confronto dello studio delle linee curve prima e dopo la comparsa del calcolo integrale, calcolo della lunghezza dell'arco dell'arco cicloide, della superficie sotto l'arco e dei volumi dei corpi formati dalla rotazione dell'arco cicloide.
1. PRINCIPALI PROPRIETA' DELLA CICLODIA
Per prima cosa devi scoprire che tipo di curva è chiamata cicloide.
Considera un cerchio di raggio un centrato nel punto A. Lascia che il cerchio in questione rotoli senza scivolare lungo l'asse OX. Viene chiamata una curva descritta da un punto qualsiasi della circonferenza cicloide.
Questa definizione della cicloide non ha mai soddisfatto gli scienziati: dopotutto, si basa su concetti meccanici: velocità, addizioni di movimenti, ecc. Pertanto, i geometri hanno sempre cercato di dare alla cicloide una "definizione puramente geometrica". tale definizione, devi prima di tutto studiare le proprietà di base della cicloide, usando la sua definizione meccanica. Scegliendo la più semplice e caratteristica di queste proprietà, possiamo usarla come base per una definizione geometrica.
Iniziamo studiando la tangente e la normale alla cicloide. Che cosa tangente a una linea storta, tutti immaginano abbastanza chiaramente; pertanto non lo presenteremo qui. normale detta perpendicolare alla tangente, restaurata nel punto di contatto. Sulla fig. 1.1 mostra la tangente e la normale alla curva AB nel suo punto M.
Si consideri una cicloide (Fig. 1.2). Il cerchio rotola in una linea retta AB. Assumiamo che il raggio verticale del cerchio, che nel momento iniziale passava per il punto più basso della cicloide, riesca a girare di un angolo χ e assuma la posizione OM. In altre parole, riteniamo che il segmento M o T sia una tale frazione del segmento M o M 1 che l'angolo q sia da un giro completo. In questo caso, il punto M 0 è arrivato al punto M.
Il punto M è il punto della cicloide che ci interessa.
Freccia Oh rappresenta la velocità del centro del cerchio di rotolamento. Tutti i punti del cerchio, compreso il punto M, hanno la stessa velocità orizzontale, ma in aggiunta il punto M partecipa alla rotazione del cerchio. La velocità MC, che il punto M del cerchio riceve durante questa rotazione, è diretta tangenzialmente SM 1 al cerchio, cioè perpendicolare al raggio OM. E da allora in questo caso, la velocità MS è uguale in grandezza alla velocità MP (cioè la velocità LUI). Pertanto, il parallelogramma delle velocità nel caso del nostro movimento sarà un rombo (il rombo del MSKR in Fig. 1.2). La diagonale MK di questo rombo ci darà solo una tangente alla cicloide.
Tutto quanto sopra permette di risolvere il seguente problema costruttivo: data la retta AB della cicloide, il raggio r della circonferenza generatrice, ed il punto M appartenente alla cicloide (Fig. 1.2). È necessario costruire una tangente del MK alla cicloide.
Avendo un punto M, possiamo facilmente costruire una circonferenza generatrice, nella sua posizione in cui il punto sulla circonferenza cade in M. Per fare ciò, troviamo prima il centro o usando un raggio MO= r (il punto O deve giacere su una retta parallela ad AB, a distanza r da esso). Quindi costruiamo un segmento MP di lunghezza arbitraria, parallelo alla linea guida. Quindi costruiamo una linea SM 1 , perpendicolare a OM. Su questa linea, ci fermiamo dal punto M segmento MC uguale a MP. Su MS e MP, come sui lati, costruiamo un rombo. La diagonale di questo rombo sarà la tangente alla cicloide nel punto M.
Questa costruzione è puramente geometrica, anche se l'abbiamo ottenuta utilizzando i concetti della meccanica. Ora possiamo dire addio ai meccanici e ottenere ulteriori conseguenze senza il suo aiuto. Cominciamo con un semplice teorema.
Teorema 1. Angolo tra tangente e cicloide (in un punto arbitrario) e la linea direttrice è uguale al complemento di 90° metà dell'angolo di rotazione del raggio del cerchio generatore.
In altre parole, in fig. 1.2
? KLT uguale a o
Dimostreremo ora questa uguaglianza. Per abbreviare il discorso, concorderemo di chiamare "angolo base" l'angolo φ di rotazione del raggio del cerchio generatore. Ciò significa che l'angolo MOT in Fig. 1.2 - l'angolo principale. Assumiamo che l'angolo principale sia acuto. Nel caso in cui il cerchio di rotolamento compia più di un quarto di giro completo, la dimostrazione sarà simile.
Considera l'angolo CMP. Il lato CM è perpendicolare OM(la tangente alla circonferenza è perpendicolare al raggio). Lato MP (orizzontale) perpendicolare a DA(verso la verticale). Ma l'angolo MOP, per condizione, è acuto e l'angolo CMP è ottuso. Quindi gli angoli ILO e SMR sommare fino a 180° (angoli con lati tra loro perpendicolari, di cui uno acuto e l'altro ottuso).
Quindi, l'angolo CMP è uguale a 180° -ts. Ma, come sai, la diagonale di un rombo taglia in due l'angolo al vertice. Pertanto, Ugo
KMR = 90° -,
QED
Rivolgiamo ora la nostra attenzione alla normale alla cicloide. Rappresentiamo il lato sinistro della Fig. 1.2 è più grande e disegniamo una normale ME (ME ? MK; Riso. 1.3).
Dalla fig. 1.3 ne consegue che l'angolo EMP è uguale alla differenza degli angoli KME e KMR, cioè. è uguale a 90° - ? KMP.
Ma abbiamo appena dimostrato che l'angolo stesso KMRè uguale a 90° -
Quindi, otteniamo:
? RME= 90° - ? KMR= 90° - (90° -) =
Abbiamo dimostrato un teorema semplice ma utile. Formuliamolo:
Teorema 2. Angolo tra la normale alla cicloide (in qualsiasi momento) e la linea guida è uguale alla metà dell '"angolo principale".
Colleghiamo il "punto (T) della circonferenza generatrice ora il punto M (il "punto attuale" della cicloide) con il "inferiore (con il punto di contatto della circonferenza generatrice e la retta - Fig. 1.3) . Il triangolo MOT è ovviamente isoscele (OM e DA sono i raggi del cerchio generatore). La somma degli angoli alla base di questo triangolo è uguale a 180 ° - u, e ciascuno degli angoli alla base è un tappeto di questa somma. Così, ? OMT= 90° - .
Presta attenzione all'angolo RMT.È uguale alla differenza angolare HTA e OMR. Ora l'abbiamo visto ? OMT pari a 90° - ; per quanto riguarda l'angolo OMP, non è difficile scoprire a cosa corrisponda. Dopotutto, l'angolo OMR uguale all'angolo DOM(angoli trasversali interni quando paralleli).
Lo è subito evidente ? DOM pari a 90° - c. Significa, ? OMP= = 90° - c. Quindi, otteniamo:
RMT = ? HTA - ? OMR \u003d 90 ° - - (90 ° - c) \u003d.
Si scopre un risultato meraviglioso: l'angolo RMT risulta essere uguale all'angolo PME (per il Teorema 2). Pertanto, ME diretto e MT si fonderanno! Il nostro riso 1.3 non è fatto proprio bene! La corretta disposizione delle linee è data in fig. 1.4.
Formuliamo il risultato ottenuto nella forma del Teorema 3.
Teorema 3 (la prima proprietà principale della cicloide). La normale alla cicloide passa per il punto "inferiore" del cerchio generatore.
Questo teorema ha un semplice corollario. L'angolo tra una tangente e una normale è, per definizione, un angolo retto. Questo è l'angolo inscritto nella circonferenza del cerchio generatore. Pertanto, deve essere basato sul diametro del cerchio. Così, TT 1 -- diametro, e T 1 -- punto "superiore" del cerchio generatore. Formuliamo il risultato ottenuto.
Conseguenza (la seconda proprietà principale della cicloide). La tangente alla cicloide passa per il punto "superiore" del cerchio generatore.
Per spiegare questa proprietà, dobbiamo costruire una cicloide.
La costruzione della cicloide viene eseguita nella seguente sequenza:
1. Sulla linea orizzontale di guida è posato un segmento AA 12, pari alla lunghezza del cerchio generatore di raggio r, (2pr);
2. Costruire una circonferenza generatrice di raggio r, in modo che la retta sia tangente ad essa nel punto A;
3. Il cerchio e il segmento AA 12 sono divisi in più parti uguali, ad esempio 12;
4. Dai punti di divisione 1 1 , 2 1 , ...12 1 ripristinare le perpendicolari all'intersezione con la continuazione dell'asse orizzontale della circonferenza nei punti 0 1 , 0 2 , ...0 12 ;
5. Dai punti di divisione del cerchio 1, 2, ... 12 vengono tracciate linee rette orizzontali, su cui sono realizzati serif con archi di un cerchio di raggio r;
6. I punti ottenuti A 1 , A 2 , ... A 12 appartengono alla cicloide.
Sulla fig. 1.6 la base della cicloide è divisa in 6 parti uguali;
Maggiore è il numero di divisioni, più accurato sarà il disegno. In ogni punto della cicloide da noi costruita, disegniamo una tangente, collegando il punto della curva con il punto "superiore" del cerchio generatore. Nel nostro disegno, abbiamo sette tangenti (due delle quali sono verticali). Ora disegnando a mano la cicloide, ci occuperemo che tocchi davvero ciascuna di queste tangenti: questo aumenterà notevolmente la precisione del disegno. In questo caso, la stessa cicloide girerà attorno a tutte queste tangenti).
Eseguiamo sullo stesso fico. 1,6 normali in tutti i punti trovati della cicloide. In totale ci saranno cinque normali, senza contare la guida. È possibile costruire a mano l'involucro di queste normali. Se invece di sei prendessimo 12 o 16 punti di divisione, allora ci sarebbero più normali nel disegno e la busta sarebbe delineata più chiaramente. Tale involucro di tutte le normali gioca un ruolo importante nello studio delle proprietà di qualsiasi linea curva. Nel caso di una cicloide si scopre un fatto curioso: l'involucro delle normali della cicloide è esattamente la stessa cicloide, spostata solo di 2 un giù e avanti RA A destra. Questo fatto è caratteristico della cicloide.
2. DEFINIZIONE GEOMETRICA DI UNA CICLODIA
Diamo ora una definizione della cicloide come luogo dei punti senza usare la meccanica. È più facile farlo. Considera una linea arbitraria AB(considereremo condizionatamente la sua direzione orizzontale) e un punto su di essa M 0 . Quindi, considera tutti i possibili cerchi di un certo raggio che sono tangenti a questa linea e situati su un lato di essa. Su ogni cerchio dal punto T toccandolo con una linea retta AB mettere da parte (in direzione del punto M 0 ) arco tm, uguale in lunghezza al segmento M 0 T. Luogo dei punti M(adottato su tutti i cerchi che abbiamo menzionato) e sarà un cicloide.
Stabiliamo un'altra importante proprietà della cicloide e cerchiamo di usarla come base per lo studio di questa curva.
Considera un triangolo MTT 1 (Fig. 2.1), formato dal diametro verticale del cerchio generatore, tangente alla cicloide e normale ad essa.
Angolo mt 1 T, come inscritto in una circonferenza, è uguale alla metà dell'angolo centrale basato sullo stesso arco, cioè uguale a. Spendiamo MK||AB e ME?AB. Il segmento ME svolgerà un ruolo significativo in futuro, quindi gli daremo un nome e una designazione: lo chiameremo "altezza" del punto M della cicloide e lo indicheremo con la lettera h. Quindi l'altezza del punto M le cicloidi sono la sua distanza dalla linea direttrice.
Prestiamo attenzione all'angolo KMT. È uguale all'angolo mt 1 T. Da un triangolo TMT 1 noi abbiamo:
MT = 2 unpeccato e dal triangolo TKM:
CT = MT sin.
Confrontando questi risultati e notando che CT = h, otteniamo infine:
h = 2 un peccato 2.
Abbiamo espresso l'altezza del punto M in termini di angolo tra la tangente al punto M e la verticale (consideriamo ancora orizzontale la direzione della retta AB). Ora esprimiamo il seno di questo angolo in termini di "altezza". Otteniamo, ovviamente:
dove attraverso K viene indicato il valore costante per la data cicloide . Enunciamo il risultato ottenuto nel teorema.
Teorema 4. Il seno dell'angolo tra la tangente alla cicloide nel punto M e la verticale è proporzionale alla radice quadrata dell'"altezza" del punto M.
Ovviamente, qualsiasi cicloide possiede questa proprietà. Sorge la domanda: in che misura questa proprietà caratterizza esattamente la cicloide: ogni curva che possiede questa proprietà sarà necessariamente una cicloide? Si può dimostrare che questo sarà il caso, -- che vale anche il seguente teorema (inverso):
Teorema 5. Data una retta AB e un punto M, allora l'unica curva che soddisfa le condizioni del Teorema 4 e passa per il punto M è una cicloide.
Inoltre, il raggio del cerchio generatore di questa cicloide è correlato al coefficiente K, che è menzionato nel Teorema 4, dalla seguente relazione:.
Vale anche la pena prestare attenzione a un'altra curva notevole, che si chiama compagno della cicloide.
Si consideri una cicloide (Figura 2.2). Dal suo punto M abbassiamo la perpendicolare al diametro verticale del cerchio generatore. Otteniamo il punto P. Eseguiamo questa costruzione per tutti i punti della cicloide senza eccezioni.
Quindi il punto P descriverà una certa curva. Questa curva è chiamata la compagna della cicloide.
Si consideri una cicloide, un punto M su di essa e il corrispondente punto P sul satellite (Fig. 2.3) Il centro del cerchio generatore sarà indicato dalla lettera Q. Allora avremo:
QP=QM cos?MQP= un cos(180 0 -ts)=- un cosè=- un sin(90 0 -ts)= un peccato(c -90 0).
Tracciamo il luogo dei centri del cerchio generatore (linea retta XX 1 ). dal punto M 0 rimandare AB segmento M 0 K, uguale. Spendiamo KY ? XX 1 . Il punto di intersezione di queste linee sarà indicato dalla lettera o. Segmento M 0 R sulla retta direttrice dalla punta della cicloide al punto di contatto della circonferenza generatrice è uguale a un c, dove c è l'angolo principale MQR, espresso in radianti. Segmento OQ sull'asse orizzontale XX 1 è uguale a M 0 R - M 0 K=un(c -) e il segmento QPè uguale a un peccato? PMQ, cioè uguale al seno dell'angolo (c -), moltiplicato per il raggio un.
Quindi dal punto o orizzontalmente vengono tracciati segmenti di lunghezza uguale agli archi di cerchio e lungo le linee verticali dei seni degli angoli corrispondenti a questi archi. Questa è la costruzione di una normale sinusoide a noi nota.
Significa, La compagna di una cicloide è chiamata sinusoide.
Non approfondiremo lo studio delle proprietà di questa curva davvero notevole, lo noteremo solo come dato di fatto l'area delimitata dal compagno di un arco della cicloide e la sua base è pari al doppio dell'area del cerchio generatore.
3. PIAZZA DELL'ARCO DELLA CICLODIA
La prima menzione del calcolo dell'area racchiusa tra l'arco della cicloide e la sua base è nelle opere del Viviani e del Torricelli. Allo stesso tempo, usavano una tecnica speciale, chiamata il "metodo degli indivisibili". Questo metodo consiste nel dividere una figura curvilinea in strisce infinitamente sottili, la cui area è relativamente facile da trovare, e quindi si sommano queste aree. Questa tecnica portò alla comparsa del calcolo integrale mezzo secolo dopo.
Si consideri una figura delimitata da un arco cicloide e da una sinusoide. Nella figura 3.1, questa figura, composta da due petali, è cerchiata con una linea spessa. Calcoliamo la sua area.
Prima di tutto, costruiamo un'immagine speculare del petalo destro della figura rispetto alla retta direttrice AB (questa riflessione è data in Figura 4.1 da una linea tratteggiata). Spostiamo quindi questa curva tratteggiata verso l'alto a sinistra e applichiamola al petalo sinistro in modo che gli archi delle sinusoidi compresi nel contorno di ciascuno dei petali coincidano. Otteniamo una figura convessa, ombreggiata in figura 3.1 e rappresentata separatamente in fig. 3.2. Questa figura è chiamata la figura di Roberval. Stabiliamo le proprietà più importanti di questa figura.
1. La figura convessa M 0 RLM è di dimensioni uguali alla figura a due petali rappresentata dalla linea spessa in Fig. 3.1. Questo si può vedere dal fatto che è "composto" dagli stessi petali.
2. Qualsiasi corda orizzontale di una figura convessa è uguale al doppio della corda di un petalo alla stessa distanza da AB. Infatti le corde CE e PH (Fig. 3.1) del petalo destro, equidistanti dal cerchio generatore, sono ugualmente distanti dal centro. Quindi CT \u003d CE \u003d PH \u003d P 1 H 1 \u003d TL.
Questo dà un risultato importante: la corda MR di una figura convessa (Fig. 3.2) è uguale alla corda della circonferenza generatrice SK, posta alla stessa distanza dalla retta.
Consideriamo ora la figura convessa di Roberval e la circonferenza tangente alle stesse rette AB e A 1 B 1, e colleghiamo i punti della loro intersezione con la circonferenza e con il contorno della figura convessa in successione per segmenti di retta, come mostrato in figura. I poligoni inscritti così ottenuti (HLMNPQRSTK e H 1 L 1 M 1 N 1 P 1 Q 1 R 1 S 1 T 1 K 1) saranno detti poligoni "corrispondenti" su una serie di trapezi (e triangoli). Le aree dei trapezi "corrispondenti" nel cerchio e nella figura di Robervel, ad esempio NPRS e N 1 P 1 R 1 S 1, sono uguali, perché questi trapezi, rispettivamente, hanno le stesse basi inferiori, basi superiori (corrispondenti accordi) e altezze. Sulla fig. 3.2 trapezi corrispondenti di uguali dimensioni sono ricoperti con lo stesso tratteggio.
Ora aumenteremo indefinitamente il numero di rette "intermedie" parallele ad AB, in modo che la distanza tra ogni coppia vicina tenda a zero. Quindi in un cerchio otteniamo una serie di poligoni inscritti, il cui numero di lati aumenta indefinitamente e ciascuno dei lati tende a zero. Sappiamo che le aree S n di questi poligoni sono limitate dall'area di un cerchio:
lim S n= p un 2 .
Come si comporterà in questo caso la sequenza di poligoni inscritti in una figura di Roberval convessa? Piazza? n poligoni inscritti consecutivi tenderanno ad area? figure di Roberval. È noto che se due variabili mantengono valori corrispondentemente uguali per tutte le loro modifiche e una di esse tende a un certo limite, l'altra tende allo stesso limite. Ma ogni poligono inscritto nella figura di Roberval è di dimensioni uguali al corrispondente poligono inscritto nel cerchio. Concludiamo quindi che il limite delle aree dei poligoni inscritti in una figura di Roberval è uguale al limite delle aree dei corrispondenti poligoni inscritti in un cerchio; il che significa che l'area della figura convessa di Roberval è uguale all'area del cerchio generatore:
Da ciò otteniamo una conseguenza immediata: l'area della figura a due petali è uguale all'area del cerchio generatore.
Diamo ora un'occhiata alla Figura 3.1. L'area della figura AOTPBKA, come abbiamo visto, è pari al doppio dell'area del cerchio generatore. Abbiamo appena determinato l'area della figura a due petali: è uguale all'area del cerchio generatore. Di conseguenza, l'area delimitata dall'arco della cicloide e dalla sua base è pari a tre volte l'area del cerchio generatore.
Ora troviamo l'area racchiusa tra l'arco della cicloide e la sua base usando la geometria differenziale.
Dove t? .
Troviamo la derivata
4. LUNGHEZZA DELL'ARCO DEL CICLOIDE
La lunghezza dell'arco di una cicloide fu calcolata per la prima volta dall'architetto e matematico inglese Wren nel 1658. Wren procedeva da considerazioni meccaniche che ricordavano i primi lavori di Torricelli e Roberval. Ha considerato la rotazione di un cerchio di rotolamento di un angolo molto piccolo vicino al punto "inferiore" del cerchio generatore. Per dare forza probatoria alle suggestive considerazioni di Wren, si dovrebbe considerare un certo numero di teoremi ausiliari, e di conseguenza si dovrebbe spendere troppo lavoro.
È molto più conveniente utilizzare un percorso più lungo, ma più delicato. Per fare ciò, devi considerare una curva speciale che ha ogni curva piatta: il suo sweep.
Si consideri un arco convesso AB di una linea curva (Fig. 4.1). Immaginiamo che un filo inestensibile flessibile della stessa lunghezza dell'arco AB stesso sia attaccato all'arco AB nel punto A, e questo filo sia "avvolto" sulla curva e lo confina strettamente, in modo che la sua estremità coincida con il punto B Si “srotolerà” - raddrizziamo il filo tenendolo teso, in modo che la parte libera del filo CM sia sempre diretta tangenzialmente all'arco AB. In queste condizioni, la fine del thread descriverà una certa curva. È questa curva che si chiama sweep, o, in latino, evolvente curva originale.
Se l'arco della curva non è ovunque convesso in una direzione, se esso, come la curva AB in Fig. 4.2 ha un punto C in cui la tangente alla curva passa da un lato all'altro (tale punto si chiama punto di flesso), quindi in questo caso si può parlare anche dello sviluppo della curva, ma il ragionamento avrà essere un po' più complicato.
Immagina che il filo sia fissato proprio nel punto di flesso C (Fig. 4.2). Il filo, che si avvolge dall'arco BC, descriverà la curva BMP: uno sweep.
Immagina ora un filo avvolto attorno all'arco AC della curva originale, ma questo filo è già allungato: nel punto C, ad esso è attaccato un pezzo di filo CP. Avvolgendo il filo ACP allungato con la curva SA, otteniamo un arco di RNA che, insieme all'arco BMP, forma un'unica curva continua - continua, ma non ovunque liscia: il punto di deflessione C della curva originale corrisponderà alla punta (punto di ritorno) della curva VMRNA: la curva VMRNA sarà l'evolvente (sweep) della curva ICA.
Questi esempi ci hanno aiutato ad abituarci ai nuovi concetti di evoluto ed evolvente. Ora studiamo lo sviluppo delle curve cicloidali.
Studiando questa o quella curva, abbiamo spesso costruito una curva ausiliaria - un "compagno" di questa curva. Quindi, ci costa una sinusoide, una compagna di una cicloide. Ora, partendo dalla cicloide data, costruiamo una cicloide ausiliaria indissolubilmente legata ad essa. Si scopre che lo studio congiunto di una tale coppia di cicloidi è per alcuni aspetti più facile dello studio di una singola cicloide. Chiameremo tale cicloide ausiliario cicloide di accompagnamento.
Considera metà dell'arco della cicloide AMB (Fig. 4.3). Non dovremmo essere imbarazzati dal fatto che questa cicloide si trovi in un modo insolito ("capovolto"). Tracciamo 4 linee parallele alla linea direttrice AK a distanze un, 2un, 3un e 4 un. Costruiamo un cerchio generatore nella posizione corrispondente al punto M (in Fig. 4.3 il centro di questo cerchio è indicato dalla lettera O). L'angolo di rotazione di MON sarà indicato con c. Allora il segmento AN sarà uguale a bc (l'angolo u è espresso in radianti).
Continuiamo il diametro HT della circonferenza generatrice oltre il punto T fino all'intersezione (nel punto E) con la retta PP. Su TE come diametro, costruiamo un cerchio (con centro O 1). Costruiamo una tangente nel punto M alla cicloide AMB. Per fare ciò, il punto M deve, come sappiamo, essere connesso al punto T. Continuiamo la tangente MT oltre il punto T fino all'intersezione con la circonferenza ausiliaria, e chiameremo il punto di intersezione M 1. È questo il punto M 1 che vogliamo ora affrontare.
Abbiamo indicato l'angolo MON con c. Pertanto, l'angolo MTH sarà uguale a (angolo inscritto basato sullo stesso arco). Triangolo TO 1 M 1, ovviamente, isoscele. Pertanto, non solo l'angolo O 1 TM 1, ma anche l'angolo TM 1 O 1 saranno ciascuno uguale. Pertanto, la quota dell'angolo TO 1 M 1 nel triangolo TO 1 M 1 rimane esattamente p - q radianti (ricordiamo che l'angolo 180? è uguale a p radianti). Notiamo anche che il segmento NK è ovviamente uguale a b (p - c).
Consideriamo ora un cerchio con centro O 2, mostrato in Figura 4.3 da una linea tratteggiata. Dal disegno è chiaro di che tipo di cerchio si tratta. Se lo fai rotolare senza scivolare lungo la linea retta CB, il suo punto B descriverà la cicloide BB. Quando il cerchio tratteggiato ruota per l'angolo p - c, il centro O 2 arriverà al punto O 1 e il raggio O 2 B assumerà la posizione O 1 M 1. Pertanto, il punto M 1 da noi costruito risulta essere un punto della cicloide BB.
La costruzione descritta assegna a ciascun punto M della cicloide AMB un punto M 1 della cicloide VM 1 B. In fig. 4.4 questa corrispondenza è mostrata più chiaramente. La cicloide ottenuta in questo modo è chiamata cicloide di accompagnamento. Sulla fig. 4.3 e 4.4, le cicloidi rappresentate da linee tratteggiate in grassetto si accompagnano rispetto alle cicloidi rappresentate da linee continue in grassetto.
Dalla fig. 4.3 si può vedere che la linea MM 1 è la normale nel punto M 1 alla cicloide di accompagnamento. Tale retta passa infatti per il punto M 1 della cicloide e per il punto T di tangenza tra la circonferenza generatrice e la retta direttrice (il punto "più basso" della circonferenza generatrice, come si diceva; ora risultava essere "più alto", perché il disegno è ruotato). Ma questa stessa linea, per costruzione, è tangente alla "base" della cicloide AMB. Pertanto, la cicloide originale tocca ogni normale della cicloide di accompagnamento. È l'involucro per le normali della cicloide di accompagnamento, cioè la sua evoluzione. E la cicloide "di accompagnamento" risulta essere semplicemente un'evolvente della cicloide originale!
In questa costruzione ingombrante ma essenzialmente semplice, abbiamo dimostrato un notevole teorema scoperto dallo scienziato olandese Huygens. Ecco il teorema: l'evoluzione di una cicloide è esattamente la stessa cicloide, solo spostata.
Avendo costruito un evoluto non per un arco, ma per l'intera cicloide (che, ovviamente, può essere fatto solo mentalmente), quindi un evoluto per questo evoluto, ecc., otteniamo Fig. 4.5, simile a tessere.
Prestiamo attenzione al fatto che per dimostrare il teorema di Huygens non abbiamo utilizzato stime né infinitesime, né indivisibili, né approssimate. Non usavamo nemmeno la meccanica, anche se a volte usavamo espressioni mutuate dalla meccanica. Questa prova è tutta nello spirito del ragionamento utilizzato dagli scienziati del Seicento quando hanno voluto motivare rigorosamente i risultati ottenuti con l'ausilio di varie considerazioni suggestive.
Un importante corollario segue immediatamente dal teorema di Huygens. Consideriamo il segmento AB di Fig. 4.4. La lunghezza di questo segmento è ovviamente pari a 4 un. Immagina ora che un filo sia avvolto sull'arco della cicloide AMB, fissato nel punto A e dotato di una matita nel punto B. Se "avvolgiamo" il filo, la matita si sposterà lungo lo sviluppo della cicloide AMB, ad es. lungo la cicloide BM 1 B. La lunghezza del filo, pari alla lunghezza del semiarco della cicloide, sarà ovviamente uguale al segmento AB, cioè, come abbiamo visto, 4 un. Pertanto, la lunghezza L dell'intero arco della cicloide sarà pari a 8 un e formula L=8 un può ora essere considerato sufficientemente rigorosamente provato.
Calcoliamo la lunghezza dell'arco usando la geometria differenziale. La soluzione così ottenuta sarà molto più breve e semplice:
dove t?
r(t)=
=
| r(t)|===2peccato
5. VOLUME DEL CORPO OTTENUTO DALLA ROTAZIONE DELL'ARCO DEL CICLOIDE
Troviamo il volume del corpo generato dalla rotazione dell'arco cicloide attorno alla sua base. Roberval lo trovò rompendo il risultante corpo a forma di uovo (Fig. 5.1) in strati infinitamente sottili, inscrivendo cilindri in questi strati e sommando i loro volumi. La dimostrazione è lunga, noiosa e non del tutto rigorosa. Pertanto, per calcolarlo, ci rivolgiamo alla matematica superiore. Impostiamo parametricamente l'equazione cicloide.
Nel calcolo integrale, quando studia i volumi, usa la seguente osservazione:
Se la curva che delimita il trapezio curvilineo è data da equazioni parametriche e le funzioni in queste equazioni soddisfano le condizioni del teorema sul cambiamento di variabile in un certo integrale, allora il volume del corpo di rotazione del trapezio attorno all'asse Ox sarà essere calcolato con la formula:
Usiamo questa formula per trovare il volume di cui abbiamo bisogno.
Allo stesso modo, calcoliamo la superficie di questo corpo.
L=((x,y): x=a(t - sin t), y=a(1 - costo), 0 ? t ? 2ð)
Nel calcolo integrale, esiste la seguente formula per trovare l'area della superficie di un corpo di rivoluzione attorno all'asse x di una curva specificata su un segmento parametricamente (t 0 ?t ?t 1):
Applicando questa formula alla nostra equazione cicloide, otteniamo:
Consideriamo anche un'altra superficie generata dalla rotazione dell'arco cicloide. Per fare ciò, costruiremo un'immagine speculare dell'arco cicloide rispetto alla sua base e ruoteremo la figura ovale formata dalla cicloide e la sua riflessione attorno all'asse KT (Fig. 5.2)
Per prima cosa, troviamo il volume del corpo formato dalla rotazione dell'arco cicloide attorno all'asse KT. Il suo volume sarà calcolato con la formula (*):
Pertanto, abbiamo calcolato il volume della metà di questo corpo di rapa. Quindi il volume totale sarà
Per trovare la superficie di questo corpo di rivoluzione usando l'integrale, è anche necessario dividerlo a metà orizzontalmente e considerare la sua parte superiore.
Quindi la superficie del corpo risultante è
6. IL MIGLIOR PENDOLO
Guardando il lampadario oscillante nel tempio, Galileo scoprì che il tempo del pieno svolgimento del lampadario, cioè il tempo trascorso il quale tornerà nella sua posizione originaria (c.d periodo di oscillazione), era lo stesso sia per campate grandi che piccole. Questa osservazione portò Galileo a pensare che un corpo oscillante (un pendolo) potesse essere utilizzato per controllare il funzionamento di un orologio.
Lo stesso Galileo non riuscì a realizzare un orologio a pendolo e presto divenne chiaro che le sue osservazioni erano imprecise. Osservazioni più accurate hanno mostrato che il periodo di oscillazione del pendolo è tanto maggiore quanto maggiore è l'oscillazione; ma a causa dell'inevitabile attrito dell'asse e della resistenza dell'aria, l'oscillazione di un pendolo ordinario diminuisce costantemente, il che significa che anche il periodo della sua oscillazione diminuirà. Orologio con pendolo ordinario - altrimenti chiamato pendolo circolare(perché ogni punto di esso descrive un arco di cerchio) non può andare correttamente.
Huygens ha scoperto come realizzare un pendolo circolare in modo che abbia un'oscillazione costante. Ma ha anche risolto un altro problema interessante: ha risposto alla domanda su quale curva dovrebbe muoversi il punto in modo che il periodo delle sue oscillazioni non dipenda dall'ampiezza. Ha escogitato un disegno che spostava il baricentro del pendolo lungo questa curva.
Partiamo da un dispositivo che assicura il corretto movimento di un orologio a pendolo circolare. Ingranaggio MA(Fig. 6.1) essere azionati da una catena con un peso A alla fine. Un ingranaggio è montato sull'asse di questa ruota, strettamente collegato ad esso. Questo ingranaggio aziona le lancette dell'orologio, e quindi è necessario che il volante MA spostato in modo uniforme.
Ma il peso A, come qualsiasi corpo, sotto l'influenza della gravità si muoverà accelerato, impartendo una rotazione accelerata alla ruota MA. Il pendolo dovrebbe eliminare la difficoltà MM.
Ancora DA giacente nel piano della ruota MA, strettamente connesso al pendolo MM, MM pendolo stesso si trova dietro il piano del disegno e quindi è disegnato con una linea tratteggiata. Ancora dotata di denti H e Per.
Al momento mostrato in Fig. 6.1 ruota MA tenuto dal polo sinistro H ancore DA. Quando il pendolo oscilla a sinistra, il polo H l'ancora rilascerà l'ingranaggio catturato della ruota e la ruota girerà, ma solo dal cingolato, perché l'ingranaggio Per le ancore cadranno nello spazio tra i denti della ruota e lo ritarderanno. Quando il pendolo oscillerà di nuovo a destra, il dente su quel lato sarà trattenuto dall'ancora. Quindi, ad ogni oscillazione completa del pendolo (avanti e indietro), la ruota girerà esattamente di un dente, ad es. ad una certa frazione del cerchio. Il movimento della ruota sarà rigorosamente uniforme. Denti di ancoraggio, come si vede dalla Fig. 6.1 sono tagliati obliquamente, in modo che il dente della ruota, trattenuto dall'ancora e nuovamente rilasciato, debba scorrere sulla superficie obliqua del dente dell'ancora. Di conseguenza, l'ancora darà una piccola spinta al pendolo. Queste spinte ritmiche compenseranno la perdita di energia che il pendolo consuma per superare l'attrito e la resistenza dell'aria. Pertanto, l'oscillazione del pendolo non diminuirà. Pertanto, il peso impartisce energia sia alle ruote dell'orologio che al pendolo stesso, mentre il pendolo regola il corso dell'orologio.
E se l'orologio si ferma? Non è difficile usarli: basta sollevare il peso e far oscillare il pendolo. Ma allo stesso tempo, l'oscillazione dell'oscillazione potrebbe risultare diversa e l'orologio andrà in modo uniforme, ma in modo errato (andrà avanti o inizierà a rimanere indietro). Huygens ha ideato un dispositivo che consente di regolare facilmente il corso dell'orologio. Ma Huygens, da vero scienziato, era interessato alla domanda: quale dovrebbe essere un pendolo "perfetto", un pendolo il cui tempo di oscillazione non dipende dall'entità dell'oscillazione? Consideriamo in dettaglio come Huygens ha risolto questo problema.
La parola "tautocrone" significa "uniforme". Così Huygens chiamò la curva, che cominciò a cercare, cioè una tale curva lungo la quale il baricentro del pendolo deve muoversi in modo che il periodo della sua oscillazione non dipenda dall'entità dell'oscillazione. La ricerca fu coronata da successo: il misterioso tautocrono si rivelò essere una cicloide poco studiata. In tal modo, Huygens ha mostrato uno spirito eccezionale. Basti dire che la dottrina degli evoluti è stata creata proprio nel processo di risoluzione di questo problema.
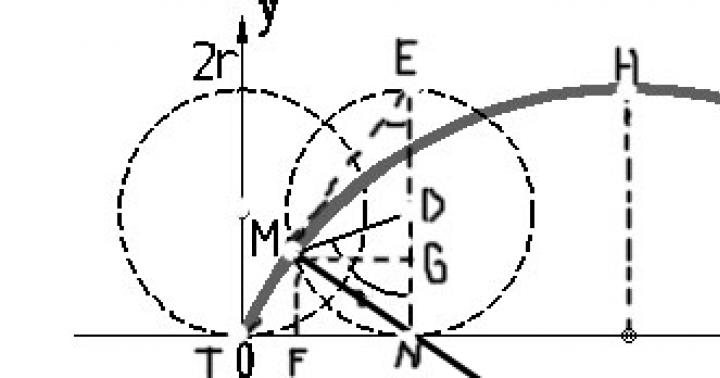
Huygens ragionava come segue. Immagina un solco a forma di cicloide, come mostrato in Fig. 6.2.
Una palla pesante rotola lungo questo solco M. Considereremo il caso ideale: il caso in cui non c'è attrito e resistenza dell'aria.
Indica i punti delle cuspidi della cicloide con M 0 e M? 0 , e il raggio del cerchio generatore passante un. Disegna un cerchio di raggio un tangente alla cicloide al vertice (cerchio centrato o) e generando un cerchio nella posizione corrispondente al punto M cicloidi (dati dalla linea tratteggiata). Diciamo che abbiamo messo la palla al punto M 1 scanalatura e lasciarlo andare senza una spinta. Sotto l'influenza della gravità, rotolerà verso il basso. Studiamo il suo movimento.
Quale sarà la velocità della palla quando raggiungerà il punto M cicloidi? È facile da calcolare. Discendente dal punto M 1 punto M, la palla consumerà un po' di energia potenziale. Questa perdita di energia è uguale al prodotto del peso della palla mg(m -- massa della palla, g-- accelerazione di gravità) a "perdita di quota", cioè sulla differenza di altezza della palla nelle posizioni M 1 e M, inoltre le altezze si misurano da un certo livello, ad esempio dal livello del suolo. Da qualunque livello si contano le altezze, la loro differenza nel nostro caso sarà uguale al segmento NM. Quindi, la potenziale perdita di energia della palla sarà uguale a mg· HM.
Ma in virtù della legge di conservazione dell'energia, l'energia potenziale perduta della palla si trasformerà nell'energia cinetica del suo movimento, che, come sapete, è uguale, se indichiamo la velocità ancora sconosciuta della palla. Uguagliando questa energia cinetica con l'energia potenziale persa, otteniamo l'equazione
da cui troviamo subito il valore della velocità desiderata
Anche la direzione di questa velocità è facile da determinare. Sarà diretto tangente alla cicloide, cioè lungo la corda ML(Fig. 6.2), dove l- il punto "più basso" del cerchio generatore.
Ci interesserà non tanto la velocità in sé quanto la sua proiezione verticale, ad es. "la velocità di discesa della palla", il tasso di variazione della sua altezza. Questa proiezione verticale è facile da calcolare: è uguale a, dove è l'angolo tra la corda ML e verticale. Accordo A cerchio con centro o, è ovviamente uguale e parallela alla corda ML, e quindi l'angolo LMP uguale all'angolo GATTO, che si nota in Fig. 6.2. Così:
Confronteremo il moto irregolare lungo una cicloide con il moto uniforme lungo una circonferenza. A tal fine, costruiamo un cerchio ausiliario come segue: attraverso il vertice MA la cicloide è disegnata perpendicolarmente ANNO DOMINI(diametro del cerchio con centro o), e attraverso il punto di partenza M 1 del movimento della palla, viene disegnato un parallelo M 1 B alla sua base. Sia indicato con la lettera il punto di intersezione di queste parallele e perpendicolari A. Il cerchio costruito AB, come sul diametro, e sarà il cerchio ausiliario desiderato. Non è ancora chiaro come sia meglio di altri circoli.
Iniziamo con il fatto che collegheremo la componente verticale della velocità della palla con gli elementi del cerchio ausiliario. Abbiamo:
perché NM = VC. Da un triangolo ATTO noi abbiamo:
Ma AT=2a cos , e quindi
Sostituiamo il valore del coseno trovato nell'espressione for SIG contrassegnati da un asterisco (*). Noi abbiamo:
L'ultima radice è uguale alla media proporzionale tra i segmenti VC e AK, cioè. tra i segmenti dell'ipotenusa AB triangolo ABC, in cui quest'ultimo è diviso per l'altezza SC. Ma questa media proporzionale, secondo il noto teorema delle rette proporzionali in un triangolo rettangolo, è esattamente uguale all'altezza SC:
VK·AK=SK 2 .
Pertanto, per la componente verticale SIG la velocità della pallina lungo la cicloide otteniamo infine:
MP=· KS.
Le quantità un e g datoci fin dall'inizio e non sono collegati con un punto M, né con la sua posizione iniziale M 1 . Pertanto, il movimento della palla lungo la cicloide è completamente determinato dalla corda KS cerchio ausiliario, cioè posizione del punto finale DA su questo cerchio.
Considera il moto uniforme di un punto DA lungo un cerchio ausiliario con una velocità angolare di radianti al secondo, cioè gradi al secondo. In questo caso, la velocità del punto DA lungo una circonferenza sarà uguale al prodotto del raggio della circonferenza e della velocità angolare, espressa in radianti (al secondo), cioè è uguale a
Quanto velocemente sta scendendo il punto? DA, Quanto velocemente cambia la sua distanza dalla retta? M 0 M? 0 con moto uniforme del punto DA intorno alla circonferenza? Questo è facile da calcolare.
Velocità il movimento di un punto del cerchio è diretto tangenzialmente al cerchio, cioè perpendicolare al raggio. La sua proiezione sulla verticale è uguale alla velocità stessa moltiplicato per il coseno dell'angolo Fig. 6.3. Ma l'angolo è ovviamente uguale all'angolo CSR 1: entrambi si ottengono sottraendo l'angolo o 1 CE da un angolo retto. Coseno di un angolo CSR 1 è uguale . Per la proiezione verticale della velocità di moto uniforme in un cerchio, troviamo:
Si ottiene un risultato notevole: quando un punto si muove uniformemente lungo un cerchio, la sua proiezione sulla verticale si muove esattamente allo stesso modo della proiezione sulla verticale di una palla che rotola lungo una cicloide. Le proiezioni di entrambe le velocità in qualsiasi momento sono uguali tra loro. Ma ne consegue che il punto del cerchio da A in MA e una palla su una cicloide di M 1 pollice MA arriverà nello stesso momento. Questa volta è facile da determinare. Abbiamo già detto che un punto sul cerchio ausiliario rende i radianti un secondo, in altre parole, trasformerà un radiante in secondi e i radianti in. Esattamente lo stesso tempo è necessario affinché la nostra palla rotoli giù dalla cicloide dal punto M 1 punto MA. Gli ci vorrà lo stesso tempo per salire per inerzia al punto M? 1 , lo stesso - per scendere di nuovo e lo stesso - per salire e tornare alla posizione di partenza (al punto M uno). Ciò significa che il tempo di piena oscillazione della sfera (periodo di oscillazione) sarà pari a:
Questa è una formula davvero meravigliosa. Vediamo che il periodo di movimento della pallina lungo il solco cicloide è completamente determinato dalle dimensioni del solco (il raggio del cerchio generatore della cicloide) e dall'accelerazione di gravità. Posizione del punto M 1 sulla cicloide, la sua distanza dalla retta M 0 M? 0 non importa. Da qualunque punto della cicloide la pallina inizi a muoversi, il periodo della sua oscillazione sarà lo stesso.
Huygens ha pensato a come utilizzare la proprietà tautocrona della cicloide per costruire un pendolo "perfetto". Come far muovere tautocronicamente la sfera del pendolo senza ricorrere a scanalature e dispositivi simili con molto attrito? Pensando a questo, Huygens è arrivato ai concetti di evoluto e involuto.
Realizziamo una sagoma composta da due semiarchi identici della cicloide aventi una cuspide comune o(Fig. 6.4). Indichiamo il raggio del cerchio generatore, come sempre, con un. Rafforzeremo il modello verticalmente e alla cuspide o legare un filo di lunghezza pari a 4 un-- cioè. il doppio del diametro del cerchio generatore della cicloide. filettatura libera T dagli una palla pesante.
La palla descriverà durante il suo movimento lo svolgersi della cicloide ASOEV, perché il thread si avvolgerà attorno al modello. Ma lo svolgimento della cicloide è esattamente la stessa cicloide. Quindi la curva VMTRA, lungo il quale si muove la pallina, sarà una cicloide generata da un cerchio di raggio un.
Se posizioniamo la palla in un punto arbitrario M e lasciarlo a se stesso, comincerà ad oscillare, e il periodo di queste oscillazioni non dipenderà dalla scelta del punto M. Anche se, sotto l'influenza dell'attrito e della resistenza dell'aria, l'oscillazione delle oscillazioni diminuisce, il tempo di oscillazione del pendolo rimane invariato. Davvero questo pendolo sarà tautocrono!
Consideriamo ora piccole oscillazioni del pendolo lungo l'arco AB cicloidi (Fig. 6.5). Se queste oscillazioni sono molto piccole, l'influenza della dima guida non sarà praticamente avvertita e il pendolo si muoverà quasi come un normale pendolo con una lunghezza l=4un, sospeso in un punto o. Sentiero AB il pendolo cicloidale non differirà praticamente dal percorso CE lunghezza del pendolo circolare 4 un. Ciò significa che il periodo di piccole oscillazioni di un normale pendolo circolare con una lunghezza l=4un non differirà praticamente dal periodo del pendolo cicloidale. Entrando nella formula
con cui ci siamo incontrati sopra, invece di un uguale ad esso, otteniamo l'espressione per il periodo di piccole oscillazioni di un pendolo circolare in termini di lunghezza:
CONCLUSIONE
Nel processo di completamento del mio corso di lavoro, ho studiato materiali sul tema della cicloide, studiato le caratteristiche del miglior pendolo, confrontato uno studio piuttosto elegante, ma non molto semplice, della cicloide prima dell'avvento del calcolo integrale, con il più semplice e molto familiare, studiato in geometria differenziale e analisi matematica; ancora una volta convinto della necessità di studiare queste discipline. Come si è scoperto, la cicloide ha un'enorme applicazione pratica non solo in matematica, ma anche nei calcoli tecnologici, in fisica.
Il lavoro sullo studio di questo argomento si è rivelato piuttosto eccitante e interessante.
BIBLIOGRAFIA
1. Berman G.N. Cicloide. -M., 2007. -113s.
2. Savelov A.A. Curve piatte. - M., 1960. - 293 pag.
3. Fikhtengolts G.M. Fondamenti di analisi matematica. -M., 2005, v.2. -464 pag.
Ospitato su Allbest.ru
...Documenti simili
Breve storia dello studio della cicloide. Definizione geometrica, proprietà e caratteristiche della costruzione della cicloide. Equazione cicloide parametrica ed equazione in coordinate cartesiane. Compiti per trovare parti di una cicloide e figure formate da una cicloide.
tesina, aggiunta il 16/01/2011
Momenti e centri di massa delle curve piane. Il teorema di Gulden. L'area della superficie formata dalla rotazione di un arco di una curva piana attorno ad un asse che giace nel piano dell'arco e non lo interseca è uguale al prodotto della lunghezza dell'arco per la lunghezza del cerchio.
lezione, aggiunta il 04/09/2003
Definizione di integrale definito, sue proprietà. La lunghezza dell'arco della curva. Area di un trapezio curvilineo. Superficie di rotazione. Aree di figure delimitate da grafici di funzioni delimitate da rette date da equazioni. Calcolo dei volumi dei corpi.
lavoro di controllo, aggiunto il 02/10/2017
Un integrale definito è un funzionale additivo normalizzato monotono definito su un insieme di coppie, suoi componenti, proprietà. Calcolo di un integrale definito; Formula di Newton-Leibniz. Applicazioni geometriche: area, lunghezza d'arco, volume di un corpo di rivoluzione.
presentazione, aggiunta il 30/05/2013
Trovare l'area di una figura delimitata da grafici di funzioni usando un doppio integrale. Ottenuto per rotazione del volume del corpo attorno all'asse OX della figura, limitato dalle linee specificate. Limiti di integrazione in un integrale doppio su una regione delimitata da rette.
prova, aggiunto il 28/03/2014
Linee notevoli del 3° ordine: lista cartesiana, cissoide di Diocle, strofrido, verzier di Agnesi. Linee di quarto e ordine superiore e alcune linee trascendentali: la spirale di Archimede, la curva della discesa più breve. L'area dell'area delimitata dal lemniscate.
tesina, aggiunta il 07/08/2015
Il concetto di integrale definito, il calcolo dell'area, del volume del corpo e della lunghezza dell'arco, del momento statico e del baricentro della curva. Calcolo dell'area nel caso di una regione curvilinea rettangolare. Applicazione di integrali curvilinei, di superficie e tripli.
tesina, aggiunta il 19/05/2011
Derivata di un integrale definito rispetto ad un limite superiore variabile. Calcolo di un integrale definito come limite della somma integrale secondo la formula di Newton-Leibniz, variazione di variabile e integrazione per parti. Lunghezza dell'arco in coordinate polari.
lavoro di controllo, aggiunto il 22/08/2009
Storia del calcolo integrale e differenziale. Applicazioni dell'integrale definito alla soluzione di alcuni problemi di meccanica e fisica. Momenti e centri di massa delle curve piane, teorema di Gulden. Equazioni differenziali. Esempi di problem solving in MatLab.
abstract, aggiunto il 07/09/2009
Integrale curvilineo di prima e seconda specie. L'area dell'area delimitata da una curva chiusa. Il volume di un corpo formato dalla rotazione di una curva chiusa. Centro di massa e momenti di inerzia della curva. Campo magnetico attorno a un conduttore percorso da corrente. L'essenza della legge di Faraday.
Ricorda-quell'oran-stesso-strato-massa-co-ka-ta-fo-te - luce-da-ra-zha-te-se, attaccata-la-u-schi-e-sya ai ferri da maglia ve- lo-si-ped-no-go-ko-le-sa? At-cre-pim ka-ta-fot to sa-mo-mu rim-du ko-le-sa e segui il suo tra-ek-to-ri-she. Secondo le curve lu-chen-nye, sono attaccati alla famiglia del cicloide.
Allo stesso tempo, Ko-le-so è chiamato-zy-va-et-sya about-from-in-dia-circle (o circle-stu) cyclo-lo-and-dy.
Ma dai, torniamo al nostro secolo e ri-sya-dem su un tech-no-ku più moderno. Lungo la strada, ciao, ka-mu-shek è caduto, qualcuno è rimasto bloccato in un pro-tek-to-re ko-le-sa. Pro-ver-now-shi è qualche giro con un co-le-som, dove-yes-le-tit ka-men, quando tradisci dal pro-tek-to-ra? Contro la destra-le-zione del movimento della mo-the-cycle-la o sulla destra-le-tion?
Di fatto, il libero movimento del corpo na-chi-na-et-sya secondo ka-sa-tel-noy a quel tra-ek-that-rii, secondo il quale poi sciamava si muoveva. Ka-sa-tel-naya a cyclo-lo-and-de sempre a destra-le-on-a-destra-le-zione del movimento e passa attraverso il punto superiore ku pro-from-in-dia-circle-no -sti. Nella giusta direzione, il movimento dello stesso-le-tit e del nostro ka-mu-shek.
Ricordi come guidavi nelle pozzanghere durante la tua infanzia su una bicicletta-lo-si-pe-de senza alettone? Mok-para-lo-ka sulla schiena -ta-ta.
Il 17° secolo è il secolo di cyclo-and-dy. I migliori scienziati hanno studiato le sue incredibili proprietà.
Una specie di tra-ek-to-riya porta il corpo, si muove sotto l'azione della forza di gravità, da un punto all'altro per un breve periodo di tè? Questo sarebbe uno dei primi compiti di quel na-at-ki, qualcuno-paradiso che quest'ora non si siede sul nome del numero va-ri-a-tsi-on-noe.
Mi-ni-mi-zi-ro-vat (o mak-si-mi-zi-ro-vat) possono essere cose diverse: la lunghezza del percorso, la velocità, il tempo. Nello za-da-che su bra-hi-cento-crona mi-ni-mi-zi-ru-et-x nome-ma tempo -call-em: greco βράχιστος - il più piccolo, χρόνος - tempo).
La prima cosa che mi viene in mente è un tra-ek-to-riya diretto. Dai, diamo un'occhiata anche al re-re-ver-well-thuyu cyclo-lo-and-du con il punto di ritorno-vra-ta nella parte superiore da for-given-th-check. E, seguendo Ga-li-leo Ga-li-le-em, - four-vert-tin-ku circle-no-sti, collegando-nya-yu-shchy on-shi punti.
Per qualche ragione, Ga-li-leo Ga-li-ley ras-smat-ri-val four-vert-tin-ku circle e ha ritenuto che questo fosse il migliore nel senso le time-me-no tra-ek-that -riya discesa-ka? Ci ha inserito lo-ma-nye e ha notato che con un aumento del numero di collegamenti, il tempo diminuirà. Da-qui-sì, Ga-li-lei è andato naturalmente al cerchio, ma ha tratto la conclusione sbagliata che questa tra-qualcosa -ria è la migliore tra tutte le possibili. Come possiamo vedere, il miglior tra-ek-to-ri-she è-la-et-sya cyclo-lo-and-yes.
Attraverso due punti dati, è possibile passare un unico ciclo-lo-and-du a condizione che nel punto più alto ci sia toch-ka vra-ta tsik-lo-and-dy. E sì, quando il ciclo-lo-and-de viene-ho-dit-sya under-no-mother-sya per passare attraverso il secondo punto, lei sarà ancora Cree -howl nai-sko-rei-she-go discesa !
Un altro one-to-the-beauti-si-vaya for-da-cha, connesso con il cyclo-lo-and-doy, è for-da-cha su ta-at-that-chron. Tradotto dal greco, ταύτίς significa "lo stesso", χρόνος, come già sappiamo - "tempo".
Facciamo tre montagne uno contro uno con pro-fi-lem sotto forma di cyclo-lo-and-dy, in modo che le estremità delle montagne siano gufo-pa-da-li e ras-po-la-ga -lis in cima al ciclo-lo-and-dy. Mettiamo tre bo-ba su diversi te-così-tu e dim-dim from-mash-ku. Udi-vi-tel-ney-shiy fatto - tutti verrebbero giù uno-ora-uomini-ma!
In inverno, puoi costruire una montagna di ghiaccio nel cortile e controllare questa proprietà dal vivo.
For-da-cha su ta-at-that-chrono-st-it in na-ho-de-nii un ululato così storto che, na-chi-naya da any-bo-go-initial- ma allo stesso modo , il tempo per scendere a un dato punto sarà lo stesso.
Hri-sti-en Guy-gens do-ka-zal, che l'unico ta-at-that-chron-noy è-la-et-sya cyclo-lo-and-yes.
Ko-nech-ma, Guy-gen-sa non è una discesa in-te-re-so-val lungo le montagne ghiacciate. A quel tempo, gli scienziati non avevano una tale crescita per-no-mother-for-y-for-mi per amore dell'arte. Per-yes-chi, alcuni-rye ha studiato, era-ho-di-li dalla vita e per-pro-gufi di quei-no-ki di quel tempo-io-no. Nel 17° secolo, co-ver-sha-yut-sya è già lontana piani marittimi. Shi-ro-tu mo-rya-ki puoi determinare-de-lyat già con cento-preciso-ma-accurato-ma, ma sorpresa-vi-tel-ma che non sai come determinare - de-lyat con-tutto. E uno dei pre-la-gav-shih-s-so-bos di-me-re-niya shi-ro-you era os-no-van su na-li-chii accurato chrono-no-met-ditch.
Il primo, che per-du-small del-lat ma-yat-no-no-know-s, qualcuno sarebbe accurato, era Ga-li-leo Ga-li-ley. Tuttavia, in quel momento in cui lui na-chi-na-et li re-a-li-zo-vy-vat, è già vecchio, è cieco e per l'anno rimanente lo scienziato non ha il tempo di fare un guarda nella sua vita. Egli za-ve-shcha-et questo figlio-beh, tuttavia, quella luce di miele e na-chi-na-et for-no-mother-sya may-yat-no-one, la stessa morte e non avendo il tempo di ri-a-li-zo-vat per-ci- siamo seduti. Il prossimo segno dello sciame fu Christi-sti-an Guy-gens.
Ha osservato che re-ri-od-ko-le-ba-niya solitamente-go ma-yat-ni-ka, ras-smat-ri-vav-she-go-sya Ga-li-le-em, per- wee-sit dall'inizio-ma-dello-stesso, cioè da am-pli-tu-dy. Per-pensare a come-va dovrebbe essere un tra-ek-that-riya del movimento di un carico, in modo che il tempo di ka-che-tion su di esso non sia -se-lo da am-pli-tu -dy, ha re-sha-et for-da-chu su ta-at-that-chron. Ma come spostare il carico lungo il ciclo-lo-and-de? Pe-re-vo-dya theo-re-ti-che-research-before-va-tion nel pratico-ti-che-plane, Guy-gens de-la-et "cheeks", su qualcuno-segale na- ma-you-va-et-sya ve-roar-ka ma-yat-no-ka, e re-sha-et qualche altro compito ma-te-ma-ti-che. Fa-ka-zy-va-et che le "guance" dovrebbero avere il profilo dello stesso ciclo-lo-and-dy, allo stesso modo in cui evo-lu-that cycle-lo-and-dy yav-la- et-sya cycle-lo-and-yes con lo stesso pa-ra-met-ra-mi.
In aggiunta a ciò, la costruzione pre-lo-femmina di Guy-gen-som del cyclo-lo-and-far-no-go ma-yat-no-ka pone-in-la-et by -count la lunghezza di il ciclo-lo-and-dy. Se c'è un blue-no-dot-ku, la lunghezza-per-qualche-sciame è uguale a quattro-you-rem ra-di-u-sam about-from-in-dya-sche-go circle, mak- si-mal-ma da-clo-thread, allora la sua fine sarà al punto di re-re-se-che-niya "guance" e cyclo-lo-and-dy-tra- ek-to-rii, cioè in cima al cyclo-lo-and-dy- “cheek-ki”. Poiché questo è in-lo-vi-sulla lunghezza di ar-ki cyclo-and-dy, allora la lunghezza totale è uguale a otto ra-di-u-sam pro-of-in-uncle-th circle.
Christ-sti-an Guy-gens ha fatto un ma-yat-nik ciclico-lo-e-distante, e ore con lui pro-ho-di-se-py-ta-niya nel mare pu-te-she- stvi-yah, ma non è venuto. Tuttavia, proprio come gli orologi con il solito maya-nessuno per questi scopi.
Da-cosa, uno a uno, ancora su-sche-stu-yut cha-so-me-ha-bottom-noi con il solito-ma-vein-ny maya-nessuno? Se lo guardi, allora con piccoli from-clo-not-no-yah, come il red-no-go may-yat-no-ka, "guance" cyclo-lo- e-far-but-go ma- yat-no-ka quasi nessuna influenza eye-zy-va-yut. Di conseguenza, il movimento lungo il ciclico-lo-and-de e attorno alla circonferenza con un piccolo from-clo-no-no-yah è quasi gufo-pa-sì-yut.
5. Equazione parametrica della cicloide e equazione in coordinate cartesiane
Supponiamo di avere una cicloide formata da una circonferenza di raggio a centrata nel punto A.
Se scegliamo come parametro che determina la posizione del punto, l'angolo t=∟NDM, di cui è riuscito a girare il raggio, che aveva una posizione verticale AO all'inizio della laminazione, allora le coordinate xey del punto M sarà espresso come segue:
x \u003d OF \u003d ON - NF \u003d NM - MG \u003d at-a sin t,
y= FM = NG = ND - GD = a - un cos t
Quindi le equazioni parametriche della cicloide hanno la forma:

Quando si cambia t da -∞ a +∞, si ottiene una curva costituita da un insieme innumerevole di tali rami, che è mostrata in questa figura.
Inoltre, oltre all'equazione parametrica della cicloide, c'è anche la sua equazione in coordinate cartesiane:
Dove r è il raggio del cerchio che forma la cicloide.
6. Problemi per trovare parti di una cicloide e figure formate da una cicloide
Compito numero 1. Trova l'area di una figura delimitata da un arco di una cicloide la cui equazione è data parametricamente
![]()
e asse Oh.

Soluzione. Per risolvere questo problema, utilizziamo i fatti a noi noti dalla teoria degli integrali, vale a dire:
L'area del settore curvilineo.
Si consideri una funzione r = r(ϕ) definita su [α, β].
ϕ 0 ∈ [α, β] corrisponde a r 0 = r(ϕ 0) e, quindi, il punto M 0 (ϕ 0 , r 0), dove ϕ 0 ,
r 0 - coordinate polari del punto. Se ϕ cambia, “percorrendo” l'intero [α, β], allora il punto variabile M descriverà una certa curva AB data da
l'equazione r = r(ϕ).
Definizione 7.4. Un settore curvilineo è una figura delimitata da due raggi ϕ = α, ϕ = β e una curva AB data in polare
coordinate dall'equazione r = r(ϕ), α ≤ ϕ ≤ β.
Il seguente
Teorema. Se la funzione r(ϕ) > 0 ed è continua su [α, β], allora l'area
il settore curvo è calcolato con la formula:

Questo teorema è stato dimostrato in precedenza nell'argomento di un integrale definito.
Sulla base del teorema di cui sopra, il nostro problema di trovare l'area di una figura delimitata da un arco della cicloide, la cui equazione è data dal parametrico x= a (t - sin t) , y= a ( 1-cos t) e l'asse Ox, è ridotto alla soluzione seguente.
Soluzione. Dall'equazione della curva dx = a(1−cos t) dt. Il primo arco della cicloide corrisponde alla variazione del parametro t da 0 a 2π. Di conseguenza,

Compito numero 2. Trova la lunghezza di un arco della cicloide
![]()
Il seguente teorema e il suo corollario sono stati studiati anche nel calcolo integrale.
Teorema. Se la curva AB è data dall'equazione y = f(x), dove f(x) e f ' (x) sono continui su , allora AB è rettificabile e
Conseguenza. Sia AB dato parametricamente
LAB = ![]() (1)
(1)
Siano le funzioni x(t), y(t) continuamente differenziabili su [α, β]. Quindi
la formula (1) può essere scritta come

Facciamo un cambio di variabili in questo integrale x = x(t), quindi y'(x)= ;
dx= x'(t)dt e quindi:

Ora torniamo a risolvere il nostro problema.
Soluzione. Abbiamo e quindi
Compito numero 3. È necessario trovare la superficie S formata dalla rotazione di un arco della cicloide
L=((x,y): x=a(t - sin t), y=a(1 - costo), 0≤ t ≤ 2π)
Nel calcolo integrale, esiste la seguente formula per trovare l'area della superficie di un corpo di rivoluzione attorno all'asse x di una curva definita parametricamente su un segmento: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)
Applicando questa formula alla nostra equazione cicloide, otteniamo:

Compito numero 4. Trova il volume del corpo ottenuto ruotando l'arco della cicloide
![]()
Lungo l'asse Ox.
Nel calcolo integrale, quando si studiano i volumi, c'è la seguente osservazione:
Se la curva che delimita il trapezio curvilineo è data da equazioni parametriche e le funzioni in queste equazioni soddisfano le condizioni del teorema sul cambiamento di variabile in un certo integrale, allora il volume del corpo di rotazione del trapezio attorno all'asse Ox sarà essere calcolato con la formula

Usiamo questa formula per trovare il volume di cui abbiamo bisogno.
Problema risolto.
Conclusione
Quindi, nel corso di questo lavoro, sono state chiarite le principali proprietà della cicloide. Hanno anche imparato a costruire una cicloide, hanno scoperto il significato geometrico della cicloide. Come si è scoperto, la cicloide ha un'enorme applicazione pratica non solo in matematica, ma anche nei calcoli tecnologici, in fisica. Ma la cicloide ha altri pregi. Fu usato dagli scienziati del 17° secolo nello sviluppo di metodi per lo studio delle linee curve, quei metodi che alla fine portarono all'invenzione del calcolo differenziale e integrale. Fu anche una delle "pietre di paragone" su cui Newton, Leibniz ei loro primi ricercatori testarono il potere di nuovi e potenti metodi matematici. Infine, il problema del brachistocrono ha portato all'invenzione del calcolo delle variazioni, tanto necessario per i fisici di oggi. Pertanto, la cicloide era indissolubilmente legata a uno dei periodi più interessanti della storia della matematica.
Letteratura
1. Berman G.N. Cicloide. - M., 1980
2. Verov SG Brachistocrono, o un altro segreto del cicloide // Kvant. - 1975. - N. 5
3. Verov SG Segreti del cicloide// Kvant. - 1975. - N. 8.
4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Applicazioni di un integrale definito. Linee guida e compiti individuali per gli studenti del I anno della Facoltà di Fisica. - Rostov n / a: UPL RSU, 1994.
5. Gindikin SG L'età delle stelle di un cicloide // Kvant. - 1985. - N. 6.
6. Fikhtengolts G.M. Corso di calcolo differenziale e integrale. T.1. - M., 1969
Tale linea è chiamata "busta". Ogni linea curva è l'involucro delle sue tangenti.
Materia e movimento, e il metodo che costituiscono, consentono a tutti di realizzare il proprio potenziale nella conoscenza della verità. Lo sviluppo di una metodologia per lo sviluppo di una forma di pensiero dialettica-materialistica e la padronanza di un simile metodo cognitivo è il secondo passo verso la soluzione del problema dello sviluppo e la realizzazione delle possibilità dell'Uomo. Frammento XX Opportunità...
La situazione può ammalarsi di nevrastenia - nevrosi, la cui base del quadro clinico è una condizione astenica. Sia nel caso della nevrastenia che nel caso dello scompenso della psicopatia nevrastenica, l'essenza della protezione spirituale (psicologica) si manifesta con un allontanamento dalle difficoltà verso una debolezza irritabile con disfunzioni vegetative: o una persona inconsciamente "combatte" più da un attacco ...





Vari tipi di attività; sviluppo dell'immaginazione spaziale e delle rappresentazioni spaziali, del pensiero figurativo, spaziale, logico, astratto degli scolari; la formazione di abilità per applicare conoscenze e abilità geometriche e grafiche per risolvere vari problemi applicati; familiarizzazione con il contenuto e la sequenza delle fasi delle attività del progetto nel campo tecnico e ...
Archi. Le spirali sono anche evolventi di curve chiuse, come l'evolvente di un cerchio. I nomi di alcune spirali sono dati dalla somiglianza delle loro equazioni polari con le equazioni delle curve in coordinate cartesiane, ad esempio: spirale parabolica (a - r)2 = bj, spirale iperbolica: r = a/j. Asta: r2 = a/j si-ci-spirale, le cui equazioni parametriche assomigliano a: , )