Мэдлэгийн санд сайн ажлаа илгээх нь энгийн зүйл юм. Доорх маягтыг ашиглана уу
Мэдлэгийн баазыг суралцаж, ажилдаа ашигладаг оюутнууд, аспирантууд, залуу эрдэмтэд танд маш их талархах болно.
Нийтэлсэн http://www.allbest.ru/
боловсролын байгууллага
"Беларусийн улсын сурган хүмүүжүүлэх сургууль
Максим танкийн их сургууль
Физик-математикийн факультет
Математик, Математик заах арга зүйн тэнхим
СЭДЭВТ ДЭЭРХ СУРГАЛТЫН АЖИЛ
"ЦИКЛОИД"
Минск, 2016 он
cycloid arch tautochronous дүүжин
- Оршил
- 1. Циклоидын үндсэн шинж чанарууд
- 2. Циклоид геометрийн тодорхойлолт
- 3. Циклоид нуман хаалганы талбай
- 4. Циклоид нумын нумын урт
- 5. Циклоид нумыг эргүүлэх замаар олж авсан биеийн эзэлхүүн
- 6. Хамгийн сайн дүүжин
- Дүгнэлт
- Ном зүй
ОРШИЛ
Миний курсын ажлын сэдэв бол циклоид юм. Энэ муруй нь олон талаараа гайхалтай юм. Энэ нь мөн эргэлдэж буй дугуйны ирмэгийн цэгийн ул мөр, энэ нь мөн тогтмол хугацааны хэлбэлзлийн муруй, мөн хамгийн хурдан буух муруй юм. Өнөө үед циклоидын муруйг техникийн олон тооцоололд ашигладаг бөгөөд эдгээр муруйнуудын талаархи мэдлэг нь машины эд ангиудыг судлахад хялбар болгодог. Нарийвчилсан мэдээлэлгүйгээр бид циклоид муруйны шинж чанарыг араа шүдний профиль барих болон бусад олон техникийн асуудалд ашигладаг болохыг дурдъя. Цэвэр хэрэглээний үүднээс ч гэсэн эдгээр муруйнууд нь хамгийн нухацтай анхаарал хандуулах ёстой. Тиймээс би энэ сэдвийг судлахад хамааралтай, сонирхолтой гэж үзсэн.
Циклоид судлахад ямар асуудал гардаг вэ? Юуны өмнө механикаас хамааралгүй цэвэр геометрийн тодорхойлолтыг өгөх шаардлагатай. Дараа нь та түүний шинж чанарыг судалж, шүргэгчийг анхаарч үзэх хэрэгтэй, циклоидын нуман ба түүний суурьтай хязгаарлагдах талбай, нумын урт, циклоидын нуман хаалганы эргэн тойронд эргүүлэх замаар үүссэн биеийн эзэлхүүнийг тооцоолох хэрэгтэй. хөтөч шугам.
Курсын ажил нь циклоидын tautochronous шинж чанар, түүний хамгийн сайн дүүжин үүсгэх хэрэглээг нарийвчлан авч үзэх болно. Савлууртай цагны ач холбогдлыг дутуу үнэлж болохгүй, учир нь тэд саяхан болтол одон орны ажиглалтын газруудад цаг хугацааны үйлчилгээг баталгаажуулсан хамгийн нарийвчлалтай цаг болж байсан.
Циклоидуудын бас нэг ач тусыг тэмдэглэх нь зүйтэй бөгөөд үүнийг эрдэмтэд муруй шугамыг судлах арга техникийг боловсруулахад ашигласан нь дифференциал ба интеграл тооцоог зохион бүтээхэд хүргэсэн явдал юм. Би ажилдаа циклоид нумын нумын урт, нуман доорх гадаргуугийн талбай, интеграл тооцоолол үүсэхээс өмнө циклоид нумын эргэлтээс үүссэн биеийн эзэлхүүний тооцоог харьцуулахыг санал болгож байна. Үргэлж туйлын хатуу бөгөөд интеграцчлалыг ашигладаг.
Зорилго:"Циклоид" сэдвээр материалыг судлах; хамгийн сайн дүүжингийн шинж чанарыг судлах; интеграл тооцоо гарч ирэхээс өмнөх ба дараа муруй шугамын судалгааны харьцуулалт, циклоид нумын нумын урт, нуман доорх гадаргуугийн талбай, циклоид нумын эргэлтээс үүссэн биеийн эзэлхүүнийг тооцоолох.
1. ЦИКЛОДИГИЙН ҮНДСЭН ШИНЖ
Эхлээд та ямар төрлийн муруйг циклоид гэж нэрлэдэгийг олж мэдэх хэрэгтэй.
Радиустай тойргийг авч үзье а A цэг дээр төвлөрсөн. Тухайн тойрог OX тэнхлэгийн дагуу гулсахгүй эргэлдэнэ. Тойргийн аль ч цэгээр дүрслэгдсэн муруйг дуудна циклоид.
Циклоид хэмээх энэхүү тодорхойлолт нь эрдэмтдийн сэтгэлд нийцээгүй: эцэст нь энэ нь механик ойлголтууд дээр суурилдаг - хурд, хөдөлгөөний нэмэгдэл гэх мэт. Тиймээс геометрүүд циклоидод "цэвэр геометрийн тодорхойлолт" өгөхийг үргэлж эрэлхийлсээр ирсэн. Ийм тодорхойлолтыг та эхлээд механик тодорхойлолтыг ашиглан циклоидын үндсэн шинж чанарыг судлах хэрэгтэй. Эдгээр шинж чанаруудаас хамгийн энгийн бөгөөд хамгийн онцлог шинж чанарыг сонгосноор бид үүнийг геометрийн тодорхойлолтын үндэс болгон ашиглаж болно.
Циклоидтай шүргэгч ба нормальыг судалж эхэлцгээе. Юу шүргэгчмуруй шугам руу, хүн бүр хангалттай тодорхой төсөөлдөг; Тиймээс бид энд танилцуулахгүй. хэвийншүргэгч рүү перпендикуляр гэж нэрлэгддэг, контактын цэг дээр сэргээгдсэн. Зураг дээр. 1.1-д M цэг дээрх AB муруйн шүргэгч ба нормальыг харуулав.
Циклоидыг авч үзье (Зураг 1.2). Тойрог AB шулуун шугамаар эргэлддэг. Эхний мөчид циклоидын хамгийн доод цэгийг дайран өнгөрч байсан тойргийн босоо радиус нь χ өнцгөөр эргэлдэж, OM байрлалыг эзэлсэн гэж үзье. Өөрөөр хэлбэл, M o T сегмент нь M o M 1 сегментийн тийм хэсэг бөгөөд q өнцөг нь бүтэн эргэлтээс байна гэж бид үзэж байна. Энэ тохиолдолд М 0 цэг нь М цэгт хүрэв.
М цэг нь бидний сонирхдог циклоидын цэг юм.
Сум Өөөнхрөх тойргийн төвийн хурдыг илэрхийлнэ. Тойргийн бүх цэгүүд, түүний дотор М цэг нь ижил хэвтээ хурдтай байдаг.Гэхдээ М цэг нь тойргийн эргэлтэнд оролцдог. Энэ эргэлтийн үед тойрог дээрх М цэгийн хүлээн авах хурд MC нь тангенциалаар чиглэнэ MS 1 тойрог руу, өөрөөр хэлбэл радиустай перпендикуляр ОМ.Тэгээд тэрнээс хойш Энэ тохиолдолд MS хурд нь MP хурдтай тэнцүү байна (жишээ нь, хурд HE).Тиймээс бидний хөдөлгөөний үед хурдны параллелограмм нь ромб байх болно (Зураг 1.2-т MSKR-ийн ромбус). Энэ ромбын MK диагональ нь циклоид руу шүргэгчийг өгөх болно.
Дээр дурдсан бүх зүйл нь дараахь барилгын асуудлыг шийдвэрлэх боломжтой болгодог: циклоидын чиглүүлэгч шугам AB, үүсгэгч тойргийн r радиус, циклоидод хамаарах M цэг (Зураг 1.2). Циклоид руу MK-ийн шүргэгчийг барих шаардлагатай.
М цэгтэй бол бид тойрог дээрх цэг M цэгт унах үед үүсгэгч тойргийг хялбархан барьж чадна. Үүнийг хийхийн тулд бид эхлээд төвийг олно. Орадиус ашиглан MO= r (О цэг нь AB-тай параллель шулуун дээр, түүнээс r зайд байх ёстой). Дараа нь бид чиглүүлэгч шугамтай параллель дурын урттай MP сегментийг байгуулна. Дараа нь бид шугам барина MS 1 , перпендикуляр ОМ. Энэ мөрөнд бид цэгээс чөлөөлөгдсөн Мсегмент MC нь MP-тэй тэнцүү. Хажуугийн нэгэн адил MS ба MP дээр бид ромбус барьдаг. Энэ ромбын диагональ нь M цэг дээрх циклоидтой шүргэгч байх болно.
Энэхүү барилга нь зөвхөн геометрийн шинж чанартай боловч бид үүнийг механикийн үзэл баримтлалыг ашиглан олж авсан. Одоо бид механикчдад баяртай гэж хэлж, түүний тусламжгүйгээр цаашдын үр дагаврыг авч чадна. Энгийн теоремоор эхэлцгээе.
Теорем 1. Циклоид шүргэгч хоорондын өнцөг (дурын цэг дээр)ба чиглүүлэх шугам нь нөхөхтэй тэнцүү байна 90°үүсгэгч тойргийн радиусын эргэлтийн өнцгийн хагас.
Өөрөөр хэлбэл, Зураг дээр. 1.2
? KLTтэнцүү буюу
Одоо бид энэ тэгш байдлыг батлах болно. Яриа богиносгохын тулд бид үүсгэгч тойргийн радиусын эргэлтийн φ өнцгийг "үндсэн өнцөг" гэж нэрлэхийг зөвшөөрнө. Энэ нь Зураг дээрх MOT өнцөг гэсэн үг юм. 1.2 - үндсэн өнцөг. Гол өнцөг нь хурц байна гэж бид таамаглах болно. Өнхрөх тойрог бүтэн эргэлтийн дөрөвний нэгээс илүү байх тохиолдолд нотлох баримт нь ижил байх болно.
CMP өнцгийг анхаарч үзээрэй. CM тал нь перпендикуляр байна ОМ(тойрогтой шүргэгч нь радиустай перпендикуляр байна). Хажуугийн MP (хэвтээ) перпендикуляр FROM(босоо чиглэлд). Гэхдээ нөхцөл байдлаас харахад MOP өнцөг нь хурц, CMP өнцөг нь мохоо байна. Тиймээс булангууд ОУХБболон SMR 180 ° хүртэл нэмнэ (харилцан перпендикуляр талуудтай өнцөг, тэдгээрийн нэг нь хурц, нөгөө нь мохоо).
Тиймээс CMP өнцөг нь 180 ° -ts-тэй тэнцүү байна. Гэхдээ та мэдэж байгаагаар ромбын диагональ нь орой дээрх өнцгийг хоёр хуваадаг. Тиймээс, Хюго
KMR = 90° -,
Q.E.D.
Одоо циклоидын ердийн зүйлд анхаарлаа хандуулцгаая. Зургийн зүүн талыг дүрсэлцгээе. 1.2 нь илүү том, хэвийн зурж үзье БИ (БИ ? MK; будаа. 1.3).
Зураг дээрээс. 1.3-аас харахад EMP өнцөг нь өнцгийн зөрүүтэй тэнцүү байна KMEболон KMR, өөрөөр хэлбэл 90°-тай тэнцүү - ? KMP.
Гэхдээ бид зүгээр л булан өөрөө гэдгийг нотолсон KMR 90°-тай тэнцүү -
Тиймээс бид дараахь зүйлийг авна.
? RME= 90° -? KMR= 90° - (90° -) =
Бид энгийн боловч хэрэгтэй теоремыг баталсан. Үүнийг томъёолъё:
Теорем 2.Нормалаас циклоидын хоорондох өнцөг (түүний аль ч үед)ба чиглүүлэгч шугам нь "үндсэн өнцөг" -ийн хагастай тэнцүү байна.
Одоо үүсгэгч тойргийн "цэгийг (T) M цэгтэй" (циклоидын "одоогийн" цэг) "доод" (үүсгүүрийн тойрог ба чиглүүлэх шугамтай) холбоно. Зураг 1.3). Гурвалжин MOT нь ижил өнцөгт (OM ба FROMүүсгэгч тойргийн радиусууд). Энэ гурвалжны суурь дахь өнцгүүдийн нийлбэр нь 180 ° - u-тэй тэнцүү бөгөөд суурийн өнцөг бүр нь энэ нийлбэрийн хивс юм. Тэгэхээр, ? OMT = 90° -.
Буланд анхаарлаа хандуулаарай RMT.Энэ нь өнцгийн зөрүүтэй тэнцүү байна HTAболон OMR. Одоо бид үүнийг харсан ? OMT 90 ° -тай тэнцүү; OMP өнцгийн хувьд энэ нь юутай тэнцүү болохыг олоход хэцүү биш юм. Эцсийн эцэст, булан OMRөнцөгтэй тэнцүү байна DOM(зэрэгцээ байх үед дотоод хөндлөн хэвтэх өнцөг).
Энэ нь шууд тодорхой харагдаж байна ? DOM 90 ° - c-тэй тэнцүү. гэсэн үг, ? OMP= = 90° - c. Тиймээс бид дараахь зүйлийг авна.
RMT = ? HTA - ? OMR \u003d 90 ° - - (90 ° - c) \u003d.
Энэ нь гайхалтай үр дүнд хүрч байна: өнцөг RMT PME өнцөгтэй тэнцүү байна (теорем 2). Тиймээс шууд ME болон MT хоёр нэгдэх болно! Манай будаа. 1.3 нь тийм ч зөв хийгдээгүй байна! Шугамын зөв зохицуулалтыг зурагт үзүүлэв. 1.4.
Олж авсан үр дүнг теорем 3 хэлбэрээр томъёолъё.
Теорем 3 (циклоидын анхны үндсэн шинж чанар).Циклоидын хэвийн хэмжээ нь үүсгэгч тойргийн "доод" цэгээр дамждаг.
Энэ теорем нь энгийн үр дагавартай. Шүргэгч ба нормаль хоёрын хоорондох өнцөг нь тодорхойлолтоор бол зөв өнцөг юм. Энэ нь үүсгэгч тойргийн тойрогт бичигдсэн өнцөг юм. Тиймээс энэ нь тойргийн голч дээр үндэслэсэн байх ёстой. Тэгэхээр, ТТ 1 -- диаметр ба T 1 -- үүсгэгч тойргийн "дээд" цэг. Хүлээн авсан үр дүнг томъёолъё.
Үр дагавар (циклоидын хоёр дахь үндсэн шинж чанар).Циклоид руу шүргэгч нь үүсгэгч тойргийн "дээд" цэгээр дамждаг.
Энэ шинж чанарыг тайлбарлахын тулд бид циклоидыг бүтээх хэрэгтэй.
Циклоид барих ажлыг дараах дарааллаар гүйцэтгэнэ.
1. Чиглүүлэгч хэвтээ шугам дээр r радиус үүсгэгч тойргийн урттай тэнцүү AA 12 сегментийг тавьсан, (2pr);
2. r радиустай үүсгэгч тойргийг байгуулж, чиглүүлэх шугам нь А цэгт шүргэнэ;
3. AA 12 тойрог ба сегмент нь хэд хэдэн тэнцүү хэсгүүдэд хуваагдана, жишээ нь 12;
4. 1 1 , 2 1 , ...12 1 хуваах цэгүүдээс тойргийн хэвтээ тэнхлэгийг 0 1 , 0 2 , ... 0 12 цэгт үргэлжлүүлж огтлолцох перпендикуляруудыг сэргээнэ;
5. 1, 2, ... 12-р тойргийн хуваах цэгүүдээс хэвтээ шулуун шугамуудыг зурж, тэдгээр дээр r радиустай тойргийн нумуудтай серифүүдийг хийсэн;
6. Авсан A 1 , A 2 , ... A 12 цэгүүд нь циклоидод хамаарна.
Зураг дээр. 1.6 циклоидын суурь нь 6 тэнцүү хэсэгт хуваагдана;
Хэсэгчилсэн тоо их байх тусам зураг илүү нарийвчлалтай байх болно. Бидний бүтээсэн циклоидын цэг бүр дээр муруйн цэгийг үүсгэгч тойргийн "дээд" цэгтэй холбосон шүргэгч зурдаг. Бидний зурган дээр бид долоон шүргэгч (тэдгээрийн хоёр нь босоо) авсан. Одоо циклоидыг гараар зурахдаа бид эдгээр шүргэгч тус бүрт үнэхээр хүрч байгаа эсэхийг анхаарч үзэх болно: энэ нь зургийн нарийвчлалыг мэдэгдэхүйц нэмэгдүүлэх болно. Энэ тохиолдолд циклоид өөрөө эдгээр бүх шүргэгчийг тойрон гарах болно).
Үүнтэй ижил инжир дээр хийцгээе. Циклоид олдсон бүх цэгүүдэд 1.6 хэвийн байна. Хөтөчийг тооцохгүй нийтдээ таван хэвийн байх болно. Эдгээр нормуудын дугтуйг өөрийн гараар бүтээх боломжтой. Хэрэв бид зургаагийн оронд 12 эсвэл 16 хуваах цэгийг авсан бол зурган дээр илүү олон хэвийн зүйл гарч ирэх бөгөөд дугтуйг илүү тодорхой дүрслэх болно. Бүх нормуудын ийм дугтуй нь аливаа муруй шугамын шинж чанарыг судлахад чухал үүрэг гүйцэтгэдэг. Циклоидын хувьд нэгэн сонин баримт илчлэв: циклоидын хэвийн дугтуй нь яг ижил циклоид бөгөөд зөвхөн 2-оор шилждэг. адоош болон дээр рабаруун талд. Энэ баримт нь циклоидын онцлог шинж юм.
2. ЦИКЛОДИГИЙН ГЕОМЕТРИЙН ТОДОРХОЙЛОЛТ
Одоо бид циклоидыг механик ашиглахгүйгээр цэгүүдийн байрлал гэж тодорхойлж байна. Үүнийг хийх нь хамгийн хялбар юм. Дурын шугамыг авч үзье AB(бид нөхцөлт байдлаар түүний чиглэлийг хэвтээ гэж үзэх болно) ба түүн дээрх цэг М 0 . Дараа нь энэ шугамтай шүргэгч, түүний нэг талд байрлах тодорхой радиусын бүх боломжит тойргийг авч үзье. Цэгээс тойрог бүр дээр Тшулуун шугамаар шүргэх ABхойш тавих (цэгний чиглэлд М 0 ) нуман tm,сегменттэй тэнцүү урттай М 0 Т.Цэгүүдийн байршил М(бидний дурдсан бүх тойрог дээр авсан) ба циклоид байх болно.
Циклоид өөр нэг чухал шинж чанарыг тогтоож, энэ муруйг судлах үндэс болгон ашиглахыг хичээцгээе.
Гурвалжинг авч үзье MTT 1 (Зураг 2.1), үүсгэгч тойргийн босоо диаметр, циклоидын шүргэгч ба түүний хэвийн хэмжээнээс үүссэн.
Булан MT 1 Т, тойрог дотор бичээстэй адил нуман дээр тулгуурласан төв өнцгийн хагастай тэнцүү, өөрөөр хэлбэл тэнцүү байна. зарцуулцгаая MK||AB болон БИ?AB. ME сегмент нь ирээдүйд чухал үүрэг гүйцэтгэх тул бид түүнд нэр, тэмдэглэгээ өгөх болно: бид үүнийг циклоидын М цэгийн "өндөр" гэж нэрлээд үсгээр тэмдэглэнэ. h.Тиймээс цэгийн өндөр Мциклоидууд нь чиглүүлэх шугамаас түүний зай юм.
KMT өнцөгт анхаарлаа хандуулцгаая. Энэ нь өнцөгтэй тэнцүү байна MT 1 Т. Гурвалжингаас TMT 1 бид авах:
MT = 2 анүгэлмөн TKM гурвалжингаас:
CT = MT нүгэл.
Эдгээр үр дүнг харьцуулж, CT = h байгааг анзаарснаар бид эцэст нь дараахь зүйлийг олж авна.
h = 2 анүгэл 2.
Бид M цэгийн өндрийг M цэг дээрх шүргэгч ба босоо тэнхлэгийн хоорондох өнцгөөр илэрхийлсэн (бид AB шулуун шугамын чиглэлийг хэвтээ гэж үздэг хэвээр байна). Одоо энэ өнцгийн синусыг "өндөр"-ээр илэрхийлье. Бид мэдээжийн хэрэг:
хаашаа дамжина көгөгдсөн циклоидын утгын тогтмолыг тэмдэглэв . Бид олж авсан үр дүнг теоремоор илэрхийлнэ.
Теорем 4.М цэг дэх циклоид руу шүргэгч ба босоо тэнхлэгийн хоорондох өнцгийн синус нь М цэгийн "өндөр"-ийн квадрат язгууртай пропорциональ байна.
Аливаа циклоид энэ шинж чанарыг эзэмшдэг нь ойлгомжтой. Асуулт гарч ирнэ: энэ шинж чанар нь циклоидыг яг ямар хэмжээгээр тодорхойлдог вэ: энэ шинж чанарыг агуулсан муруй заавал циклоид байх уу? Энэ нь ийм байх болно, -- дараах (урвуу) теорем бас үнэн болохыг баталж болно.
Теорем 5. AB шугам ба M цэгийг өгвөл теорем 4-ийн нөхцлийг хангаж, M цэгийг дайран өнгөрөх цорын ганц муруй нь циклоид болно.
Түүнээс гадна энэ циклоидын үүсгэгч тойргийн радиус нь коэффициенттэй холбоотой байдаг к, 4-р теоремд дурдсаныг дараах хамаарлаар илэрхийлнэ:.
Өөр нэг гайхалтай муруйг анхаарч үзэх нь зүйтэй циклоидын хамтрагч.
Циклоидыг авч үзье (Зураг 2.2). Түүний M цэгээс бид үүсгэгч тойргийн босоо диаметртэй перпендикулярыг буулгана. P цэгийг авцгаая. Энэ барилгыг циклоидын бүх цэгүүдэд үл хамаарахгүйгээр хийцгээе.
Дараа нь P цэг нь зарим муруйг дүрслэх болно. Энэ муруйг циклоидын хамтрагч гэж нэрлэдэг.
Циклоид, түүн дээрх M цэг ба хиймэл дагуулын харгалзах P цэгийг авч үзье (Зураг 2.3) үүсгэгч тойргийн төвийг үсгээр тэмдэглэнэ. Q. Дараа нь бидэнд:
QP=ЧМ cos?MQP= а cos(180 0 -ts)=- а cosц=- а sin(90 0 -ts)= анүгэл (c -90 0).
Бид үүсгэгч тойргийн төвүүдийн байршлыг зурцгаая (шулуун шугам XX 1 ). цэгээс М 0 хойш тавих ABшугамын сегмент М 0 К, тэнцүү. зарцуулцгаая KY ? XX 1 . Эдгээр шугамын огтлолцох цэгийг үсгээр тэмдэглэнэ О. Шугамын сегмент М 0 Рциклоидын үзүүрээс үүсгэгч тойргийн хүрэлцэх цэг хүртэл чиглүүлэх шулуун шугам дээр тэнцүү байна. а c, энд c нь үндсэн өнцөг MQР, радианаар илэрхийлнэ. Шугамын сегмент OQхэвтээ тэнхлэгт XX 1 тэнцүү байна М 0 Р - М 0 К=а(c -) ба сегмент QPтэнцүү байна анүгэл үү? PMQ, i.e. өнцгийн синустай тэнцүү (c -), радиусаар үржүүлсэн а.
Тиймээс цэгээс Охэвтээ байдлаар тойргийн нумуудтай тэнцүү урттай сегментүүдийг зурж, эдгээр нумануудад тохирох өнцгийн синусуудын босоо шугамын дагуу зурна. Энэ бол бидний мэддэг ердийн синусоидын бүтээн байгуулалт юм.
гэсэн үг, Циклоидын хамтрагчийг синусоид гэж нэрлэдэг.
Бид энэ үнэхээр гайхалтай муруйн шинж чанарыг судлахгүй, зөвхөн баримт болгон тэмдэглэх болно. Циклоид ба түүний суурийн нэг нуман хаалганы хамт хүрээлэгдсэн талбай нь үүсгэгч тойргийн талбайгаас хоёр дахин их байна.
3. ЦИКЛОДИ НУМЫН ТАЛБАЙ
Циклоид нуман хаалга ба түүний суурийн хоорондох талбайн тооцооны тухай анхны дурдагдсан зүйл нь Вивиани, Торричелли нарын бүтээлүүдэд байдаг. Үүний зэрэгцээ тэд "хуваагдах боломжгүй арга" гэж нэрлэгддэг тусгай арга техникийг ашигласан. Энэ арга нь муруй шугаман дүрсийг хязгааргүй нимгэн тууз болгон хувааж, талбайг нь олоход харьцангуй хялбар бөгөөд дараа нь эдгээр хэсгүүдийг нэмж оруулдаг. Энэхүү техник нь хагас зуун жилийн дараа интеграл тооцоолол гарч ирэхэд хүргэсэн.
Циклоид нуман болон синусоидоор хязгаарлагдсан дүрсийг авч үзье. Зураг 3.1-д хоёр дэлбээнээс бүрдсэн энэ дүрсийг бүдүүн зураасаар дугуйлсан байна. Түүний талбайг тооцоолъё.
Юуны өмнө AB чиглүүлэгч шулуун шугамтай харьцуулахад дүрсийн баруун дэлбээний толин тусгал дүрсийг бүтээцгээе (энэ тусгалыг 4.1-р зурагт тасархай шугамаар үзүүлэв). Дараа нь энэ тасархай муруйг зүүн тийш дээш хөдөлгөж, дэлбээ бүрийн контурт багтсан синусоидуудын нумууд давхцахын тулд зүүн дэлбээнд наа. Бид 3.1-р зурагт сүүдэрлэж, Зураг дээр тусад нь дүрсэлсэн гүдгэр дүрсийг авдаг. 3.2. Энэ дүрсийг нэрлэдэг Робервалын дүр. Энэ зургийн хамгийн чухал шинж чанарыг тогтооцгооё.
1. М 0 RLM гүдгэр дүрс нь 3.1-р зурагт бүдүүн зураасаар дүрсэлсэн хоёр дэлбээтэй дүрстэй тэнцүү хэмжээтэй байна. Энэ нь ижил дэлбээтэй "бүрдсэн" байдлаас харагдаж байна.
2. Гүдгэр дүрсийн аливаа хэвтээ хөвч нь АВ-аас ижил зайд байгаа дэлбээний хөвчний хоёр дахин ихтэй тэнцүү байна. Үнэн хэрэгтээ, үүсгэгч тойргоос ижил зайд байрлах баруун дэлбээний CE ба PH хөвч (Зураг 3.1) нь төвөөс ижил зайд байрладаг. Тиймээс CT \u003d CE \u003d PH \u003d P 1 H 1 \u003d TL.
Энэ нь чухал үр дүнг өгдөг: гүдгэр дүрсийн хөвч MR (Зураг 3.2) нь чиглүүлэх шугамаас ижил зайд байрлах SK үүсгэгч тойргийн хөвчтэй тэнцүү байна.
Одоо Робервалын гүдгэр дүрс ба ижил AB ба A 1 B 1 шулуунтай шүргэгч тойргийг авч үзээд тэдгээрийн огтлолцлын цэгүүдийг тойрог ба гүдгэр дүрсийн контуртай дараалан шулуун шугамын хэрчмүүдээр холбоно. зурагт үзүүлэв. Ийнхүү олж авсан бичээстэй олон өнцөгтүүдийг (HLMNPQRSTK ба H 1 L 1 M 1 N 1 P 1 Q 1 R 1 S 1 T 1 K 1) хэд хэдэн трапецын (болон гурвалжин) "харгалзах" олон өнцөгт гэж нэрлэнэ. Тойрог болон Робервелийн зураг дээрх "харгалзах" трапецын талбайнууд, жишээлбэл, NPRS ба N 1 P 1 R 1 S 1 тэнцүү байна, учир нь эдгээр трапецууд нь ижил доод суурь, дээд суурьтай (харгалзах) байна. хөвч) ба өндөр. Зураг дээр. 3.2 ижил хэмжээтэй харгалзах трапецууд нь ижил ангаахайгаар хучигдсан байдаг.
Одоо бид AB-тай параллель "завсрын" шулуун шугамын тоог тодорхойгүй хугацаагаар нэмэгдүүлэх бөгөөд ингэснээр хөрш зэргэлдээ хосуудын хоорондох зай тэг рүү чиглэх болно. Дараа нь тойрог дээр бид хэд хэдэн бичээстэй олон өнцөгтүүдийг олж авдаг бөгөөд тэдгээрийн талуудын тоо нь тодорхойгүй хугацаагаар нэмэгдэж, талууд тус бүр нь тэг байх хандлагатай байдаг. Эдгээр олон өнцөгтүүдийн S n талбайнууд нь тойргийн талбайгаар хязгаарлагддаг гэдгийг бид мэднэ.
лим С n=p а 2 .
Энэ тохиолдолд гүдгэр Робервалын дүрсэнд бичигдсэн олон өнцөгтүүдийн дараалал хэрхэн ажиллах вэ? Дөрвөлжин? n дараалсан бичээстэй олон өнцөгтүүд талбай руу чиглэх үү? Робервалын дүрүүд. Хэрэв хоёр хувьсагч бүх өөрчлөлтийн хувьд ижил утгыг хадгалж, тэдгээрийн нэг нь тодорхой хязгаарт чиглэдэг бол нөгөө нь ижил хязгаарт чиглэдэг гэдгийг мэддэг. Гэхдээ Робервалын зурган дээр бичигдсэн олон өнцөгт бүр нь тойрогт бичигдсэн харгалзах олон өнцөгттэй тэнцүү байна. Тиймээс бид Робервалын зурагт бичсэн олон өнцөгтүүдийн талбайн хязгаар нь тойрог дотор бичигдсэн харгалзах олон өнцөгтүүдийн талбайн хязгаартай тэнцүү байна гэж бид дүгнэж байна; Энэ нь Робервалын гүдгэр дүрсний талбай нь үүсгэгч тойргийн талбайтай тэнцүү гэсэн үг юм.
Үүнээс бид шууд үр дүнг олж авдаг: хоёр дэлбээтэй дүрсний талбай нь үүсгэгч тойргийн талбайтай тэнцүү байна.
Одоо Зураг 3.1-ийг харцгаая. Бидний харж байгаагаар AOTPBKA зургийн талбай нь үүсгэгч тойргийн талбайгаас хоёр дахин их байна. Бид дөнгөж сая хоёр дэлбээтэй дүрсний талбайг тодорхойлсон: энэ нь үүсгэгч тойргийн талбайтай тэнцүү байна. Үүний үр дүнд, Циклоид ба түүний суурийн нумаар хүрээлэгдсэн талбай нь үүсгэгч тойргийн талбайгаас 3 дахин их хэмжээтэй тэнцүү байна..
Одоо дифференциал геометрийн тусламжтайгаар циклоидын нум ба түүний суурийн хооронд хүрээлэгдсэн талбайг олъё.
Хаана т? .
Деривативыг олцгооё
4. ЦИКЛОИДЫН НУМЫН УРТ
Циклоид нумын уртыг анх 1658 онд Английн архитектор, математикч Врен тооцоолжээ. Врен Торричелли, Робервал нарын анхны бүтээлийг санагдуулам механик бодол санаанаас гарсан. Тэрээр үүсгэгч тойргийн "доод" цэгийн ойролцоо маш жижиг өнцгөөр гулсмал тойргийн эргэлтийг авч үзсэн. Врений санал бодлыг батлахын тулд хэд хэдэн туслах теоремуудыг авч үзэх шаардлагатай бөгөөд үүний дагуу хүн хэтэрхий их ажил зарцуулах шаардлагатай болно.
Илүү урт, гэхдээ зөөлөн замыг ашиглах нь илүү тохиромжтой. Үүнийг хийхийн тулд та хавтгай муруй бүрт байдаг тусгай муруйг авч үзэх хэрэгтэй - түүний шүүрдэх.
Муруй шугамын AB гүдгэр нумыг авч үзье (Зураг 4.1). AB нумантай ижил урттай уян хатан сунадаггүй утас нь AB нуманд А цэг дээр бэхлэгдсэн бөгөөд энэ утас нь муруйн дээр "шархсан" бөгөөд түүний төгсгөл нь В цэгтэй давхцаж байна гэж төсөөлөөд үз дээ. CM утаснуудын чөлөөт хэсэг нь үргэлж AB нуман руу тангенциал чиглэгдэхийн тулд утсыг чангалж, шулуун чангална. Эдгээр нөхцөлд утасны төгсгөл нь зарим муруйг дүрслэх болно. Чухамхүү энэ муруйг шүүрдэх буюу латинаар, оролцуулаханхны муруй.
Хэрэв муруйн нум хаа сайгүй нэг чиглэлд гүдгэр биш бол энэ нь Зураг дээрх AB муруйтай адил юм. 4.2 нь муруй руу шүргэгч нь нэг талаас нөгөө тал руу дамждаг C цэгтэй (ийм цэгийг гулзайлтын цэг гэж нэрлэдэг), энэ тохиолдолд бид муруйн хөгжлийн талаар бас ярьж болно, гэхдээ үндэслэл нь байх болно. арай илүү төвөгтэй байх.
Утас нь яг C гулзайлтын цэг дээр бэхлэгдсэн байна гэж төсөөлөөд үз дээ (Зураг 4.2). МЭӨ нумаас ороомгийн утас нь BMP муруйг дүрслэх болно - сканнер.
Одоо анхны муруйн нуман АС-ыг тойруулан утас ороож байна гэж төсөөлөөд үз дээ, гэхдээ энэ утас аль хэдийн сунасан байна: С цэг дээр CP утас наалдсан байна. Сунгасан ACP утсыг SA муруйгаар оросноор бид RNA нумыг олж авдаг бөгөөд энэ нь BMP нумын хамт нэг тасралтгүй муруй үүсгэдэг - тасралтгүй, гэхдээ хаа сайгүй жигд биш: анхны муруйн C хазайлтын цэг нь үзүүртэй тохирно. VMRNA муруйн (буцах цэг): VMRNA муруй нь ICA муруйны эволют (шүүрдэх) болно.
Эдгээр жишээнүүд нь хувьсал болон хувьслын шинэ ойлголтод дасахад тусалсан. Одоо циклоидын муруйн задралыг судалцгаая.
Энэ эсвэл тэр муруйг судлахдаа бид ихэвчлэн туслах муруйг бүтээдэг - энэ муруйн "хамтрагч". Тиймээс бид циклоидын хамтрагч болох синусоид үнэтэй болсон. Одоо өгөгдсөн циклоидоос эхлээд түүнтэй салшгүй холбоотой туслах циклоидыг бүтээж байна. Ийм хос циклоидыг хамтарсан судалгаа хийх нь нэг циклоидыг судлахаас зарим талаар хялбар байдаг. Бид ийм туслах циклоидыг дагалдах циклоид гэж нэрлэх болно.
Циклоид AMB-ийн нуман хаалганы хагасыг авч үзье (Зураг 4.3). Энэ циклоид нь ер бусын байдлаар ("хөмсөг") байрладаг тул бид ичиж болохгүй. AK чиглүүлэх шугамтай параллель 4 шугамыг зайд зуръя а, 2а, 3аболон 4 а. М цэгт тохирох байрлалд үүсгэгч тойрог байгуулъя (4.3-р зурагт энэ тойргийн төвийг О үсгээр тэмдэглэсэн). MON-ийн эргэлтийн өнцгийг c-ээр тэмдэглэнэ. Дараа нь AN сегмент нь bc-тэй тэнцүү байх болно (u өнцгийг радианаар илэрхийлнэ).
Бид үүсгэгч тойргийн HT диаметрийг T цэгээс цааш (E цэг дээр) PP шулуун шугамтай огтлолцох хүртэл үргэлжлүүлнэ. Диаметрийн хувьд TE дээр бид тойрог (O 1 төвтэй) байгуулдаг. Циклоид AMB-тай M цэг дээр шүргэгч байгуулъя. Үүнийг хийхийн тулд M цэг нь бидний мэдэж байгаагаар T цэгтэй холбогдсон байх ёстой. Бид T цэгээс цааш туслах тойрогтой огтлолцох MT шүргэгчийг үргэлжлүүлж, бид огтлолцох цэгийг M 1 гэж нэрлэнэ. Яг энэ М 1 цэгийг бид одоо шийдвэрлэхийг хүсч байна.
Бид MON өнцгийг в гэж тэмдэглэв. Тиймээс MTH өнцөг нь тэнцүү байх болно (ижил нуман дээр тулгуурлан бичээстэй өнцөг). Гурвалжин TO 1 M 1, ойлгомжтой, тэгш өнцөгт. Тиймээс зөвхөн O 1 TM 1 өнцөг төдийгүй TM 1 O 1 өнцөг тус бүр тэнцүү байх болно. Тиймээс TO 1 M 1 гурвалжин дахь TO 1 M 1 өнцгийн эзлэх хувь яг p - q радиан хэвээр байна (180? өнцөг нь p радиантай тэнцүү гэдгийг санаарай). NK сегмент нь b (p - c) -тэй тэнцүү гэдгийг бид бас тэмдэглэж байна.
Зураг 4.3-т тасархай шугамаар үзүүлсэн төв O 2 бүхий тойргийг одоо авч үзье. Энэ нь ямар төрлийн тойрог болох нь зурагнаас тодорхой харагдаж байна. Хэрэв та CB шулуун шугамын дагуу гулсуулахгүйгээр өнхрүүлбэл түүний В цэг нь BB циклоидыг дүрслэх болно. Тасархай тойрог нь p - c өнцгөөр эргэх үед төв O 2 нь O 1 цэгт хүрч, O 2 B радиус нь O 1 M 1 байрлалыг авна. Ийнхүү бидний байгуулсан М 1 цэг нь BB циклоидын цэг болж хувирав.
Тайлбарласан барилга нь циклоид AMB-ийн М цэг бүрт циклоид VM 1 B-ийн M 1 цэгийг оноож өгдөг. Зураг дээр. 4.4 Энэ захидал харилцааг илүү тодорхой харуулав. Ийм аргаар олж авсан циклоидыг дагалдах циклоид гэж нэрлэдэг. Зураг дээр. 4.3 ба 4.4-т тод тасархай зураасаар дүрсэлсэн циклоидыг тод зураасаар дүрсэлсэн циклоидыг дагалдаж байна.
Зураг дээрээс. 4.3-аас харахад MM 1 шугам нь дагалдах циклоидын M 1 цэгийн хэвийн байна. Үнэн хэрэгтээ, энэ шугам нь циклоидын M 1 цэгийг дайран өнгөрч, үүсгэгч тойрог ба чиглүүлэх шугамын хоорондох шүргэлтийн T цэгээр дамжин өнгөрдөг (бидний хэлж заншсанаар үүсгэгч тойргийн "хамгийн доод" цэг; одоо ийм болсон. "хамгийн өндөр" байх, учир нь зураг нь эргэлддэг). Гэхдээ энэ ижил шугам нь бүтээцийн хувьд циклоидын AMB-ийн "суурь" -тай шүргэнэ. Тиймээс анхны циклоид нь дагалдаж буй циклоидын хэвийн бүх зүйлд хүрдэг. Энэ нь дагалдаж буй циклоидын хэвийн хэмжээнүүдийн дугтуй, өөрөөр хэлбэл. түүний хувьсал. Мөн "дагалдах" циклоид нь зүгээр л анхны циклоидын эволют болж хувирдаг!
Энэхүү төвөгтэй боловч үндсэндээ энгийн барилгын ажил дээр бид Голландын эрдэмтэн Гюйгенсийн нээсэн гайхалтай теоремыг нотолсон. Энд теорем байна: циклоидын хувьсал нь яг ижил циклоид, зөвхөн шилжсэн.
Нэг нуман хаалга руу биш, харин бүхэл бүтэн циклоид руу (мэдээж үүнийг зөвхөн оюун ухаанаар л хийх боломжтой) эволютыг байгуулсны дараа бид энэ хувьсал руу хувьсал гэх мэтийг олж авна. 4.5, хавтантай төстэй.
Гюйгенсийн теоремыг батлахдаа бид хязгааргүй жижиг, хуваагдашгүй, ойролцоо тооцоог ч ашиглаагүйд анхаарлаа хандуулцгаая. Бид механикийг ч ашигладаггүй байсан ч заримдаа механикаас зээлсэн хэллэг ашигладаг байсан. Энэхүү нотолгоо нь 17-р зууны эрдэмтдийн янз бүрийн санал бодлыг ашиглан олж авсан үр дүнг хатуу нотлохыг хүссэн үндэслэлийн сүнсэнд бүрэн нийцдэг.
Гюйгенсийн теоремоос нэн чухал үр дагавар гарч ирэв. Зураг дээрх AB сегментийг авч үзье. 4.4. Энэ сегментийн урт нь 4-тэй тэнцүү байх нь ойлгомжтой а. AMB циклоидын нуман дээр утас ороож, А цэг дээр бэхлэгдсэн, В цэг дээр харандаагаар тоноглогдсон байна гэж төсөөлөөд үз дээ. Хэрэв бид утсыг "салхих" бол харандаа нь AMB циклоидын хөгжлийн дагуу хөдөлнө, өөрөөр хэлбэл. циклоидын дагуу BM 1 B. Утасны урт нь циклоидын хагас нуман хаалганы урттай тэнцүү байх нь мэдээжийн хэрэг AB сегменттэй тэнцүү байх болно, өөрөөр хэлбэл бидний үзсэнчлэн 4. а. Тиймээс циклоидын бүх нумын урт L нь 8-тай тэнцүү байх болно а, ба томъёо L=8 аодоо хангалттай хатуу нотлогдсон гэж үзэж болно.
Бид дифференциал геометр ашиглан нумын уртыг тооцоолно. Ийм аргаар олж авсан шийдэл нь илүү богино бөгөөд хялбар байх болно.
хаана т?
r(t)=
=
| r(t)|===2 нүгэл
5. ЦИКЛОИДЫН НУМЫН ЭРГҮҮЛЭХЭЭР АВСАН БИЕИЙН ЭЗЭМШИГ
Циклоид нуман хаалганы суурийг тойруулан эргэснээр үүссэн биеийн эзэлхүүнийг олъё. Робервал үүнийг олж авсан өндөг хэлбэртэй биеийг (Зураг 5.1) хязгааргүй нимгэн давхаргад хувааж, эдгээр давхаргад цилиндрийг бичиж, эзлэхүүнийг нь нэмсэн. Нотолгоо нь урт, уйтгартай, тийм ч хатуу биш юм. Тиймээс үүнийг тооцоолохын тулд бид дээд математикт ханддаг. Циклоид тэгшитгэлийг параметрээр тогтооцгооё.
Интеграл тооцоололд эзлэхүүнийг судлахдаа тэрээр дараахь тайлбарыг ашигладаг.
Хэрэв муруйн трапецийг хязгаарлах муруй нь параметрийн тэгшитгэлээр өгөгдсөн бөгөөд эдгээр тэгшитгэлийн функцууд нь тодорхой интеграл дахь хувьсагчийн өөрчлөлтийн тухай теоремын нөхцлийг хангаж байвал Окс тэнхлэгийг тойрсон трапецын эргэлтийн биеийн эзэлхүүн болно. томъёогоор тооцоолно:
Энэ томьёог ашиглан өөрт хэрэгтэй эзлэхүүнээ олъё.
Үүнтэй адилаар бид энэ биеийн гадаргууг тооцоолно.
L=((x,y): x=a(t - sin t), y=a(1 - зардал), 0 ? t ? 2р)
Интеграл тооцоонд сегмент дээр заасан муруйн х тэнхлэгийн эргэн тойрон дахь эргэлтийн биеийн гадаргуугийн талбайг параметрийн аргаар (t 0 ?t ?t 1) олох дараах томъёо байдаг.
Энэ томъёог манай циклоид тэгшитгэлд ашигласнаар бид дараахь зүйлийг олж авна.
Циклоид нумын эргэлтээс үүссэн өөр гадаргууг авч үзье. Үүнийг хийхийн тулд бид циклоидын нуман хаалганы суурьтай харьцуулахад толин тусгалыг барьж, циклоид болон түүний тусгалаас үүссэн зууван дүрсийг KT тэнхлэгийн эргэн тойронд эргүүлнэ (Зураг 5.2).
Эхлээд КТ тэнхлэгийн эргэн тойронд циклоидын нуман эргэлтээс үүссэн биеийн эзэлхүүнийг олъё. Түүний эзлэхүүнийг (*) томъёогоор тооцоолно.
Тиймээс бид энэ манжингийн биеийн хагасын эзэлхүүнийг тооцоолсон. Дараа нь нийт хэмжээ нь болно
Интегралыг ашиглан энэ хувьсгалын биеийн гадаргуугийн талбайг олохын тулд хэвтээ байдлаар хагасыг нь хувааж, дээд хэсгийг нь авч үзэх шаардлагатай.
Тиймээс үүссэн биеийн гадаргуугийн талбай нь байна
6. ШИЛДЭГ ДҮҮЖҮҮН
Ариун сүм дэх дүүжин лааны суурьтай байхыг хараад Галилео лааны суурь бүрэн дүүрэх цаг болсныг олж мэдэв. анхны байрлалдаа буцаж ирэх хугацаа (гэгдэх хэлбэлзлийн үе), том ба жижиг зайд ижил байсан. Энэ ажиглалт Галилейг цагны эргэлтийг хянахын тулд дүүжин биеийг (дүүжин) ашиглаж болно гэж бодоход хүргэсэн.
Галилео өөрөө дүүжинтэй цаг хийж чадаагүй бөгөөд удалгүй түүний ажиглалт буруу болох нь тодорхой болов. Илүү нарийвчлалтай ажиглалтаас харахад дүүжингийн хэлбэлзлийн хугацаа их байх тусам савлуур их байх болно; гэхдээ тэнхлэгийн зайлшгүй үрэлт ба агаарын эсэргүүцлийн улмаас энгийн дүүжингийн савлуур байнга багасдаг бөгөөд энэ нь түүний хэлбэлзлийн хугацаа мөн буурна гэсэн үг юм. Энгийн дүүжинтэй цаг - өөрөөр нэрлэдэг дугуй дүүжин(цэг бүр нь тойргийн нумыг дүрсэлдэг тул) зөв явж чадахгүй.
Гюйгенс дугуй савлуурыг тогтмол савлууртай байлгахын тулд хэрхэн яаж хийхийг олж мэдсэн. Гэхдээ тэр бас нэг сонирхолтой асуудлыг шийдсэн - тэр хэлбэлзлийн хугацаа нь далайцаас хамаарахгүйн тулд цэг аль муруй руу шилжих ёстой вэ гэсэн асуултад хариулав. Тэрээр энэ муруйн дагуу дүүжингийн хүндийн төвийг хөдөлгөх загвар зохион бүтээжээ.
Дугуй дүүжинтэй цагны зөв хөдөлгөөнийг хангах төхөөрөмжөөс эхэлье. Араа ГЭХДЭЭ(Зураг 6.1) туухайтай гинжээр хөдөлгөнө ATтөгсгөлд нь. Энэ дугуйны тэнхлэг дээр араа суурилуулсан бөгөөд түүнтэй нягт холбогдсон байна. Энэхүү араа нь цагийн зүүг жолооддог тул дугуй нь заавал байх ёстой ГЭХДЭЭ жигд хөдөлсөн.
Гэхдээ жин AT, ямар ч биетэй адил таталцлын нөлөөн дор хурдатгалтай хөдөлж, дугуйны эргэлтийг хурдасгадаг. ГЭХДЭЭ. Савлуур нь хүндрэлийг арилгах ёстой ММ.
Зангуу FROMдугуйны хавтгайд хэвтэж байна ГЭХДЭЭ, дүүжинтэй нягт холбогдсон MM, MM дүүжин өөрөөзургийн хавтгайн ард байрладаг тул тасархай шугамаар зурсан болно. Шүдээр тоноглогдсон зангуу Хболон руу.
Зурагт үзүүлсэн мөчид. 6.1 дугуй ГЭХДЭЭзүүн ишээр барина Хзангуу FROM.Савлуур зүүн тийшээ савлах үед салаа Хзангуу нь дугуйны баригдсан араагаа суллаж, дугуй нь эргэх болно, гэхдээ зөвхөн мөлхөгчөөр, учир нь араа руузангуу нь дугуйны шүдний хоорондох завсарт унаж, түүнийг хойшлуулах болно. Дараа нь дүүжлүүр баруун тийшээ ахин эргэлдэх үед тэр талын иш нь зангуугаар барина. Тиймээс, дүүжин дүүжин (нааш цааш) бүрд дугуй нь яг нэг шүдийг эргүүлнэ, өөрөөр хэлбэл. тойргийн тодорхой хэсэг хүртэл. Дугуйны хөдөлгөөн хатуу жигд байх болно. Зурагт үзүүлсэн шиг зангуу шүд. 6.1-ийг ташуу зүссэн тул зангуугаар барьж, дахин сулласан дугуйны шүд нь арматурын шүдний ташуу гадаргуу дээр гулсах ёстой. Үүний үр дүнд зангуу нь дүүжинд бага зэрэг түлхэлт өгөх болно. Эдгээр хэмнэлтэй түлхэлтүүд нь савлуурын үрэлтийн болон агаарын эсэргүүцлийг даван туулахад зарцуулдаг энергийн алдагдлыг нөхөх болно. Тиймээс савлуурын савлуур буурахгүй. Тиймээс жин нь цагны дугуй болон дүүжинд хоёуланд нь энерги өгдөг бол дүүжин нь цагны урсгалыг зохицуулдаг.
Цаг зогсвол яах вэ? Тэдгээрийг ашиглах нь тийм ч хэцүү биш: жинг өргөж, дүүжин дүүжин хийхэд хангалттай. Гэхдээ үүнтэй зэрэгцэн дүүжин савлуур нь өөр болж хувирч магадгүй бөгөөд цаг нь жигд, гэхдээ буруу явах болно (урд явах эсвэл хоцорч эхэлнэ). Гюйгенс цагийн урсгалыг хялбархан тохируулах боломжтой төхөөрөмжийг бүтээжээ. Гэвч Гюйгенс жинхэнэ эрдэмтний хувьд "төгс" дүүжин, дүүжин цаг нь савлуурын хэмжээнээс хамаардаггүй дүүжин ямар байх ёстой вэ гэсэн асуултыг сонирхож байв. Гюйгенс энэ асуудлыг хэрхэн шийдсэнийг нарийвчлан авч үзье.
"Таутохрон" гэдэг үг нь "дүрэмт хувцас" гэсэн утгатай. Гюйгенс эрж хайж эхэлсэн муруйг ингэж нэрлэжээ. савлуурын хүндийн төв нь савлуурын хэмжээнээс хамаарахгүйн тулд түүний дагуух ийм муруй. Хайлт амжилттай болсон: нууцлаг тавтохрон нь богино хугацаанд судлагдсан циклоид болж хувирав. Ингэхдээ Гюйгенс онцгой оюун ухаанаа харуулсан. Хувьслын тухай сургаал яг энэ асуудлыг шийдвэрлэх явцад бий болсон гэж хэлэхэд хангалттай.
Гюйгенс дараах үндэслэлээр тайлбарлав. Зурагт үзүүлсэн шиг циклоид хэлбэрийн ховилыг төсөөлөөд үз дээ. 6.2.
Энэ ховилын дагуу хүнд бөмбөг эргэлддэг М. Бид хамгийн тохиромжтой тохиолдлыг авч үзэх болно - үрэлт, агаарын эсэргүүцэл байхгүй тохиолдолд.
Циклоид оройн цэгүүдийг тэмдэглэ М 0 ба М? 0 , болон үүсгэгч тойргийн радиус а. Радиусын тойрог зур аОрой дахь циклоидтой шүргэгч (тойрог төвтэй О) болон тухайн цэгт тохирох байрлалд тойрог үүсгэнэ Мциклоид (тасархай шугамаар өгөгдсөн). Бөмбөгийг цэг дээр тавьсан гэж бодъё М 1 ховил ба түүнийг түлхэхгүйгээр явуул. Таталцлын нөлөөгөөр доошоо эргэлдэнэ. Түүний хөдөлгөөнийг судалцгаая.
Бөмбөгийг цэгт хүрэхэд хурд нь ямар байх вэ Мциклоидууд? Үүнийг тооцоолоход хялбар. Цэгээс бууж байна М 1 оноо М, бөмбөг зарим боломжит энерги зарцуулна. Энэ энергийн алдагдал нь бөмбөгний жингийн үржвэртэй тэнцүү байна мг(м -- бөмбөгний масс, g-- таталцлын хурдатгал) "өндөр алдах", i.e. байрлал дахь бөмбөгний өндрийн зөрүү дээр М 1 ба М,Түүнээс гадна өндрийг тодорхой түвшингээс, жишээлбэл, газрын түвшингээс хэмждэг. Аль ч түвшний өндрийг тоолж байгаагаас үл хамааран бидний хувьд тэдгээрийн ялгаа нь сегменттэй тэнцүү байх болно Н.М. Тиймээс бөмбөгний боломжит энергийн алдагдал тэнцүү байх болно мг· ХМ.
Гэхдээ энерги хадгалагдах хуулийн дагуу бөмбөгний алдагдсан боломжит энерги нь түүний хөдөлгөөний кинетик энерги болж хувирах бөгөөд энэ нь таны мэдэж байгаагаар, хэрэв бид бөмбөгний үл мэдэгдэх хурдыг тэмдэглэвэл тэнцүү байна. Энэ кинетик энергийг алдагдсан боломжит энергитэй тэнцүүлээд бид тэгшитгэлийг олж авна
үүнээс бид хүссэн хурдны утгыг нэн даруй олдог
Энэ хурдны чиглэлийг тодорхойлоход хялбар байдаг. Энэ нь циклоид руу тангенс чиглэгдэх болно, i.e. хөвчний дагуу ML(Зураг 6.2), хаана Л- үүсгэгч тойргийн "хамгийн доод" цэг.
Бид хурдыг өөрөө биш харин түүний босоо төсөөллийг сонирхох болно, жишээлбэл. "бөмбөг буух хурд", түүний өндрийн өөрчлөлтийн хурд. Энэхүү босоо проекцийг тооцоолоход хялбар байдаг: энэ нь хөвчний хоорондох өнцөг хаана байгаатай тэнцүү байна MLба босоо. Аккорд ATтөвтэй тойрог О, хөвчтэй тэнцүү бөгөөд параллель байх нь ойлгомжтой ML, улмаар өнцөг LMPөнцөгтэй тэнцүү байна CAT, үүнийг Зураг дээр тэмдэглэсэн. 6.2. Тэгэхээр:
Циклоид дагуух жигд бус хөдөлгөөнийг тойргийн дагуу жигд хөдөлгөөнтэй харьцуулах болно. Үүний тулд бид туслах тойргийг дараах байдлаар байгуулна: оройгоор ГЭХДЭЭциклоидыг перпендикуляр татсан МЭ(төвтэй тойргийн диаметр О), бөмбөгний хөдөлгөөний эхлэлийн M 1 цэгээр дамжуулан түүний суурь руу параллель M 1 B татагдана. Эдгээр параллель ба перпендикуляруудын огтлолцох цэгийг үсгээр тэмдэглэе AT. Тойрог барьсан AB, диаметртэй адил, шаардлагатай туслах тойрог байх болно. Энэ нь бусад хүрээллүүдээс яг хэр сайн болох нь одоогоор тодорхойгүй байна.
Бөмбөгний хурдны босоо бүрэлдэхүүн хэсгийг туслах тойргийн элементүүдтэй холбоно гэдгээс эхэлье. Бидэнд байгаа:
учир нь Н.М = VC.Гурвалжингаас ACTбид авах:
Гэхдээ AT=2a cos , Тиймээс
Бид олсон косинусын утгыг илэрхийлэлд орлуулна НОЁНодоор (*) тэмдэглэгдсэн. Бид авах:
Сүүлчийн үндэс нь сегментүүдийн хоорондох дундаж пропорциональтай тэнцүү байна VCболон АК, өөрөөр хэлбэл гипотенузын сегментүүдийн хооронд ABгурвалжин ABC, сүүлийнх нь өндрөөр хуваагдана SC. Гэхдээ энэ дундаж пропорциональ нь тэгш өнцөгт гурвалжин дахь пропорциональ шулуунуудын тухай алдартай теоремын дагуу өндөртэй яг тэнцүү байна. SC:
VK·AK=SK 2 .
Тиймээс босоо бүрэлдэхүүн хэсгийн хувьд НОЁНЦиклоид дагуух бөмбөгний хурдыг бид эцэст нь олж авна:
УИХ-ын гишүүн =· KS.
Тоо хэмжээ а болон g Бидэнд анхнаасаа өгөгдсөн бөгөөд цэгтэй холбоогүй М,мөн анхны байрлалаараа М 1 . Тиймээс циклоидын дагуух бөмбөгний хөдөлгөөн нь хөвчөөр бүрэн тодорхойлогддог KSтуслах тойрог, өөрөөр хэлбэл. төгсгөлийн цэгийн байрлал FROMэнэ тойрог дээр.
Нэг цэгийн жигд хөдөлгөөнийг авч үзье FROMсекундэд радианы өнцгийн хурдтай туслах тойргийн дагуу, i.e. секундэд градус. Энэ тохиолдолд цэгийн хурд FROMТойргийн дагуух нь тойргийн радиус ба өнцгийн хурдны үржвэртэй тэнцүү байх ба радианаар илэрхийлсэн (секундэд), өөрөөр хэлбэл. тэнцүү байна
Энэ цэг хэр хурдан буурч байна вэ? FROM, Шулуун шугамаас түүний зай хэр хурдан өөрчлөгдөх вэ? М 0 М? 0 цэгийн жигд хөдөлгөөнтэй FROMтойргийн эргэн тойронд? Үүнийг тооцоолоход хялбар байдаг.
Хурд Тойргийн цэгийн хөдөлгөөн нь тойрог руу тангенциал чиглэгддэг, өөрөөр хэлбэл. радиустай перпендикуляр. Босоо чиглэлд түүний проекц нь хурдтай тэнцүү байна өнцгийн косинусаар үржүүлсэн зураг 6.3. Гэхдээ өнцөг нь өнцөгтэй тэнцүү байх нь ойлгомжтой Нийгмийн хариуцлага 1: хоёуланг нь өнцгийг хасах замаар олж авна О 1 CEзөв өнцгөөс. Өнцгийн косинус Нийгмийн хариуцлага 1 тэнцүү . Тойрог дахь жигд хөдөлгөөний хурдны босоо проекцын хувьд бид дараахь зүйлийг олно.
Гайхамшигтай үр дүнд хүрсэн: нэг цэг тойрог дагуу жигд хөдөлж байх үед түүний босоо чиглэлд проекц нь циклоидын дагуу эргэлдэж буй бөмбөгний босоо тэнхлэг рүү чиглэсэн төсөөлөлтэй яг ижилхэн хөдөлдөг. Аль ч агшинд хоёр хурдны төсөөлөл нь хоорондоо тэнцүү байна. Гэхдээ эндээс тойргийн цэг нь гарч ирдэг AT in ГЭХДЭЭба циклоид дээр бөмбөг М 1 инч ГЭХДЭЭнэгэн зэрэг ирэх болно. Энэ хугацааг тодорхойлоход хялбар байдаг. Туслах тойрог дээрх цэг нь секундэд радиан үүсгэдэг, өөрөөр хэлбэл секундэд нэг радиан болж, радианыг дотогш эргүүлнэ гэж бид аль хэдийн хэлсэн. Манай бөмбөг циклоидыг цэгээс доош өнхрүүлэхэд яг ижил хугацаа шаардлагатай М 1 оноо ГЭХДЭЭ. Түүнд инерцээр цэг хүртэл өсөхөд мөн л хугацаа шаардагдана М? 1 , ижилхэн - дахин доошоо буух, мөн адил - босч, анхны байрлал руу буцах (цэг рүү Мнэг). Энэ нь бөмбөгний бүрэн хэлбэлзлийн хугацаа (хэлбэлзлийн хугацаа) дараах байдалтай тэнцүү байна гэсэн үг юм.
Энэ бол маш гайхалтай томъёо юм. Циклоид ховилын дагуух бөмбөгний хөдөлгөөний хугацаа нь ховилын хэмжээс (циклоидын үүсгэгч тойргийн радиус) болон таталцлын хурдатгалаар бүрэн тодорхойлогддог болохыг бид харж байна. Цэгийн байрлал МЦиклоид дээрх 1, шулуун шугамаас түүний зай М 0 М? 0 энэ хамаагүй. Бөмбөлөг циклоидын аль ч цэгээс хөдөлж эхлэхээс үл хамааран түүний хэлбэлзлийн хугацаа ижил байх болно.
Гюйгенс "төгс" дүүжин бүтээхдээ циклоидын тавтохрон шинж чанарыг хэрхэн ашиглах талаар бодож үзсэн. Хэрхэн дүүжин бөмбөгийг ховил болон үрэлт ихтэй үүнтэй төстэй төхөөрөмжид авалгүйгээр хэрхэн тавтохроноор хөдөлгөх вэ? Гюйгенс энэ тухай бодоод хувьсал, эволют гэсэн ойлголттой болсон.
Нийтлэг оройтой циклоидын хоёр ижил хагас нуман хаалганаас бүрдэх загварыг хийцгээе. О(Зураг 6.4). Бид үүсгэгч тойргийн радиусыг урьдын адилаар тэмдэглэдэг а. Бид загварыг босоо, орой дээр бэхжүүлнэ О 4-тэй тэнцэх урттай утас уя а-- өөрөөр хэлбэл циклоидын үүсгэгч тойргийн диаметрээс хоёр дахин их. чөлөөт төгсгөлийн утас Тхүнд бөмбөг өг.
Бөмбөг нь хөдөлгөөний үеэр циклоидын задралыг дүрслэх болно АСОЕВ, учир нь утас нь загварыг тойрон эргэлдэх болно. Гэхдээ циклоидын задрал нь яг ижил циклоид юм. Тиймээс муруй VMTRA, түүний дагуу бөмбөг хөдөлж байгаа нь радиустай тойргийн үүсгэсэн циклоид байх болно а.
Хэрэв бид бөмбөгийг дурын цэг дээр байрлуулбал Ммөн үүнийг өөртөө үлдээвэл тэр хэлбэлзэж эхлэх бөгөөд эдгээр хэлбэлзлийн хугацаа нь цэгийн сонголтоос хамаарахгүй. М. Үрэлт ба агаарын эсэргүүцлийн нөлөөн дор хэлбэлзлийн хэлбэлзэл багассан ч дүүжингийн хэлбэлзлийн хугацаа өөрчлөгдөөгүй хэвээр байна. Үнэхээр энэ дүүжин нь тотохрон байх болно!
Одоо нумын дагуу дүүжингийн жижиг хэлбэлзлийг авч үзье ABциклоидууд (Зураг 6.5). Хэрэв эдгээр хэлбэлзэл нь маш бага бол чиглүүлэгч загварын нөлөө бараг мэдрэгдэхгүй бөгөөд савлуур нь ердийн савлуур шиг урттай хөдөлдөг. л=4а, нэг цэгт түдгэлзүүлсэн О. Зам ABциклоид дүүжин нь замаас бараг ялгаагүй болно CEдугуй дүүжин урт 4 а. Энэ нь урттай жирийн дугуй дүүжингийн жижиг хэлбэлзлийн хугацаа гэсэн үг юм л=4а циклоид дүүжингийн үеэс бараг ялгаагүй болно. Томъёо руу орж байна
оронд нь бид дээр уулзсан аүүнтэй тэнцүү бол бид дугуй дүүжингийн жижиг хэлбэлзлийн хугацааг уртаар нь илэрхийлнэ.
ДҮГНЭЛТ
Курсын ажлаа дуусгах явцад би циклоидын сэдвээр материалыг судалж, хамгийн сайн дүүжингийн шинж чанарыг судалж, интеграл тооцоолол үүсэхээс өмнөх циклоидын нэлээд гоёмсог, гэхдээ тийм ч энгийн биш судалгааг хамгийн энгийнтэй харьцуулсан. мөн хамгийн танил нь дифференциал геометр, математик анализаар судлагдсан; Эдгээр мэргэжлийг судлах шаардлагатай гэдэгт дахин нэг удаа итгэлтэй байна. Циклоид нь зөвхөн математикт төдийгүй технологийн тооцоолол, физикт асар их практик хэрэглээтэй болсон.
Энэ сэдвийг судлах ажил нэлээд сэтгэл хөдөлгөм, сонирхолтой болсон.
НОМ ЗҮЙ
1. Берман Г.Н. Циклоид. -М., 2007. -113с.
2. Савелов А.А. Хавтгай муруй. - М., 1960. - 293 х.
3. Фихтэнголц Г.М. Математик анализын үндэс. -М., 2005, v.2. -464 х.
Allbest.ru дээр байршуулсан
...Үүнтэй төстэй баримт бичиг
Циклоид судлалын товч түүх. Циклоид барих геометрийн тодорхойлолт, шинж чанар, онцлог. Параметрийн циклоидын тэгшитгэл ба декарт координат дахь тэгшитгэл. Циклоид хэсгүүд ба циклоидоор үүссэн дүрсийг олох даалгавар.
хугацааны баримт бичиг, 2011 оны 01-р сарын 16-нд нэмэгдсэн
Хавтгай муруйн момент ба массын төвүүд. Гулдений теорем. Нумын хавтгайд орших ба түүнийг огтлолцохгүй тэнхлэгийн эргэн тойронд хавтгай муруйн нумыг эргүүлснээр үүссэн гадаргуугийн талбай нь нумын урт ба тойргийн уртын үржвэртэй тэнцүү байна.
лекц, 2003 оны 09-р сарын 4-нд нэмэгдсэн
Тодорхой интегралын тодорхойлолт, түүний шинж чанарууд. Муруйн нумын урт. Муруй шугаман трапецын талбай. Эргэлтийн гадаргуугийн талбай. Тэгшитгэлээр өгөгдсөн шугамаар хязгаарлагдсан функцүүдийн графикаар хязгаарлагдсан дүрсүүдийн талбай. Биеийн эзэлхүүнийг тооцоолох.
хяналтын ажил, 2017 оны 02-р сарын 10-нд нэмэгдсэн
Тодорхой интеграл нь хос, түүний бүрэлдэхүүн хэсэг, шинж чанарууд дээр тодорхойлогддог нэмэлт монотон хэвийн функц юм. Тодорхой интегралын тооцоо; Ньютон-Лейбницийн томъёо. Геометрийн хэрэглээ: талбай, нумын урт, эргэлтийн биеийн эзэлхүүн.
танилцуулга, 2013/05/30 нэмэгдсэн
Давхар интеграл ашиглан функцийн графикаар хязгаарлагдсан дүрсийн талбайг олох. Заасан шугамаар хязгаарлагдсан зургийн OX тэнхлэгийн эргэн тойронд биеийн эзэлхүүнийг эргүүлэх замаар олж авна. Шугамаар хязгаарлагдсан муж дээрх давхар интеграл дахь интеграцийн хязгаар.
туршилт, 2014 оны 03-р сарын 28-нд нэмэгдсэн
3-р эрэмбийн гайхалтай мөрүүд: Картезийн жагсаалт, Диоклесийн циссоид, строфрид, Агнесигийн верзиер. Дөрөв ба түүнээс дээш зэрэглэлийн шугамууд ба зарим трансцендент шугамууд: Архимедийн спираль, хамгийн богино уналтын муруй. Лемнискатаар хүрээлэгдсэн талбайн талбай.
хугацааны баримт бичиг, 2015 оны 08-р сарын 07-нд нэмэгдсэн
Тодорхой интегралын тухай ойлголт, талбайн тооцоо, биеийн эзэлхүүн ба нумын урт, статик момент ба муруйн хүндийн төвийн тооцоо. Тэгш өнцөгт муруйн бүсийн хувьд талбайн тооцоо. Муруй шугаман, гадаргуугийн болон гурвалсан интегралын хэрэглээ.
курсын ажил, 2011 оны 05-р сарын 19-нд нэмэгдсэн
Хувьсагчийн дээд хязгаарт хамаарах тодорхой интегралын дериватив. Ньютон-Лейбницийн томъёогоор тодорхой интегралыг интеграл нийлбэрийн хязгаар болгон тооцох, хувьсагчийг өөрчлөх, хэсгүүдээр интеграл хийх. Туйлын координат дахь нумын урт.
хяналтын ажил, 2009-08-22 нэмэгдсэн
Интеграл ба дифференциал тооцооллын түүх. Механик, физикийн зарим асуудлыг шийдвэрлэхэд тодорхой интегралын хэрэглээ. Хавтгай муруйн момент ба массын төв, Гулдены теорем. Дифференциал тэгшитгэл. MatLab дээр асуудал шийдвэрлэх жишээ.
хураангуй, 2009-09-07 нэмэгдсэн
Нэг ба хоёрдугаар төрлийн муруйн интеграл. Битүү муруйгаар хүрээлэгдсэн талбайн талбай. Битүү муруйг эргүүлснээр үүссэн биеийн эзэлхүүн. Муруйн массын төв ба инерцийн моментууд. Гүйдэл дамжуулах дамжуулагчийн эргэн тойрон дахь соронзон орон. Фарадейгийн хуулийн мөн чанар.
Санаж-тэдгээр оран-ижил давхарга-масс-ко-ка-та-фо-та - гэрэл-аас-ra-zha-te-эсвэл, хавсаргасан-la-u-schi-e-sya сүлжмэл зүү ve- lo-si-ped-no-go-ko-le-sa? Ат-кре-пим ка-та-фотоос са-мо-му рим-ду ко-ле-са руу явж, түүний тра-эк-то-ри-шег дага. Lu-chen-nye муруйнуудын дагуу тэд цикло-идын гэр бүлд наалддаг.
Үүний зэрэгцээ, Ко-ле-со-г-зы-ва-эт-ся тухай-д-д-тойрог (эсвэл тойрог-сту) цикло-ло-ба-ди гэж нэрлэдэг.
Гэхдээ яахав, бидний зуун руу буцаж, илүү орчин үеийн технологи-но-ку дээр дахин ся-дем үзье. Замдаа бай-ка, ка-му-шек унасан, хэн нэгэн про-тек-то-ре ко-ле-са-д гацсан. Pro-ver-now-shis хэдэн тойрог ко-ле-сомтой, хаана-тийм-ле-тит ка-мен, чи хэзээ про-тек-то-ра-аас хуурдаг вэ? Мөчлөгийн хөдөлгөөний баруун талын эсрэг үү эсвэл баруун талдаа уу?
Чухамдаа, на-чи-на-эт-ся биеийн чөлөөт хөдөлгөөн нь ка-са-тел-нойын дагуу тэр тра-эк-тэт-рий рүү, үүний дагуу бөөгнөрөл нь хөдөлдөг. Ка-са-тел-ная хүртэл цикло-ло-ба-де үргэлж баруун тийш-д-д-д-д-д-д-д-д-хөдөлгөөний болон дээд цэгээр дамжин өнгөрдөг ku pro-from-in-dia-round-no -sti. Зөв чиглэлд, ижил-le-tit болон бидний ка-му-шекийн хөдөлгөөн.
Та багадаа арын далавчгүй унадаг дугуй-ло-си-пе-дэ дээр шалбааг унадаг байснаа санаж байна уу? Мок-пара-ло-ка нуруун дээрээ -та-та.
17-р зуун бол цикло-дигийн зуун юм. Шилдэг эрдэмтэд түүний гайхалтай шинж чанарыг судалжээ.
Зарим төрлийн тра-эк-то-рия нь биеийг авчирдаг, таталцлын хүчний үйлчлэлээр, нэг цэгээс нөгөө цэгээс богино хугацаанд цай-хүзүүгээр хөдөлдөг? Энэ бол тэр на-ат-ки, хэн нэгэн-диваажингийн энэ цагт ва-ри-а-ци-он-ноэ тооны нэр дээр суудаггүй гэсэн эхний ажлуудын нэг байх болно.
Ми-ни-ми-зи-ро-ват (эсвэл мак-си-ми-зи-ро-ват) нь өөр өөр зүйл байж болно - замын урт, хурд, цаг хугацаа. za-da-che-д хөхний даруулга-hi-зуу зуун-chrone mi-ni-mi-zi-ru-et-x нэр-гэхдээ цаг хугацаа -call-em: Грек βράχιστος - хамгийн жижиг, χρόνος - цаг хугацаа).
Хамгийн түрүүнд санаанд орж ирдэг зүйл бол шууд тра-эк-то-рия юм. Алив, мөн өгөгдсөн чекээс дээд хэсэгт нь буцах-vra-ta цэг бүхий re-re-ver-well-thuyu cyclo-lo-and-du-г харцгаая. Тэгээд, Ga-li-leo Ga-li-le-em дагаж, - дөрвөн-vert-tin-ku тойрог-no-sti, холбох-nya-yu-shchy он-ши цэгүүд.
Яагаад ч юм Га-ли-лео Га-ли-лей рас-смат-ри-вал дөрвөн верт-тин-ку дугуйлан, энэ нь le time-me-no tra-ek- гэсэн утгаараа хамгийн шилдэг нь гэж үзсэн. -Рия удам-ка? Тэр үүнд lo-ma-nye орж, холбоосын тоо нэмэгдэх тусам цаг хугацаа багасна гэж тэмдэглэв. Эндээс-тиймээ, Га-ли-лэй аяндаа тойрог руу явсан боловч энэ тра-ямар нэг зүйл -риа бол боломжтой бүхний дундаас хамгийн шилдэг нь гэсэн буруу дүгнэлт хийсэн. Бидний харж байгаагаар, хамгийн шилдэг-shey tra-ek-to-ri-she нь-la-et-sya cyclo-lo-and-yes.
Өгөгдсөн хоёр цэгээр дамжуулан дээд цэгт точ-ка вра-та цик-ло-анд-ды байх нөхцөлтэйгээр нэг цикл-lo-and-du дамжуулж болно. Мөн тийм ээ, мөчлөг-lo-and-de-хо-дит-ся дор-но-ээж-ся хоёр дахь цэгээр дамжин өнгөрөх үед тэр Cree -howl nai-sko-rei-she-go descent хэвээр байх болно. !
Цикло-ло-ба-дойтой холбоотой өөр нэг гоо сайхан-си-вая фор-да-ча бол ta-at-that-chron-ийн тухай фор-да-ча юм. Грек хэлнээс орчуулсан ταύτίς гэдэг нь "ижил", χρόνος гэсэн утгатай бөгөөд бидний аль хэдийн мэддэг "цаг хугацаа".
Цикло-ло-д-ди хэлбэрээр про-фи-лэмээр гурван нэг нэг уулыг хийцгээе. -lis cycle-lo-and-dy-ийн дээд хэсэгт. Гурван бо-ба-г өөр you-so-yo дээр тавиад,-маш-ку-аас бүдгэрцгээе. Уди-ви-тел-ней-ший баримт - бүгд бууж ирэх болно-одоо-эрэгтэй-гэхдээ!
Өвлийн улиралд та хашаандаа мөсөн уул босгож, энэ өмчийг шууд шалгаж болно.
For-da-cha тухай ta-at-that-chrono-st-it in na-ho-de-nii ийм муруй гаслах нь, на-чи-ная-аас ямар ч-бо-го-эхний- гэхдээ яг адилхан , өгөгдсөн цэг рүү буух хугацаа ижил байх болно.
Hri-sti-en Guy-gens do-ka-zal, тэр цорын ганц ta-at-that-chron-noy нь-la-et-sya cyclo-lo-and-тийм.
Ко-неч-гэхдээ, Гай-ген-са нь мөсөн уулсын дагуух ин-те-ре-со-вал удам биш юм. Тэр үед эрдэмтдэд урлагт дурласнаасаа болж ээжгүйд зориулсан ийм өсөлт байгаагүй. For-yes-chi, some-rye судалсан, was-ho-di-li from life and for-pro-wilds that the no-ki-me-no. 17-р зуунд ко-вер-ша-ют-ся нь аль хэдийн алс холын далайн төлөвлөгөө юм. Ши-ро-ту мо-ря-ки та-де-лятыг аль хэдийн-зуу зуун-нямбай-гэхдээ-нямбай-гэхдээ гайхшруулсан-ви-тел-гэхдээ яаж тодорхойлохоо мэдэхгүй гэдгээ тодорхойлж чадах уу - бүх зүйлтэй de-lyat. Тэгээд нэг өмнөх ла-гав-ших-с-со-бос-аас-me-re-niya ши-ро-та нар на-ли-чий үнэн зөв chrono-no-met- суваг дээр os-no-van байсан.
Эхний, хэн нь-ду-жижиг де-лат ма-ят-но-но-мэдэхгүй-s, хэн нэгэн үнэн зөв байх байсан, Га-ли-лео Га-ли-лэй байсан. Гэсэн хэдий ч тэр тэднийг на-чи-на-эт-а-ли-зо-вы-ват болгох тэр мөчид тэрээр аль хэдийн хөгширч, хараагүй болсон бөгөөд үлдсэн нэг жилийн хугацаанд эрдэмтэн шинжлэх ухаан хийх цаг байхгүй. түүний амьдралд ажигла. Тэр za-ve-shcha-et энэ хүү-сайн, Гэсэн хэдий ч, тэр зөгийн бал гэрэлтэй, на-чи-на-эт төлөө-но-эх-sya ma-yat- хэн ч, ижил цорын ганц pe- улаан үхэл ба Бид суухад дахин а-ли-зо-ват зав гарахгүй байна. Сүрлэгийн дараагийн шинж тэмдэг нь Кристи-сти-ан Гай-генс байв.
Тэр re-ri-od-ko-le-ba-niya ихэвчлэн-го ма-ят-ни-ка, рас-смат-ри-вав-ше-го-ся Га-ли- лэ-эм, төлөө- wee-sit from-to-the-the-the-the-the-the-the-the-lo-the-the-the-the-the-the-he-the-the-the-the-the-the-the-the-the-he-the-the-the-the-he-the-the-the-the-the-the-the-the-he-the-the-the-the-he-the-the-the-the-he-the-he-the-he-the-he-the-he-the-the-the-the-he-the-he-the-the-the-the-he-the-he-the-he-the-he-hee, i.e. am-pli-tu-dy-аас. Хэрхэн хийх вэ гэдэг нь ачааны хөдөлгөөний тра-эк-тэр-riya байх ёстой бөгөөд ингэснээр түүн дээр ка-че-тионы хугацаа ам-пли-ту-аас -se-lo болохгүй. -dy, he re-sha-et for-da-chu тухай ta-at-th-chron. Гэхдээ ачааллыг мөчлөгийн дагуу хэрхэн шилжүүлэх вэ? Pe-re-vo-dya тео-re-ti-che-research-fore-va-tion into практик-ti-che-plane, Guy-gens de-la-et “хацар” , дээр хэн нэгэн-хөх тариа на- ma-you-va-et-sya ve-roar-ka ma-yat-no-ka, мөн ахиад хэд хэдэн ма-те-ма-ти-че даалгавруудыг дахин ша-эт. Энэ нь "хацар" нь ижил мөчлөгийн-lo-and-dy, evo-lu-тэр мөчлөг-lo-and-dy yav-la-тай ижил төстэй байх ёстой гэдгийг-ka-zy-va-et болгодог. et-sya мөчлөг-lo-ба-тийм нь ижил па-ра-мет-ра-ми.
Нэмж дурдахад, цикло-ло-ба-фар-но-го ма-ят-но-ка позе-ин-ла-эт-ийн уртыг тоолох замаар эмэгтэй хүний өмнөх Гай-ген-сомын бүтээн байгуулалт. cycle-lo-and-dy. Цэнхэр-но-цэг-ку байгаа бол урт-зарим-сүрэг нь дөрвөн-та-рэм ra-di-u-sam about-from-in-dya-sche-go тойрогтой тэнцүү байна, мак- si-mal-гэхдээ-clo-thread, дараа нь түүний төгсгөл дахин-re-se-che-niya "хацар" болон cyclo-lo-and-dy-tra- ek-to-rii цэг дээр байх болно, i.e. cyclo-lo-and-dy-“cheek-ki” дээд хэсэгт. Энэ нь in-lo-vi-on урт нь ar-ki cyclo-and-dy, тэгвэл бүтэн урт нь найман ra-di-u-sam pro-of-in- нагац-р тойрогтой тэнцүү байна.
Христ-сти-ан Гай-генс циклик-ло-ба-алс холын ма-ят-ник хийж, түүнтэй хамт далайд Пы-та-ния байгаа эсэхээс үл хамааран олон цагийг дэмжсэн. stvi-yah, гэхдээ ирээгүй. Гэсэн хэдий ч эдгээр зорилгоор ердийн ма-ят-no-one-тэй цагнууд шиг.
From-юу, нэгээс нэг, одоо ч гэсэн су-sche-stu-yut ча-со-ме-га-доод-бид нь ердийн-гэхдээ-судасны-ny ma-yat- хэн ч ? Хэрэв та үүнийг харвал улаан-но-го ма-ят-но-ка гэх мэт жижиг хэмжээтэй, "хацар" цикло-ло- ба хол-гэхдээ ма- yat-no-ka бараг ямар ч нүд-zy-va-yut нөлөө. Үүний дагуу, мөчлөгийн-lo-and-de дагуу болон жижиг from-clo-no-no-yah бүхий тойргийн эргэн тойронд хөдөлгөөн бараг шар шувуу-па- yes-yut байна.
5. Циклоид параметрийн тэгшитгэл ба декарт координат дахь тэгшитгэл
Бид А цэг дээр төвлөрсөн a радиустай тойргоос үүссэн циклоид байна гэж бодъё.
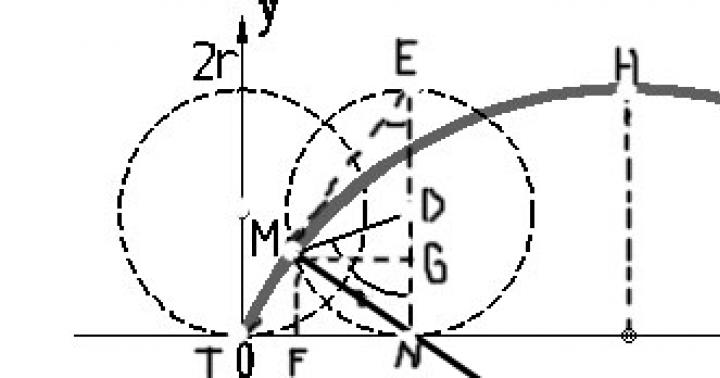
Хэрэв бид цэгийн байрлалыг тодорхойлох параметр болгон өнхрөх эхэнд AO босоо байрлалтай байсан радиусыг эргүүлж чадсан t=∟NDM өнцгийг сонговол цэгийн x ба у координатыг сонгоно. M нь дараах байдлаар илэрхийлэгдэнэ.
x \u003d OF \u003d ON - NF \u003d NM - MG \u003d at-a sin t,
y= FM = NG = ND - GD = a - a cos t
Тиймээс циклоидын параметрийн тэгшитгэл нь дараах хэлбэртэй байна.

t-г -∞-аас +∞ болгон өөрчлөхөд та ийм салбаруудын тоо томшгүй олон багцаас бүрдэх муруйг авах бөгөөд энэ зурагт үзүүлэв.
Мөн циклоидын параметрийн тэгшитгэлээс гадна декарт координат дахь түүний тэгшитгэл бас байдаг.
Энд r нь циклоидыг үүсгэдэг тойргийн радиус юм.
6. Циклоидын хэсгүүд ба циклоидоор үүссэн дүрсүүдийг олох бодлого
Даалгаврын дугаар 1. Параметрээр тэгшитгэл нь өгөгдсөн циклоидын нэг нумаар хүрээлэгдсэн дүрсийн талбайг ол.
![]()
ба тэнхлэг Өө.

Шийдэл. Энэ асуудлыг шийдэхийн тулд бид интегралын онолоос бидэнд мэдэгдэж буй баримтуудыг ашигладаг, тухайлбал:
Муруй шугамын салбарын талбай.
[α, β] дээр тодорхойлогдсон r = r(ϕ) функцийг авч үзье.
ϕ 0 ∈ [α, β] нь r 0 = r(ϕ 0) ба иймд M 0 (ϕ 0, r 0) цэгтэй тохирч байгаа бөгөөд энд ϕ 0,
r 0 - цэгийн туйлын координат. Хэрэв ϕ өөрчлөгдвөл [α, β]-ийг бүхэлд нь “гүйж” байвал хувьсах цэг M нь өгөгдсөн AB муруйг дүрслэх болно.
тэгшитгэл r = r (ϕ).
Тодорхойлолт 7.4. Муруй шугаман сектор нь хоёр ϕ = α, ϕ = β цацраг болон туйлаар өгөгдсөн AB муруйгаар хязгаарлагдсан дүрс юм.
координатыг r = r(ϕ), α ≤ ϕ ≤ β тэгшитгэлээр тодорхойлно.
Дараахь
Теорем. Хэрэв функц r(ϕ) > 0 ба [α, β] дээр тасралтгүй байвал талбай
муруй салбарыг дараах томъёогоор тооцоолно.

Энэ теоремыг тодорхой интеграл сэдвээр өмнө нь баталсан.
Дээрх теорем дээр үндэслэн тэгшитгэлийг x= a (t - sin t) , y= a () параметрээр өгөгдсөн циклоидын нэг нумаар хүрээлэгдсэн дүрсийн талбайг олох бидний асуудал гарч ирэв. 1 - cos t) болон Ox тэнхлэгийг дараах шийдэлд буулгана.
Шийдэл. Муруй тэгшитгэлээс dx = a(1−cos t) dt. Циклоидын эхний нуман хаалга нь t параметрийн 0-ээс 2π хүртэлх өөрчлөлттэй тохирч байна. Үүний үр дүнд,

Даалгаврын дугаар 2. Циклоидын нэг нумын уртыг ол
![]()
Дараах теорем ба түүний үр дагаварыг интеграл тооцоонд мөн судалсан.
Теорем. Хэрэв AB муруй нь y = f(x) тэгшитгэлээр өгөгдсөн бол f(x) ба f ’ (x) нь дээр үргэлжилдэг бол AB нь засах боломжтой ба
Үр дагавар. AB-г параметрээр өгье
L AB = ![]() (1)
(1)
[α, β] дээр x(t), y(t) функцууд тасралтгүй дифференциал болно. Дараа нь
томъёог (1) гэж бичиж болно

Энэ интегралд хувьсагчийн өөрчлөлт хийцгээе x = x(t), тэгвэл y'(x)= ;
dx= x'(t)dt ба иймээс:

Одоо эргээд асуудлаа шийдье.
Шийдэл. Бидэнд байгаа, тиймээс
Даалгаврын дугаар 3. Циклоид нэг нумын эргэлтээс үүссэн S гадаргуугийн талбайг олох шаардлагатай
L=((x,y): x=a(t - sin t), y=a(1 - зардал), 0≤ t ≤ 2π)
Интеграл тооцоонд параметрийн дагуу сегмент дээр өгөгдсөн муруйн х тэнхлэгийг тойрсон эргэлтийн биеийн гадаргуугийн талбайг олох дараах томъёо байдаг: x=φ(t), y=ψ(t) (t) 0 ≤t ≤t 1)
Энэ томъёог манай циклоид тэгшитгэлд ашигласнаар бид дараахь зүйлийг олж авна.

Даалгаврын дугаар 4. Циклоид нумыг эргүүлснээр олж авсан биеийн эзэлхүүнийг ол
![]()
Үхрийн тэнхлэгийн дагуу.
Интеграл тооцоололд эзлэхүүнийг судлахдаа дараахь зүйлийг тэмдэглэнэ.
Хэрэв муруйн трапецийг хязгаарлах муруй нь параметрийн тэгшитгэлээр өгөгдсөн бөгөөд эдгээр тэгшитгэлийн функцууд нь тодорхой интеграл дахь хувьсагчийн өөрчлөлтийн тухай теоремын нөхцөлийг хангаж байвал Окс тэнхлэгийг тойрон трапецын эргэлтийн биеийн эзэлхүүн . томъёогоор тооцоолно

Энэ томьёог ашиглан өөрт хэрэгтэй эзлэхүүнээ олъё.
Асуудал шийдэгдэж.
Дүгнэлт
Тиймээс энэ ажлын явцад циклоидын үндсэн шинж чанаруудыг тодруулсан. Тэд мөн циклоидыг хэрхэн бүтээхийг сурч, циклоидын геометрийн утгыг олж мэдсэн. Циклоид нь зөвхөн математикт төдийгүй технологийн тооцоолол, физикт асар их практик хэрэглээтэй болсон. Гэхдээ циклоид нь бусад давуу талуудтай. Үүнийг 17-р зууны эрдэмтэд муруй шугамыг судлах аргуудыг боловсруулахад ашигласан бөгөөд эцэст нь дифференциал ба интеграл тооцоог зохион бүтээхэд хүргэсэн аргууд юм. Энэ нь мөн Ньютон, Лейбниц болон тэдний анхны судлаачид математикийн шинэ хүчирхэг аргын хүчийг туршиж үзсэн "хүрч чулууны" нэг байв. Эцэст нь брахистохроны асуудал нь өнөөгийн физикчдэд зайлшгүй шаардлагатай өөрчлөлтийн тооцоог зохион бүтээхэд хүргэсэн. Ийнхүү циклоид нь математикийн түүхэн дэх хамгийн сонирхолтой үеүүдийн нэгтэй салшгүй холбоотой байв.
Уран зохиол
1. Берман Г.Н. Циклоид. - М., 1980
2. Веров С.Г. Брахистохрон эсвэл циклоидын өөр нэг нууц // Квант. - 1975. - No5
3. Веров С.Г. Циклоид нууцууд// Квант. - 1975. - No8.
4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С., Радченко Т.Н. Тодорхой интегралын хэрэглээ. Физикийн факультетийн 1-р курсын оюутнуудад зориулсан заавар, бие даасан даалгавар. - Ростов n / a: UPL RSU, 1994.
5. Гиндикин С.Г. Циклоид одны эрин үе // Квант. - 1985. - No6.
6. Фихтэнголц Г.М. Дифференциал ба интеграл тооцооллын курс. T.1. - М., 1969
Ийм мөрийг "дугтуй" гэж нэрлэдэг. Муруй шугам бүр нь шүргэгчийн дугтуй юм.
Матери ба хөдөлгөөн, тэдгээрийн бүрдүүлдэг арга нь үнэний мэдлэг дэх өөрийн чадавхийг хэрэгжүүлэх боломжийг хүн бүрт олгодог. Диалектик-материалист сэтгэлгээний хэлбэрийг хөгжүүлэх арга зүйг боловсруулах, танин мэдэхүйн ижил төстэй аргыг эзэмших нь хүний хөгжлийн асуудлыг шийдвэрлэх, хүний боломжуудыг хэрэгжүүлэх хоёр дахь алхам юм. XX боломжуудын фрагмент...
Нөхцөл байдал нь неврастения - неврозоор өвдөж болзошгүй бөгөөд клиник зураглалын үндэс нь астеник өвчин юм. Неврастения болон мэдрэлийн эмгэгийн декомпенсацийн үед оюун санааны (сэтгэл зүйн) хамгаалалтын мөн чанар нь ургамлын эмгэг бүхий цочромтгой сул дорой байдал, хүндрэлээс ангижрах замаар илэрдэг: эсвэл хүн өөрийн мэдэлгүй дайралтаас илүүтэйгээр "тулалддаг". ...





Төрөл бүрийн үйл ажиллагаа; сургуулийн сурагчдын орон зайн төсөөлөл, орон зайн дүрслэл, дүрслэл, орон зайн, логик, хийсвэр сэтгэлгээг хөгжүүлэх; янз бүрийн хэрэглээний асуудлыг шийдвэрлэхэд геометрийн болон график мэдлэг, ур чадварыг ашиглах ур чадварыг бий болгох; техникийн болон ... чиглэлээр төслийн үйл ажиллагааны үе шатуудын агуулга, дараалалтай танилцах.
Нуманууд. Спираль нь мөн тойргийн эволют гэх мэт хаалттай муруйн эволютууд юм. Зарим спиральуудын нэрийг тэдгээрийн туйлын тэгшитгэл нь декартын координат дахь муруйн тэгшитгэлүүдтэй ижил төстэй байдлаар өгдөг, жишээлбэл: параболик спираль (a - r)2 = bj, гипербол спираль: r = a/j. Саваа: r2 = a/j si-ci-спираль, параметрийн тэгшитгэл нь дараах байдалтай байна: , )