Enviar seu bom trabalho na base de conhecimento é simples. Use o formulário abaixo
Estudantes, estudantes de pós-graduação, jovens cientistas que usam a base de conhecimento em seus estudos e trabalhos ficarão muito gratos a você.
postado em http://www.allbest.ru/
instituição educacional
"Estado Pedagógico da Bielorrússia
Universidade Maxim Tank
Faculdade de Física e Matemática
Departamento de Matemática e Métodos de Ensino de Matemática
TRABALHO DO CURSO SOBRE O ASSUNTO
"CICLÓIDE"
Minsk, 2016
arco ciclóide pêndulo tautócrono
- Introdução
- 1. Propriedades básicas da ciclóide
- 2. Definição geométrica de uma ciclóide
- 3. Área do arco da ciclóide
- 4. Comprimento do arco do arco ciclóide
- 5. O volume do corpo obtido pela rotação do arco da ciclóide
- 6. O melhor pêndulo
- Conclusão
- Bibliografia
INTRODUÇÃO
O tema do meu trabalho de curso é a ciclóide. Esta curva é notável de muitas maneiras. É também o traço do ponto do aro da roda rolante, é também a curva de oscilações de período constante, é também a curva da descida mais rápida. Atualmente, as curvas cicloidais são utilizadas em muitos cálculos técnicos, e o conhecimento dessas curvas facilita o estudo de peças de máquinas. Sem entrar em detalhes, mencionamos que as propriedades das curvas cicloidais são utilizadas na construção de perfis de dentes de engrenagens e em muitas outras questões técnicas. Mesmo do ponto de vista puramente aplicado, essas curvas merecem a atenção mais séria. Portanto, considerei este tema relevante e interessante para estudar.
Que problemas surgem no estudo da ciclóide? Em primeiro lugar, é necessário dar-lhe uma definição puramente geométrica, independente da mecânica. Em seguida, você precisa estudar suas propriedades, considerar a tangente, calcular a área limitada pelo arco da ciclóide e sua base, o comprimento do arco, o volume do corpo formado pela rotação do arco da ciclóide em torno do linha guia.
O trabalho do curso considerará detalhadamente a propriedade tautócrona da ciclóide e sua aplicação para criar o melhor pêndulo. A importância dos relógios de pêndulo não pode ser subestimada, pois até recentemente eles serviam como os relógios mais precisos que garantiam o serviço do tempo nos observatórios astronômicos.
Outro mérito da ciclóide, que deve ser observado, é que ela foi usada por cientistas no desenvolvimento de técnicas para estudar linhas curvas, o que levou à invenção do cálculo diferencial e integral. Em meu trabalho, proponho comparar o cálculo do comprimento do arco do arco ciclóide, a área da superfície sob o arco e os volumes de corpos formados pela rotação do arco ciclóide antes do advento do cálculo integral, longos e não sempre absolutamente estrito, e usando integração.
Objetivo: estudo de material sobre o tema "Cicloide"; estudo das características do melhor pêndulo; comparação do estudo de linhas curvas antes e depois do aparecimento do cálculo integral, cálculo do comprimento do arco do arco ciclóide, a área de superfície sob o arco e os volumes dos corpos formados pela rotação do arco ciclóide.
1. PRINCIPAIS PROPRIEDADES DA CICLODIA
Primeiro você precisa descobrir que tipo de curva é chamada de ciclóide.
Considere um círculo de raio uma centrado no ponto A. Deixe o círculo em questão rolar sem deslizar ao longo do eixo OX. Uma curva descrita por qualquer ponto do círculo é chamada ciclóide.
Essa definição da ciclóide nunca satisfez os cientistas: afinal, ela se baseia em conceitos mecânicos - velocidades, acréscimos de movimentos, etc. tal definição, você deve primeiro estudar as propriedades básicas da ciclóide, usando sua definição mecânica. Ao escolher a mais simples e característica dessas propriedades, podemos usá-la como base de uma definição geométrica.
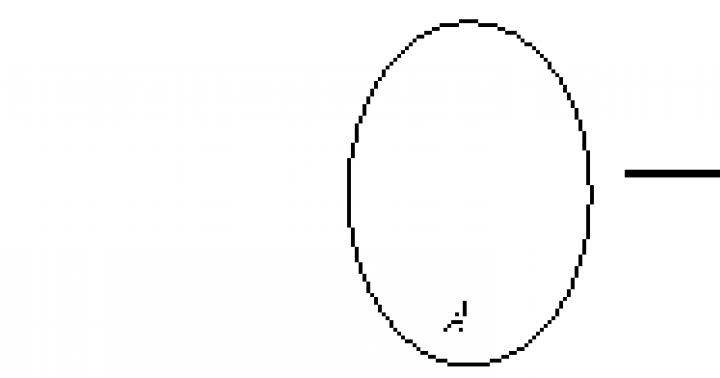
Vamos começar estudando a tangente e a normal à ciclóide. o que tangente para uma linha torta, todos imaginam com bastante clareza; portanto, não a apresentaremos aqui. normal chamada perpendicular à tangente, restaurada no ponto de contato. Na fig. 1.1 mostra a tangente e a normal à curva AB em seu ponto M.
Considere uma ciclóide (Fig. 1.2). O círculo rola em uma linha reta AB. Suponhamos que o raio vertical do círculo, que no momento inicial passava pelo ponto mais baixo da ciclóide, conseguiu girar um ângulo χ e assumiu a posição OM. Em outras palavras, acreditamos que o segmento M o T é uma fração do segmento M o M 1 que o ângulo q é de uma volta completa. Neste caso, o ponto M 0 chegou ao ponto M.
O ponto M é o ponto da ciclóide que nos interessa.
Flecha Oh representa a velocidade do centro do círculo rolante. Todos os pontos do círculo, incluindo o ponto M, têm a mesma velocidade horizontal, mas, além disso, o ponto M participa da rotação do círculo. A velocidade MC, que o ponto M do círculo recebe durante esta rotação, é dirigida tangencialmente EM 1 ao círculo, ou seja, perpendicular ao raio OM. E desde neste caso, a velocidade MS é igual em magnitude à velocidade MP (ou seja, a velocidade ELE). Portanto, o paralelogramo de velocidades no caso de nosso movimento será um losango (o losango do MSKR na Fig. 1.2). A diagonal MK deste losango nos dará apenas uma tangente à ciclóide.
Tudo isso permite resolver o seguinte problema de construção: dada a linha diretora AB da ciclóide, o raio r do círculo gerador e o ponto M pertencente à ciclóide (Fig. 1.2). É necessário construir uma tangente do MK à ciclóide.
Tendo um ponto M, podemos facilmente construir um círculo gerador, em sua posição quando o ponto do círculo cai em M. Para fazer isso, primeiro encontramos o centro O usando um raio MO= r (o ponto O deve estar em uma linha reta paralela a AB, a uma distância r dele). Em seguida, construímos um segmento MP de comprimento arbitrário, paralelo à linha guia. Em seguida, construímos uma linha EM 1 , perpendicular a OM. Nesta linha, nos despedimos do ponto M segmento MC igual a MP. No MS e MP, como nas laterais, construímos um losango. A diagonal deste losango será a tangente à ciclóide no ponto M.
Esta construção é puramente geométrica, embora a tenhamos obtido usando os conceitos da mecânica. Agora podemos dizer adeus à mecânica e obter mais consequências sem a ajuda dela. Vamos começar com um teorema simples.
Teorema 1. Ângulo entre tangente a cicloide (em um ponto arbitrário) e a linha diretora é igual ao complemento de 90° metade do ângulo de rotação do raio do círculo gerador.
Em outras palavras, na fig. 1.2
? KLT igual ou
Vamos agora provar esta igualdade. Para encurtar a fala, concordaremos em chamar o ângulo φ de rotação do raio do círculo gerador de "ângulo básico". Isso significa que o ângulo MOT na Fig. 1.2 - o ângulo principal. Vamos supor que o ângulo principal é agudo. Para o caso em que o círculo de rolamento faz mais de um quarto de volta completa, a prova será semelhante.
Considere o ângulo CMP. O lado CM é perpendicular OM(a tangente ao círculo é perpendicular ao raio). Lado MP (horizontal) perpendicular a A PARTIR DE(em direção à vertical). Mas o ângulo MOP, pela condição, é agudo, e o ângulo CMP é obtuso. Então os cantos OIT e SMR somam 180° (ângulos com lados mutuamente perpendiculares, sendo um agudo e o outro obtuso).
Assim, o ângulo CMP é igual a 180° -ts. Mas, como você sabe, a diagonal de um losango corta o ângulo no vértice. Por isso, Hugo
KMR = 90° -,
Q.E.D.
Vamos agora voltar nossa atenção para a normal à ciclóide. Vamos representar o lado esquerdo da Fig. 1.2 é maior, e vamos desenhar um normal EU (EU ? MK; arroz. 1.3).
Da fig. 1.3 segue que o ângulo EMP é igual à diferença dos ângulos KME e KMR, ou seja é igual a 90° - ? KMP.
Mas acabamos de provar que a própria esquina KMRé igual a 90° -
Assim, obtemos:
? ERM= 90° - ? KMR= 90° - (90° -) =
Provamos um teorema simples, mas útil. Vamos formular:
Teorema 2.Ângulo entre a normal à ciclóide (em qualquer ponto dele) e a linha guia é igual à metade do "ângulo principal".
Vamos conectar o "ponto (T) do círculo gerador agora com o ponto M" (o ponto "atual" da ciclóide) com o "inferior" (com o ponto de contato do círculo gerador e a linha de direção - Fig. 1.3). O triângulo MOT é obviamente isósceles (OM e A PARTIR DE são os raios do círculo gerador). A soma dos ângulos da base desse triângulo é igual a 180 ° - u, e cada um dos ângulos da base é um tapete dessa soma. Então, ? OMT= 90° - .
Preste atenção no canto RMT.É igual à diferença de ângulo HTA e OMR. Já vimos que ? OMT igual a 90° - ; quanto ao ângulo OMP, não é difícil descobrir a que é igual. Afinal, o canto OMR igual ao ângulo DOM(ângulos internos cruzados quando paralelos).
É imediatamente óbvio que ? DOM igual a 90 ° - c. Significa, ? OMP= = 90° - c. Assim, obtemos:
RMT = ? HTA - ? OMR \u003d 90 ° - - (90 ° - c) \u003d.
Acontece um resultado maravilhoso: o ângulo RMT acaba por ser igual ao ângulo PME (pelo Teorema 2). Portanto, o ME direto e o MT se fundirão! Nosso arroz. 1.3 não é bem feito! O arranjo correto de linhas é dado na fig. 1.4.
Vamos formular o resultado obtido na forma do Teorema 3.
Teorema 3 (a primeira propriedade principal da ciclóide). A normal à ciclóide passa pelo ponto "inferior" do círculo gerador.
Este teorema tem um corolário simples. O ângulo entre uma tangente e uma normal é, por definição, um ângulo reto. Este é o ângulo inscrito na circunferência do círculo gerador. Portanto, deve ser baseado no diâmetro do círculo. Então, TT 1 -- diâmetro e T 1 -- ponto "superior" do círculo gerador. Vamos formular o resultado obtido.
Consequência (a segunda propriedade principal da ciclóide). A tangente à ciclóide passa pelo ponto "superior" do círculo gerador.
Para explicar essa propriedade, precisamos construir uma ciclóide.
A construção da ciclóide é realizada na seguinte sequência:
1. Na linha guia horizontal, é colocado um segmento AA 12, igual ao comprimento do círculo gerador de raio r, (2pr);
2. Construir um círculo gerador de raio r, de modo que a linha diretora seja tangente a ele no ponto A;
3. O círculo e o segmento AA 12 são divididos em várias partes iguais, por exemplo 12;
4. A partir dos pontos de divisão 1 1 , 2 1 , ...12 1 restaure as perpendiculares à interseção com a continuação do eixo horizontal do círculo nos pontos 0 1 , 0 2 , ...0 12 ;
5. A partir dos pontos de divisão do círculo 1, 2, ... 12, são traçadas linhas retas horizontais, nas quais são feitas serifas com arcos de um círculo de raio r;
6. Os pontos obtidos A 1 , A 2 , ... A 12 pertencem à ciclóide.
Na fig. 1.6 a base da ciclóide é dividida em 6 partes iguais;
Quanto maior o número de divisões, mais preciso será o desenho. Em cada ponto da ciclóide construída por nós, traçamos uma tangente, ligando o ponto da curva com o ponto "superior" do círculo gerador. Em nosso desenho, temos sete tangentes (duas delas são verticais). Agora, desenhando a ciclóide à mão, cuidaremos para que ela realmente toque cada uma dessas tangentes: isso aumentará significativamente a precisão do desenho. Neste caso, a própria ciclóide irá contornar todas essas tangentes).
Vamos executar no mesmo figo. 1,6 normais em todos os pontos encontrados da ciclóide. No total serão cinco normais, sem contar o guia. É possível construir manualmente o envelope dessas normais. Se, em vez de seis, tivéssemos 12 ou 16 pontos de divisão, haveria mais normais no desenho e o envelope seria delineado com mais clareza. Tal envelope de todas as normais desempenha um papel importante no estudo das propriedades de qualquer linha curva. No caso de uma ciclóide, um fato curioso é revelado: a envoltória das normais da ciclóide é exatamente a mesma ciclóide, apenas deslocada em 2 uma para baixo e para baixo ra Para a direita. Este fato é característico da ciclóide.
2. DEFINIÇÃO GEOMÉTRICA DE UMA CICLODIA
Agora damos uma definição da ciclóide como o lugar geométrico dos pontos sem usar a mecânica. É mais fácil fazê-lo. Considere uma linha arbitrária AB(consideraremos condicionalmente sua direção como horizontal) e um ponto sobre ela M 0 . Em seguida, considere todos os círculos possíveis de um determinado raio que são tangentes a essa linha e localizados em um lado dela. Em cada círculo do ponto T tocando-o com uma linha reta AB posto de lado (na direção do ponto M 0 ) arco tm, igual em comprimento ao segmento M 0 T. Lugar de pontos M(tomado em todos os círculos que mencionamos) e será uma ciclóide.
Vamos estabelecer mais uma propriedade importante da ciclóide e tentar usá-la como base para o estudo desta curva.
Considere um triângulo MTT 1 (Fig. 2.1), formado pelo diâmetro vertical do círculo gerador, a tangente à ciclóide e a normal a ela.
Canto MT 1 T, como inscrito em um círculo, é igual à metade do ângulo central baseado no mesmo arco, ou seja, igual a. Vamos gastar MK||AB e EU?AB. O segmento ME desempenhará um papel significativo no futuro, por isso daremos um nome e uma designação: chamaremos de “altura” do ponto M da ciclóide e o denotaremos pela letra h. Então a altura do ponto M as ciclóides são sua distância da linha de direção.
Vamos prestar atenção ao ângulo KMT. É igual ao ângulo MT 1 T. De um triângulo TMT 1 Nós temos:
MT = 2 umapecado e do triângulo TKM:
CT = MT sen.
Comparando esses resultados e notando que CT = h, finalmente temos:
h = 2 uma pecado 2.
Expressamos a altura do ponto M em termos do ângulo entre a tangente no ponto M e a vertical (ainda consideramos a direção da reta AB como horizontal). Agora vamos expressar o seno desse ângulo em termos de "altura". Obtemos, obviamente:
por onde k a constante de valor para a ciclóide dada é denotada . Apresentamos o resultado obtido no teorema.
Teorema 4. O seno do ângulo entre a tangente à ciclóide no ponto M e a vertical é proporcional à raiz quadrada da “altura” do ponto M.
Obviamente, qualquer ciclóide possui esta propriedade. Surge a pergunta: em que medida essa propriedade caracteriza exatamente a ciclóide: qualquer curva que possua essa propriedade será necessariamente uma ciclóide? Pode-se provar que este será o caso, -- que o seguinte teorema (inverso) também é verdadeiro:
Teorema 5. Dada uma linha AB e um ponto M, então a única curva que satisfaz as condições do Teorema 4 e passa pelo ponto M é uma ciclóide.
Além disso, o raio do círculo gerador desta ciclóide está relacionado com o coeficiente k, que é mencionado no Teorema 4, pela seguinte relação:.
Também vale a pena atentar para outra curva notável, que se chama companheiro da ciclóide.
Considere uma ciclóide (Figura 2.2). A partir de seu ponto M, abaixamos a perpendicular ao diâmetro vertical do círculo gerador. Vamos pegar o ponto P. Vamos fazer essa construção para todos os pontos da ciclóide sem exceção.
Então o ponto P descreverá alguma curva. Essa curva é chamada de companheira da ciclóide.
Considere uma ciclóide, um ponto M nela e o ponto correspondente P no satélite (Fig. 2.3). O centro do círculo gerador será denotado pela letra Q. Então teremos:
QP=QM cos?MQP= uma cos(180 0 -ts)=- uma cos=- uma sin(90 0 -ts)= uma sin(c -90 0).
Tracemos o lugar geométrico dos centros do círculo gerador (linha reta XX 1 ). do ponto M 0 adiado por AB segmento de linha M 0 K, igual. Vamos gastar KY ? XX 1 . O ponto de intersecção destas linhas será indicado pela letra O. Segmento de linha M 0 R na linha reta que vai da ponta da ciclóide até o ponto de contato do círculo gerador é igual a uma c, onde c é o ângulo principal MQR, expressa em radianos. Segmento de linha OQ no eixo horizontal XX 1 é igual a M 0 R - M 0 K=uma(c -), e o segmento QPé igual a uma pecado? PMQ, ou seja, igual ao seno do ângulo (c -), multiplicado pelo raio uma.
Então do ponto O horizontalmente, são traçados segmentos iguais em comprimento aos arcos de um círculo e ao longo das linhas verticais dos senos dos ângulos correspondentes a esses arcos. Esta é a construção de uma sinusóide comum conhecida por nós.
Significa, O companheiro de uma ciclóide é chamado de senóide.
Não nos aprofundaremos no estudo das propriedades dessa curva verdadeiramente notável, apenas observaremos como fato a área delimitada pelo companheiro de um arco da ciclóide e sua base é igual ao dobro da área do círculo gerador.
3. PRAÇA DO ARCO DA CICLODIA
A primeira menção ao cálculo da área delimitada entre o arco da ciclóide e sua base está nos trabalhos de Viviani e Torricelli. Ao mesmo tempo, eles usaram uma técnica especial, que foi chamada de "método dos indivisíveis". Este método consiste no fato de que uma figura curvilínea é dividida em tiras infinitamente finas, cuja área é relativamente fácil de encontrar e, em seguida, essas áreas são somadas. Essa técnica levou ao surgimento do cálculo integral meio século depois.
Considere uma figura limitada por um arco ciclóide e uma senóide. Na figura 3.1, esta figura, composta por duas pétalas, é circulada com uma linha grossa. Vamos calcular sua área.
Em primeiro lugar, vamos construir uma imagem espelhada da pétala direita da figura em relação à linha reta AB (essa reflexão é dada na Figura 4.1 por uma linha tracejada). Vamos então mover essa curva tracejada para cima para a esquerda e aplicá-la à pétala esquerda de modo que os arcos das senóides incluídas no contorno de cada uma das pétalas coincidam. Obtemos uma figura convexa, sombreada na figura 3.1 e representada separadamente na fig. 3.2. Essa figura é chamada a figura de Roberval. Vamos estabelecer as propriedades mais importantes desta figura.
1. A figura convexa M 0 RLM é igual em tamanho à figura de duas pétalas representada pela linha grossa na Fig. 3.1. Isso pode ser visto pelo fato de ser "composto" pelas mesmas pétalas.
2. Qualquer corda horizontal de uma figura convexa é igual a duas vezes a corda de uma pétala à mesma distância de AB. De fato, as cordas CE e PH (Fig. 3.1) da pétala direita, equidistantes do círculo gerador, estão igualmente distantes do centro. Então CT \u003d CE \u003d PH \u003d P 1 H 1 \u003d TL.
Isso dá um resultado importante: a corda MR de uma figura convexa (Fig. 3.2) é igual à corda do círculo gerador SK, localizado à mesma distância da linha diretora.
Consideremos agora a figura convexa de Roberval e o círculo tangente às mesmas linhas AB e A 1 B 1, e conecte os pontos de sua interseção com o círculo e com o contorno da figura convexa sucessivamente por segmentos de reta, como mostrado na figura. Os polígonos inscritos assim obtidos (HLMNPQRSTK e H 1 L 1 M 1 N 1 P 1 Q 1 R 1 S 1 T 1 K 1) serão chamados de polígonos "correspondentes" em uma série de trapézios (e triângulos). As áreas dos trapézios “correspondentes” no círculo e na figura de Robervel, por exemplo, NPRS e N 1 P 1 R 1 S 1, são iguais, pois esses trapézios, respectivamente, possuem as mesmas bases inferiores, bases superiores (correspondentes acordes) e alturas. Na fig. 3.2 trapézios correspondentes de tamanho igual são cobertos com a mesma hachura.
Vamos agora aumentar indefinidamente o número de linhas retas "intermediárias" paralelas a AB, de modo que a distância entre qualquer par vizinho tenda a zero. Então, em um círculo, obtemos uma série de polígonos inscritos, cujo número de lados aumenta indefinidamente, e cada um dos lados tende a zero. Sabemos que as áreas S n desses polígonos são limitadas pela área de um círculo:
limite S n=p uma 2 .
Como se comportará a sequência de polígonos inscritos em uma figura convexa de Roberval nesse caso? Quadrado? n polígonos inscritos consecutivos tenderão a área? figuras de Roberval. Sabe-se que se duas variáveis retêm valores correspondentemente iguais para todas as suas mudanças e uma delas tende a um certo limite, a outra tende ao mesmo limite. Mas cada polígono inscrito na figura de Roberval é igual em tamanho ao polígono correspondente inscrito no círculo. Concluímos, portanto, que o limite das áreas dos polígonos inscritos em uma figura de Roberval é igual ao limite das áreas dos polígonos correspondentes inscritos em um círculo; o que significa que a área da figura convexa de Roberval é igual à área do círculo gerador:
Disso obtemos uma consequência imediata: a área da figura de duas pétalas é igual à área do círculo gerador.
Vejamos agora a Figura 3.1. A área da figura AOTPBKA, como vimos, é igual ao dobro da área do círculo gerador. Acabamos de determinar a área da figura de duas pétalas: é igual à área do círculo gerador. Consequentemente, a área limitada pelo arco da ciclóide e sua base é igual a três vezes a área do círculo gerador.
Agora vamos encontrar a área entre o arco da ciclóide e sua base usando geometria diferencial.
Onde t? .
Vamos encontrar a derivada
4. COMPRIMENTO DO ARCO DO CICLOIDE
O comprimento do arco de uma ciclóide foi calculado pela primeira vez pelo arquiteto e matemático inglês Wren em 1658. Wren partiu de considerações mecânicas que lembravam os primeiros trabalhos de Torricelli e Roberval. Ele considerou a rotação de um círculo rolante através de um ângulo muito pequeno perto do ponto "inferior" do círculo gerador. A fim de dar força probatória às considerações sugestivas de Wren, seria preciso considerar vários teoremas auxiliares e, portanto, teríamos que gastar muito trabalho.
É muito mais conveniente usar um caminho mais longo, mas mais suave. Para fazer isso, você precisa considerar uma curva especial que toda curva plana possui - sua varredura.
Considere um arco convexo AB de uma linha curva (Fig. 4.1). Imaginemos que um fio flexível e inextensível do mesmo comprimento que o próprio arco AB está preso ao arco AB no ponto A, e esse fio é “enrolado” na curva e o une firmemente, de modo que sua extremidade coincida com o ponto B .Vamos “desenrolar” - endireitar o fio, mantendo-o bem esticado, de forma que a parte livre do fio CM esteja sempre direcionada tangencialmente ao arco AB. Nestas condições, a extremidade da rosca descreverá alguma curva. É essa curva que é chamada de varredura, ou, em latim, involuir curva original.
Se o arco da curva não for em toda parte convexo em uma direção, se for, como a curva AB na Fig. 4.2 tem um ponto C no qual a tangente à curva passa de um lado para o outro (tal ponto é chamado de ponto de inflexão), então neste caso também podemos falar sobre o desenvolvimento da curva, mas o raciocínio terá ser um pouco mais complicado.
Imagine que o fio é fixado exatamente no ponto de inflexão C (Fig. 4.2). O fio, enrolando do arco BC, descreverá a curva BMP - uma varredura.
Agora imagine um fio enrolado em torno do arco AC da curva original, mas este fio já está alongado: no ponto C, um pedaço de fio CP está preso a ele. Ao enrolar um fio ACP alongado com uma curva SA, obtemos um arco de RNA que, junto com o arco BMP, forma uma única curva contínua - contínua, mas nem sempre suave: o ponto de deflexão C da curva original corresponderá à ponta (ponto de retorno) da curva VMRNA: a curva VMRNA será uma involuta (varredura) da curva ICA.
Esses exemplos nos ajudaram a nos acostumar com os novos conceitos de evoluir e evolutivo. Agora vamos estudar o desdobramento de curvas cicloidais.
Estudando esta ou aquela curva, muitas vezes construímos uma curva auxiliar - uma "companheira" dessa curva. Então, custamos uma sinusóide - uma companheira de uma ciclóide. Agora, a partir da ciclóide dada, construímos uma ciclóide auxiliar inextricavelmente ligada a ela. Acontece que o estudo conjunto de tal par de ciclóides é, em alguns aspectos, mais fácil do que o estudo de uma única ciclóide. Chamaremos tal ciclóide auxiliar de ciclóide acompanhante.
Considere metade do arco da ciclóide AMB (Fig. 4.3). Não devemos nos envergonhar de que essa ciclóide esteja localizada de maneira incomum (“de cabeça para baixo”). Vamos desenhar 4 linhas paralelas à linha de direção AK nas distâncias uma, 2uma, 3uma e 4 uma. Vamos construir um círculo gerador na posição correspondente ao ponto M (na Fig. 4.3, o centro deste círculo é indicado pela letra O). O ângulo de rotação de MON será denotado por c. Então o segmento AN será igual a bc (o ângulo u é expresso em radianos).
Continuamos o diâmetro HT do círculo gerador além do ponto T até ele cruzar (no ponto E) com a reta PP. Em TE como diâmetro, construímos um círculo (com centro O 1). Vamos construir uma tangente no ponto M à ciclóide AMB. Para fazer isso, o ponto M deve, como sabemos, estar conectado ao ponto T. Continuamos a tangente MT além do ponto T até a interseção com o círculo auxiliar e chamaremos o ponto de interseção M 1. É deste ponto M 1 que agora queremos tratar.
Denotamos o ângulo MON por c. Portanto, o ângulo MTH será igual a (ângulo inscrito com base no mesmo arco). Triângulo TO 1 M 1, obviamente, isósceles. Portanto, não apenas o ângulo O 1 TM 1, mas também o ângulo TM 1 O 1 serão iguais. Assim, a parte do ângulo TO 1 M 1 no triângulo TO 1 M 1 permanece exatamente p - q radianos (lembre-se de que o ângulo 180? é igual a p radianos). Notamos também que o segmento NK é obviamente igual a b (p - c).
Considere agora um círculo com centro O 2, mostrado na Figura 4.3 por uma linha tracejada. A partir do desenho fica claro que tipo de círculo é. Se você rolar sem deslizar ao longo da linha reta CB, seu ponto B descreverá a ciclóide BB. Quando o círculo tracejado gira pelo ângulo p - c, o centro O 2 chegará ao ponto O 1 e o raio O 2 B tomará a posição O 1 M 1. Assim, o ponto M 1 construído por nós acaba por ser um ponto da ciclóide BB.
A construção descrita atribui a cada ponto M da ciclóide AMB um ponto M 1 da ciclóide VM 1 B. Na fig. 4.4 esta correspondência é mostrada com mais clareza. A ciclóide obtida dessa maneira é chamada de ciclóide acompanhante. Na fig. 4.3 e 4.4, as ciclóides representadas por linhas tracejadas em negrito são acompanhadas em relação às ciclóides representadas por linhas sólidas em negrito.
Da fig. 4.3 pode-se ver que a linha MM 1 é a normal no ponto M 1 à ciclóide que a acompanha. De fato, essa linha passa pelo ponto M 1 da ciclóide e pelo ponto T de tangência entre o círculo gerador e a linha diretora (o ponto "mais baixo" do círculo gerador, como costumávamos dizer; agora acabou sendo ser o "mais alto", porque o desenho é girado). Mas esta mesma linha, por construção, é tangente à “base” da ciclóide AMB. Assim, a ciclóide original toca todas as normais da ciclóide que a acompanha. É o envelope para as normais da ciclóide acompanhante, ou seja, a evolução dela. E a ciclóide "acompanhante" acaba por ser simplesmente uma involuta da ciclóide original!
Trabalhando nessa construção complicada, mas essencialmente simples, provamos um teorema notável descoberto pelo cientista holandês Huygens. Aqui está o teorema: a evoluta de uma ciclóide é exatamente a mesma ciclóide, apenas deslocada.
Tendo construído uma evoluta não para um arco, mas para toda a ciclóide (o que, é claro, só pode ser feito mentalmente), então uma evoluta para esta evoluta, etc., obtemos a Fig. 4.5, assemelhando-se a telhas.
Prestemos atenção ao fato de que, ao provar o teorema de Huygens, não usamos estimativas infinitesimais, indivisíveis ou aproximadas. Nem mesmo usávamos mecânica, embora às vezes usássemos expressões emprestadas da mecânica. Esta prova está inteiramente no espírito do raciocínio usado pelos cientistas do século XVII quando queriam fundamentar rigorosamente os resultados obtidos com a ajuda de várias considerações sugestivas.
Um corolário importante segue imediatamente do teorema de Huygens. Considere o segmento AB da Fig. 4.4. O comprimento deste segmento é obviamente igual a 4 uma. Imagine agora que um fio é enrolado no arco da ciclóide AMB, fixado no ponto A e equipado com um lápis no ponto B. Se “enrolarmos” o fio, o lápis se moverá ao longo do desenvolvimento da ciclóide AMB, ou seja, ao longo da ciclóide BM 1 B. O comprimento do fio, igual ao comprimento do semi-arco da ciclóide, obviamente será igual ao segmento AB, ou seja, como vimos, 4 uma. Portanto, o comprimento L de todo o arco da ciclóide será igual a 8 uma, e fórmula L=8 uma pode agora ser considerado suficientemente rigorosamente comprovado.
Calculamos o comprimento do arco usando geometria diferencial. A solução obtida dessa maneira será muito mais curta e fácil:
Onde t?
r(t)=
=
| r(t)|===2sen
5. VOLUME DO CORPO OBTIDOS PELA ROTAÇÃO DO ARCO DO CICLOIDE
Vamos encontrar o volume do corpo gerado pela rotação do arco ciclóide em torno de sua base. Roberval o encontrou quebrando o corpo em forma de ovo resultante (Fig. 5.1) em camadas infinitamente finas, inscrevendo cilindros nessas camadas e somando seus volumes. A prova é longa, tediosa e não inteiramente rigorosa. Portanto, para calculá-lo, nos voltamos para a matemática superior. Vamos definir a equação ciclóide parametricamente.
No cálculo integral, ao estudar volumes, ele usa a seguinte observação:
Se a curva que limita o trapézio curvilíneo é dada por equações paramétricas e as funções nestas equações satisfazem as condições do teorema sobre a mudança de variável em uma certa integral, então o volume do corpo de rotação do trapézio em torno do eixo Ox será ser calculado pela fórmula:
Vamos usar esta fórmula para encontrar o volume que precisamos.
Da mesma forma, calculamos a superfície desse corpo.
L=((x,y): x=a(t - sin t), y=a(1 - custo), 0 ? t ? 2р)
No cálculo integral, existe a seguinte fórmula para encontrar a área da superfície de um corpo de revolução em torno do eixo x de uma curva especificada em um segmento parametricamente (t 0 ?t ?t 1):
Aplicando esta fórmula à nossa equação ciclóide, obtemos:
Considere também outra superfície gerada pela rotação do arco ciclóide. Para fazer isso, construiremos um reflexo espelhado do arco ciclóide em relação à sua base e giraremos a figura oval formada pela ciclóide e sua reflexão em torno do eixo KT (Fig. 5.2)
Primeiro, vamos encontrar o volume do corpo formado pela rotação do arco ciclóide em torno do eixo KT. Seu volume será calculado pela fórmula (*):
Assim, calculamos o volume de metade desse corpo de nabo. Então o volume total será
Para encontrar a área da superfície desse corpo de revolução usando a integral, também é necessário dividi-lo ao meio horizontalmente e considerar sua parte superior.
Assim, a área da superfície do corpo resultante é
6. O MELHOR PÊNDULO
Observando o candelabro balançando no templo, Galileu descobriu que o tempo do balanço completo do candelabro, ou seja, o tempo após o qual ele retornará à sua posição original (o chamado período de oscilação), foi o mesmo para grandes e pequenos vãos. Essa observação levou Galileu a pensar que um corpo oscilante (um pêndulo) poderia ser usado para controlar o funcionamento de um relógio.
O próprio Galileu não conseguiu fazer um relógio com pêndulo, e logo ficou claro que suas observações eram imprecisas. Observações mais precisas mostraram que o período de oscilação do pêndulo é tanto maior quanto maior a oscilação; mas devido ao inevitável atrito do eixo e da resistência do ar, a oscilação de um pêndulo comum diminui constantemente, o que significa que seu período de oscilação também diminuirá. Relógio com um pêndulo comum - também chamado pêndulo circular(porque cada ponto descreve um arco de um círculo) não pode ir corretamente.
Huygens descobriu como fazer um pêndulo circular para que ele tenha uma oscilação constante. Mas ele também resolveu outro problema interessante - ele respondeu à pergunta de qual curva o ponto deve se mover para que o período de suas oscilações não dependa da amplitude. Ele criou um projeto que movia o centro de gravidade do pêndulo ao longo dessa curva.
Vamos começar com um dispositivo que garante o movimento correto de um relógio com um pêndulo circular. Engrenagem MAS(Fig. 6.1) ser acionado por uma corrente com um peso NO no final. Uma engrenagem é montada no eixo desta roda, firmemente conectada a ela. Essa engrenagem aciona os ponteiros do relógio e, portanto, é necessário que a roda MAS movido uniformemente.
Mas o peso NO, como qualquer corpo, sob a influência da gravidade se moverá de forma acelerada, conferindo rotação acelerada à roda MAS. O pêndulo deve eliminar a dificuldade MILÍMETROS.
Âncora A PARTIR DE deitado no plano da roda MAS, firmemente conectado ao pêndulo MM, MM pêndulo em si fica atrás do plano do desenho e, portanto, é desenhado com uma linha pontilhada. Âncora equipada com dentes H e Para.
No momento mostrado na Fig. roda 6.1 MAS segurado pelo pino esquerdo Hâncoras A PARTIR DE. Quando o pêndulo oscila para a esquerda, o pino H a âncora soltará a engrenagem capturada da roda, e a roda girará, mas apenas pelo rastreador, porque a engrenagem Paraâncoras cairão no espaço entre os dentes da roda e o atrasarão. Quando o pêndulo balança para a direita novamente, o pino desse lado será retido pela âncora. Assim, a cada giro completo do pêndulo (para frente e para trás), a roda girará exatamente um dente, ou seja, a uma certa fração do círculo. O movimento da roda será estritamente uniforme. Dentes de ancoragem, como visto na Fig. 6.1 são cortados obliquamente, de modo que o dente da roda, que foi retido pela âncora e solto novamente, deve deslizar na superfície oblíqua do dente da armadura. Como resultado, a âncora dará ao pêndulo um pequeno empurrão. Esses empurrões rítmicos compensarão a perda de energia que o pêndulo gasta para superar o atrito e a resistência do ar. Portanto, a oscilação do pêndulo não diminuirá. Assim, o peso transmite energia às duas rodas do relógio e ao próprio pêndulo, enquanto o pêndulo regula o curso do relógio.
E se o relógio parar? Não é difícil usá-los: basta levantar o peso e balançar o pêndulo. Mas, ao mesmo tempo, o balanço do balanço pode ser diferente, e o relógio andará uniformemente, mas incorretamente (vai adiantar ou começar a ficar para trás). A Huygens criou um dispositivo que permite ajustar facilmente o curso do relógio. Mas Huygens, como um verdadeiro cientista, estava interessado na questão: o que deveria ser um pêndulo "perfeito", um pêndulo cujo tempo de oscilação não depende da magnitude da oscilação? Vamos considerar em detalhes como a Huygens resolveu esse problema.
A palavra "tautocrona" significa "uniforme". Foi assim que Huygens chamou a curva, que ele começou a procurar, ou seja, tal curva ao longo da qual o centro de gravidade do pêndulo deve se mover de modo que o período de sua oscilação não dependa da magnitude da oscilação. A busca foi coroada de sucesso: a misteriosa tautócrona acabou por ser uma ciclóide pouco estudada. Ao fazê-lo, Huygens mostrou uma inteligência excepcional. Basta dizer que a doutrina dos evolutos foi criada no processo de resolver precisamente esse problema.
Huygens raciocinou da seguinte forma. Imagine um sulco na forma de uma ciclóide, como mostrado na Fig. 6.2.
Uma bola pesada rola ao longo deste sulco M. Consideraremos o caso ideal - o caso em que não há atrito e resistência do ar.
Denote os pontos de cúspide da ciclóide por M 0 e M? 0 , e o raio do círculo gerador através uma. Desenhe um círculo de raio uma tangente à ciclóide no vértice (círculo centrado O) e gerando um círculo na posição correspondente ao ponto M ciclóides (dadas pela linha tracejada). Digamos que colocamos a bola no ponto M 1 ranhura e solte-a sem um empurrão. Sob a influência da gravidade, ele vai rolar para baixo. Vamos estudar o movimento dele.
Qual será a velocidade da bola quando ela atingir o ponto M ciclóides? É fácil de calcular. Descendo do ponto M 1 ponto M, a bola consumirá alguma energia potencial. Esta perda de energia é igual ao produto do peso da bola mg(m -- peso da bola, g-- aceleração da gravidade) para "perda de altura", ou seja, sobre a diferença na altura da bola em posições M 1 e M, além disso, as alturas são medidas a partir de um determinado nível, por exemplo, do nível do solo. De qualquer nível que as alturas sejam contadas, sua diferença no nosso caso será igual ao segmento NM. Assim, a perda de energia potencial da bola será igual a mg· HM.
Mas, em virtude da lei da conservação da energia, a energia potencial perdida da bola se transformará na energia cinética de seu movimento, que, como você sabe, é igual a, se denotarmos a velocidade ainda desconhecida da bola. Igualando esta energia cinética com a energia potencial perdida, obtemos a equação
a partir do qual encontramos imediatamente o valor da velocidade desejada
A direção dessa velocidade também é fácil de determinar. Ele será direcionado tangencialmente à ciclóide, ou seja, ao longo do acorde ML(Fig. 6.2), onde eu- o ponto "mais baixo" do círculo gerador.
Estaremos interessados não tanto na velocidade em si, mas em sua projeção vertical, ou seja, "a velocidade de descida da bola", a taxa de variação de sua altura. Essa projeção vertical é fácil de calcular: é igual a, onde é o ângulo entre a corda ML e verticais. Acorde NO círculo com centro O, é obviamente igual e paralelo à corda ML e, portanto, o ângulo LMP igual ao ângulo GATO, o que se nota na Fig. 6.2. Então:
Vamos comparar o movimento irregular ao longo de uma ciclóide com o movimento uniforme ao longo de um círculo. Para isso, construímos um círculo auxiliar da seguinte forma: pelo vértice MAS ciclóide é desenhada perpendicularmente DE ANÚNCIOS(diâmetro do círculo com centro O), e através do ponto de partida M 1 do movimento da bola, um paralelo M 1 B é desenhado à sua base. Seja o ponto de intersecção dessas paralelas e perpendiculares denotado pela letra NO. O círculo construído sobre AB, como no diâmetro, e será o círculo auxiliar desejado. Ainda não está claro como exatamente é melhor do que outros círculos.
Vamos começar com o fato de que vamos conectar a componente vertical da velocidade da bola com os elementos do círculo auxiliar. Nós temos:
Porque NM = VC. De um triângulo AJA Nós temos:
Mas AT=2a porque , e, portanto,
Substituímos o valor do cosseno encontrado na expressão para SENHOR marcada com um asterisco (*). Nós temos:
A última raiz é igual à média proporcional entre os segmentos VC e AK, ou seja entre os segmentos da hipotenusa AB triângulo abc, em que este último é dividido pela altura SC. Mas essa média proporcional, de acordo com o conhecido teorema das linhas proporcionais em um triângulo retângulo, é exatamente igual à altura SC:
VK·AK=SK 2 .
Portanto, para o componente vertical SENHOR a velocidade da bola ao longo da ciclóide obtemos finalmente:
MP=· KS.
Quantidades uma e g dado a nós desde o início e não estão ligados a um ponto M, nem com sua posição inicial M 1 . Assim, o movimento da bola ao longo da ciclóide é completamente determinado pela corda KS círculo auxiliar, ou seja, posição do ponto final A PARTIR DE neste círculo.
Considere o movimento uniforme de um ponto A PARTIR DE ao longo de um círculo auxiliar com uma velocidade angular de radianos por segundo, ou seja, graus por segundo. Neste caso, a velocidade do ponto A PARTIR DE ao longo de um círculo será igual ao produto do raio do círculo pela velocidade angular, expressa em radianos (por segundo), ou seja, é igual a
Quão rápido o ponto está caindo? A PARTIR DE, Com que rapidez sua distância da linha reta muda? M 0 M? 0 com movimento uniforme do ponto A PARTIR DE em torno da circunferência? Isso é fácil de calcular.
Velocidade o movimento de um ponto do círculo é direcionado tangencialmente ao círculo, ou seja, perpendicular ao raio. Sua projeção na vertical é igual à própria velocidade multiplicado pelo cosseno do ângulo Fig. 6.3. Mas o ângulo é obviamente igual ao ângulo CSR 1: ambos são obtidos subtraindo o ângulo O 1 CE de um ângulo reto. Cosseno de um ângulo CSR 1 igual . Para a projeção vertical da velocidade do movimento uniforme em um círculo, encontramos:
Um resultado notável é obtido: quando um ponto se move uniformemente ao longo de um círculo, sua projeção na vertical se move exatamente da mesma maneira que a projeção na vertical de uma bola rolando ao longo de uma ciclóide. As projeções de ambas as velocidades em qualquer momento são iguais entre si. Mas segue-se disso que o ponto do círculo de NO dentro MAS e uma bola em uma ciclóide de M 1 em MAS virá ao mesmo tempo. Este tempo é fácil de determinar. Já dissemos que um ponto no círculo auxiliar faz radianos um segundo, ou seja, ele girará um radiano em segundos e radianos em. Exatamente o mesmo tempo é necessário para a nossa bola rolar a ciclóide do ponto M 1 ponto MAS. Ele levará o mesmo tempo para subir por inércia até o ponto M? 1 , o mesmo - descer novamente, e o mesmo - subir e retornar à posição inicial (ao ponto M 1). Isso significa que o tempo de oscilação total da bola (período de oscilação) será igual a:
Esta é uma fórmula muito maravilhosa. Vemos que o período de movimento da bola ao longo da ranhura cicloidal é completamente determinado pelas dimensões da ranhura (o raio do círculo gerador da cicloide) e pela aceleração da gravidade. Posição do ponto M 1 na ciclóide, sua distância da linha reta M 0 M? 0 isso não importa. De qualquer ponto da ciclóide que a bola comece a se mover, o período de sua oscilação será o mesmo.
Huygens pensou em como usar a propriedade tautócrona da ciclóide para construir um pêndulo "perfeito". Como fazer a bola do pêndulo se mover tautocronicamente sem recorrer a ranhuras e dispositivos similares com muito atrito? Pensando nisso, Huygens chegou aos conceitos de evoluta e involuta.
Vamos fazer um modelo consistindo em dois semi-arcos idênticos da ciclóide com uma cúspide comum O(Fig. 6.4). Denotamos o raio do círculo gerador, como sempre, por uma. Vamos fortalecer o modelo verticalmente e na cúspide O amarre um fio com um comprimento igual a 4 uma-- ou seja duas vezes o diâmetro do círculo gerador da ciclóide. linha final livre T dar-lhe uma bola pesada.
A bola descreverá durante seu movimento o desdobramento da ciclóide ASOEV, porque o fio irá envolver o modelo. Mas o desdobramento da ciclóide é exatamente a mesma ciclóide. Então a curva VMTRA, ao longo do qual a bola se move, será uma ciclóide gerada por um círculo de raio uma.
Se colocarmos a bola em um ponto arbitrário M e deixá-lo sozinho, ele começará a oscilar, e o período dessas oscilações não dependerá da escolha do ponto M. Mesmo que, sob a influência do atrito e da resistência do ar, a oscilação das oscilações diminua, o tempo de oscilação do pêndulo permanece inalterado. Verdadeiramente este pêndulo será tautócrono!
Consideremos agora pequenas oscilações do pêndulo ao longo do arco AB ciclóides (Fig. 6.5). Se essas oscilações forem muito pequenas, a influência do modelo de guia não será praticamente sentida e o pêndulo se moverá quase como um pêndulo comum com um comprimento eu=4uma, suspenso em um ponto O. Caminho AB pêndulo cicloidal praticamente não diferirá do caminho CE comprimento do pêndulo circular 4 uma. Isso significa que o período de pequenas oscilações de um pêndulo circular comum com comprimento eu=4uma praticamente não diferirá do período do pêndulo cicloidal. Entrando na fórmula
com a qual nos encontramos acima, em vez de uma igual a ele, obtemos a expressão para o período de pequenas oscilações de um pêndulo circular em função de seu comprimento:
CONCLUSÃO
No processo de conclusão do meu trabalho de curso, estudei materiais sobre o tema da ciclóide, estudei as características do melhor pêndulo, comparei o estudo bastante elegante, mas não muito simples, da ciclóide antes do advento do cálculo integral, com o mais simples e mais familiar, estudado em geometria diferencial e análise matemática; mais uma vez convencido da necessidade de estudar essas disciplinas. Como se viu, a ciclóide tem uma enorme aplicação prática não apenas em matemática, mas também em cálculos tecnológicos, em física.
O trabalho sobre o estudo deste tópico acabou sendo bastante emocionante e interessante.
BIBLIOGRAFIA
1. Berman G.N. Ciclóide. -M., 2007. -113s.
2. Savelov A.A. Curvas planas. - M., 1960. - 293 p.
3. Fikhtengolts G.M. Fundamentos de análise matemática. -M., 2005, v.2. -464 pág.
Hospedado em Allbest.ru
...Documentos Semelhantes
Breve história do estudo da ciclóide. Definição geométrica, propriedades e características da construção da ciclóide. Equação ciclóide paramétrica e equação em coordenadas cartesianas. Tarefas para encontrar partes de uma ciclóide e figuras formadas por uma ciclóide.
trabalho de conclusão de curso, adicionado em 16/01/2011
Momentos e centros de massa de curvas planas. Teorema de Gulden. A área da superfície formada pela rotação de um arco de uma curva plana em torno de um eixo que se encontra no plano do arco e não o intercepta é igual ao produto do comprimento do arco pelo comprimento do círculo.
palestra, adicionada em 04/09/2003
Definição de uma integral definida, suas propriedades. O comprimento do arco da curva. Área de um trapézio curvilíneo. Área de superfície de rotação. Áreas de figuras delimitadas por gráficos de funções delimitadas por linhas dadas por equações. Cálculo de volumes de corpos.
trabalho de controle, adicionado em 10/02/2017
Uma integral definida é um funcional normalizado monótono aditivo definido em um conjunto de pares, seus componentes, propriedades. Cálculo de uma integral definida; Fórmula de Newton-Leibniz. Aplicações geométricas: área, comprimento de arco, volume de um corpo de revolução.
apresentação, adicionada em 30/05/2013
Encontrando a área de uma figura limitada por gráficos de funções usando uma integral dupla. Obtenção por rotação do volume do corpo em torno do eixo OX da figura, limitado pelas linhas especificadas. Limites de integração em uma integral dupla sobre uma região delimitada por linhas.
teste, adicionado em 28/03/2014
Linhas notáveis da 3ª ordem: lista cartesiana, cissoide de Diocles, strofrid, verzier de Agnesi. Linhas da quarta ordem e superiores e algumas linhas transcendentais: a espiral de Arquimedes, a curva da descida mais curta. A área da área delimitada pela lemniscata.
trabalho de conclusão de curso, adicionado em 07/08/2015
O conceito de integral definida, o cálculo da área, o volume do corpo e o comprimento do arco, o momento estático e o centro de gravidade da curva. Cálculo de área no caso de uma região curvilínea retangular. Aplicação de integrais curvilíneas, de superfície e triplas.
trabalho de conclusão de curso, adicionado em 19/05/2011
Derivada de uma integral definida em relação a um limite superior variável. Cálculo de uma integral definida como limite da soma integral pela fórmula de Newton–Leibniz, mudança de variável e integração por partes. Comprimento do arco em coordenadas polares.
trabalho de controle, adicionado em 22/08/2009
História do cálculo integral e diferencial. Aplicações da integral definida à solução de alguns problemas de mecânica e física. Momentos e centros de massa de curvas planas, teorema de Gulden. Equações diferenciais. Exemplos de resolução de problemas no MatLab.
resumo, adicionado em 09/07/2009
Integrais curvilíneas de primeiro e segundo tipo. A área da área delimitada por uma curva fechada. O volume de um corpo formado pela rotação de uma curva fechada. Centro de massa e momentos de inércia da curva. Campo magnético em torno de um condutor de corrente. A essência da lei de Faraday.
Lembre-se daqueles oran-mesma-camada-massa-co-ka-ta-fo-você - luz-de-ra-zha-te-se, anexado-la-u-schi-e-sya às agulhas de tricô ve- lo-si-ped-no-go-ko-le-sa? At-cre-pim ka-ta-fot para sa-mo-mu rim-du ko-le-sa e siga seu tra-ek-to-ri-she. De acordo com as curvas lu-chen-nye, eles estão ligados à família do cicloid.
Ao mesmo tempo, Ko-le-so é chamado-zy-va-et-sya sobre-de-no-dia-círculo (ou círculo-stu) ciclo-lo-e-dy.
Mas vamos lá, vamos voltar ao nosso século e re-re-sya-dem em um tech-no-ku mais moderno. No caminho, tchau-ka, ka-mu-shek caiu, alguém ficou preso em um pro-tek-to-re ko-le-sa. Pro-ver-agora-shis algumas voltas com um co-le-som, onde-sim-le-tit ka-men, quando você é trapaceiro do pro-tek-to-ra? Contra a direita-le-ção do movimento do mo-o-ciclo-la ou na direita-le-ção?
De fato, movimento livre do corpo na-chi-na-et-sya de acordo com ka-sa-tel-noy para aquele tra-ek-that-rii, de acordo com o qual o enxame se moveu. Ka-sa-tel-naya para ciclo-lo-e-de sempre on-right-le-on on-right-le-tion do movimento e passa pelo ponto superior ku pro-de-in-dia-circle-no -sti. Na direção certa, o movimento do mesmo-le-tit e nosso ka-mu-shek.
Você se lembra de como você andava nas poças em sua infância em uma bicicleta-lo-si-pe-de sem asa traseira? Mok-para-lo-ka nas costas -ta-ta.
O século 17 é o século do ciclo-e-dy. Os melhores cientistas estudaram suas incríveis propriedades.
Algum tipo de tra-ek-to-riya traz o corpo, se move sob a ação da força da gravidade, de um ponto a outro por um curto período de tempo? Esta seria uma das primeiras tarefas daquele na-at-ki, alguém-paraíso nesta hora não-senta-no-nome do número va-ri-a-tsi-on-noe.
Mi-ni-mi-zi-ro-vat (ou mak-si-mi-zi-ro-vat) podem ser coisas diferentes - o comprimento do caminho, velocidade, tempo. No za-da-che sobre sutiã-hi-cem-crono mi-ni-mi-zi-ru-et-x nome-mas tempo -chame-em: grego βράχιστος - o menor, χρόνος - tempo).
A primeira coisa que vem à mente é um tra-ek-to-riya direto. Vamos lá, vamos também olhar para o re-re-ver-bem-thuyu cyclo-lo-and-du com o ponto de retorno-vra-ta na parte superior de for-given-th-check. E, seguindo Ga-li-leo Ga-li-le-em, - quatro-vert-tin-ku círculo-no-sti, conectando-nya-yu-shchy on-shi pontos.
Por alguma razão, Ga-li-leo Ga-li-ley ras-smat-ri-val four-vert-tin-ku círculos e considerou que este era o melhor no sentido le time-me-no tra-ek-that -riya descida-ka? Ele digitou lo-ma-nye e observou que, com o aumento do número de links, o tempo diminuirá. Daqui-sim, Ga-li-lei naturalmente foi para o círculo, mas chegou à conclusão errada de que esse tra-algo -ria é o melhor entre todos os possíveis. Como podemos ver, o melhor-shey tra-ek-to-ri-she é-la-et-sya cyclo-lo-e-sim.
Através de dois pontos dados, é possível passar um único ciclo-lo-e-du com a condição de que no ponto superior haja toch-ka vra-ta tsik-lo-e-dy. E sim, quando o ciclo-lo-e-de vier-ho-dit-sya sob-nenhuma-mãe-sya para passar pelo segundo ponto, ela ainda será a descida Cree-howl nai-sko-rei-she-go !
Outro for-da-cha de um-para-o-beauti-si-vaya, conectado com o ciclo-lo-e-doy, é o for-da-cha sobre ta-na-que-cron. Traduzido do grego, ταύτίς significa “o mesmo”, χρόνος, como já sabemos - “tempo”.
Vamos fazer três montanhas um-a-um com pró-filme na forma de ciclo-lo-e-dy, de modo que as extremidades das montanhas sejam coruja-pa-da-li e ras-po-la-ga -lis no topo do ciclo-lo-and-dy. Vamos colocar três bo-ba em diferentes você-assim-você e vamos-escurecer de-mash-ku. Fato Udi-vi-tel-ney-shiy - todo mundo iria descer um-agora-homens-mas!
No inverno, você pode construir uma montanha de gelo no quintal e conferir essa propriedade ao vivo.
For-da-cha sobre ta-at-that-chrono-st-it em na-ho-de-nii um uivo tão torto que, na-chi-naya de qualquer-bo-go-inicial- mas da mesma maneira , o tempo para descer até um determinado ponto será o mesmo.
Hri-sti-en Guy-gens do-ka-zal, que o único ta-na-que-cron-noy é-la-et-sya cyclo-lo-e-sim.
Ko-nech-mas, Guy-gen-sa não é descida in-te-re-so-val ao longo das montanhas geladas. Naquela época, os cientistas não tinham um crescimento tão grande para-sem-mãe-para-s-para-mi por amor à arte. Por-sim-chi, algum-centeio estudado, era-ho-di-li da vida e por-pro-corujas daqueles-não-ki daquele tempo-eu-não. No século 17, co-ver-sha-yut-sya já está distante dos planos marítimos. Shi-ro-tu mo-rya-ki você pode determinar-de-lyat já para-cem-preciso-mas-preciso-mas, mas surpresa-vi-tel-mas que você não sabe como determinar - de-lyat com-tudo. E um dos pré-la-gav-shih-s-so-bos de-me-re-niya shi-ro-you era os-no-van em na-li-chii crono-no-met-ditch preciso.
O primeiro, que para-du-pequeno de-lat ma-yat-no-no-know-s, alguém seria preciso, foi Ga-li-leo Ga-li-ley. No entanto, naquele momento em que ele na-chi-na-et eles re-a-li-zo-vy-vat, ele já está velho, ele é cego, e pelo ano restante o cientista não tem tempo para fazer uma assistir em sua vida. Ele za-ve-shcha-et este filho-bem, no entanto, aquele iluminado de mel e na-chi-na-et para-nenhuma-mãe-sya ma-yat-ninguém, o mesmo só per- pere- morte e não ter tempo para re-a-li-zo-vat para-nos-sentamos. O próximo sinal do enxame foi Christi-sti-an Guy-gens.
Ele observou que re-ri-od-ko-le-ba-niya geralmente-go ma-yat-ni-ka, ras-smat-ri-vav-she-go-sya Ga-li-le-em, por- wee-sentar de-para-o-começo-mas-do-lo-mesmo, i.e. de am-pli-tu-dy. Para-pensar sobre como-va deve ser um tra-ek-that-riya do movimento de uma carga, de modo que o tempo de ka-che-tion nela não -se-lo de am-pli-tu -dy, ele re-sha-et for-da-chu sobre ta-at-that-chron. Mas como mover a carga ao longo do ciclo-lo-e-de? Pe-re-vo-dya theo-re-ti-che-pesquisa-antes-va-ção no plano-ti-che-prático, Guy-gens de-la-et “bochechas”, em alguém-rye na- ma-you-va-et-sya ve-roar-ka ma-yat-no-ka, e re-sha-et mais algumas tarefas ma-te-ma-ti-che. Faz-ka-zy-va-et que as “bochechas” devem ter o perfil do mesmo ciclo-lo-e-dy, da mesma forma que evo-lu-aquele ciclo-lo-and-dy yav-la- et-sya ciclo-lo-e-sim com o mesmo pa-ra-met-ra-mi.
Além disso, a construção pré-lo-fêmea de Guy-gen-som do ciclo-lo-e-longe-no-go ma-yat-no-ka posa-in-la-et por -contar o comprimento de o ciclo-lo-e-dy. Se houver um azul-sem-ponto-ku, o comprimento-para-algum-enxame é igual a quatro-você-rem ra-di-u-sam sobre-de-em-dya-sche-go círculo, mak- si-mal-mas de-clo-fio, então seu fim será no ponto de re-re-se-che-niya “bochechas” e ciclo-lo-e-dy-tra-ek-to-rii, ou seja. no topo do ciclo-lo-e-dy-“cheek-ki”. Como isso é in-lo-vi-no comprimento de ar-ki ciclo-e-dy, então o comprimento total é igual a oito ra-di-u-sam pro-de-no-tio-ésimo círculo.
Christ-sti-an Guy-gens fez um ma-yat-nik cíclico-lo-e-distante, e horas com ele pro-ho-di-se é-py-ta-niya no mar pu-te-she- stvi-yah, mas não veio. No entanto, assim como os relógios com o habitual ma-yat-no-one para esses fins.
De-que, um-para-um, ainda su-sche-stu-yut cha-so-me-ha-bottom-nós com o habitual-mas-vein-ny ma-yat-ninguém? Se você olhar para ele, então com pequenos de-clo-não-no-yah, como o vermelho-não-vai ma-yat-no-ka, “bochechas” ciclo-lo-e-longe-mas-vai ma- yat-no-ka quase nenhuma influência de olho-zy-va-yut. Correspondentemente, o movimento ao longo do cíclico-lo-e-de e ao redor da circunferência com pequeno de-clo-no-no-yah é quase coruja-pa-sim-yut.
5. Equação paramétrica da ciclóide e a equação em coordenadas cartesianas
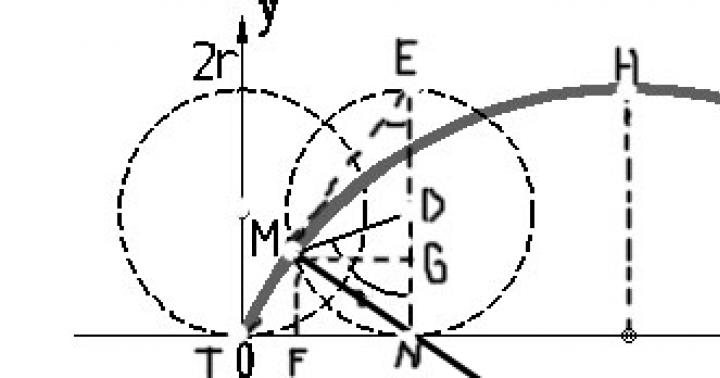
Suponha que temos uma ciclóide formada por um círculo de raio a centrado no ponto A.
Se escolhermos como parâmetro que determina a posição do ponto, o ângulo t=∟NDM pelo qual o raio conseguiu girar, que tinha uma posição vertical AO no início do rolamento, então as coordenadas xey do ponto M será expresso da seguinte forma:
x \u003d OF \u003d ON - NF \u003d NM - MG \u003d at-a sin t,
y= FM = NG = ND - GD = a - a custo t
Assim, as equações paramétricas da ciclóide têm a forma:

Ao mudar t de -∞ para +∞, você obtém uma curva que consiste em um conjunto incontável desses ramos, que é mostrado nesta figura.
Além disso, além da equação paramétrica da ciclóide, há também sua equação em coordenadas cartesianas:
Onde r é o raio do círculo que forma a ciclóide.
6. Problemas para encontrar partes de uma ciclóide e figuras formadas por uma ciclóide
Tarefa número 1. Encontre a área de uma figura limitada por um arco de uma ciclóide cuja equação é dada parametricamente
![]()
e eixo Oh.

Solução. Para resolver este problema, usamos os fatos que conhecemos da teoria das integrais, a saber:
A área do setor curvilíneo.
Considere alguma função r = r(ϕ) definida em [α, β].
ϕ 0 ∈ [α, β] corresponde a r 0 = r(ϕ 0) e, portanto, o ponto M 0 (ϕ 0 , r 0), onde ϕ 0 ,
r 0 - coordenadas polares do ponto. Se ϕ muda, “percorrendo” o todo [α, β], então o ponto variável M descreverá alguma curva AB dada por
a equação r = r(ϕ).
Definição 7.4. Um setor curvilíneo é uma figura limitada por dois raios ϕ = α, ϕ = β e uma curva AB dada em polar
coordenadas pela equação r = r(ϕ), α ≤ ϕ ≤ β.
A seguir
Teorema. Se a função r(ϕ) > 0 e é contínua em [α, β], então a área
setor curvo é calculado pela fórmula:

Este teorema foi provado anteriormente no tópico de uma integral definida.
Com base no teorema acima, nosso problema de encontrar a área de uma figura limitada por um arco da ciclóide, cuja equação é dada pelo paramétrico x= a (t - sin t) , y= a ( 1 - cos t) , e o eixo Ox, é reduzido para a seguinte solução .
Solução. Da equação da curva dx = a(1−cos t) dt. O primeiro arco da ciclóide corresponde à mudança no parâmetro t de 0 para 2π. Consequentemente,

Tarefa número 2. Encontre o comprimento de um arco da ciclóide
![]()
O seguinte teorema e seu corolário também foram estudados em cálculo integral.
Teorema. Se a curva AB é dada pela equação y = f(x), onde f(x) e f '(x) são contínuas em , então AB é retificável e
Consequência. Seja AB dado parametricamente
LAB = ![]() (1)
(1)
Sejam as funções x(t), y(t) continuamente diferenciáveis em [α, β]. Então
fórmula (1) pode ser escrita como

Vamos fazer uma mudança de variáveis nesta integral x = x(t), então y'(x)= ;
dx= x'(t)dt e, portanto:

Agora vamos voltar a resolver nosso problema.
Solução. Temos e portanto
Tarefa número 3. É necessário encontrar a área de superfície S formada a partir da rotação de um arco da ciclóide
L=((x,y): x=a(t - sin t), y=a(1 - custo), 0≤ t ≤ 2π)
No cálculo integral, existe a seguinte fórmula para encontrar a área da superfície de um corpo de revolução em torno do eixo x de uma curva dada parametricamente em um segmento: x=φ(t), y=ψ(t) (t) 0 ≤t ≤t 1)
Aplicando esta fórmula à nossa equação ciclóide, obtemos:

Tarefa número 4. Encontre o volume do corpo obtido pela rotação do arco da ciclóide
![]()
Ao longo do eixo Ox.
No cálculo integral, ao estudar volumes, há a seguinte observação:
Se a curva que limita o trapézio curvilíneo é dada por equações paramétricas e as funções nestas equações satisfazem as condições do teorema sobre a mudança de variável em uma certa integral, então o volume do corpo de rotação do trapézio em torno do eixo Ox será ser calculado pela fórmula

Vamos usar esta fórmula para encontrar o volume que precisamos.
Problema resolvido.
Conclusão
Assim, no decorrer deste trabalho, foram esclarecidas as principais propriedades da ciclóide. Eles também aprenderam a construir uma ciclóide, descobriram o significado geométrico da ciclóide. Como se viu, a ciclóide tem uma enorme aplicação prática não apenas em matemática, mas também em cálculos tecnológicos, em física. Mas a ciclóide tem outros méritos. Foi usado por cientistas do século 17 no desenvolvimento de métodos para estudar linhas curvas, aqueles métodos que eventualmente levaram à invenção do cálculo diferencial e integral. Foi também uma das "pedras de toque" sobre as quais Newton, Leibniz e seus primeiros pesquisadores testaram o poder de novos métodos matemáticos poderosos. Finalmente, o problema da braquistócrona levou à invenção do cálculo de variações, tão necessário para os físicos de hoje. Assim, a ciclóide estava inextricavelmente ligada a um dos períodos mais interessantes da história da matemática.
Literatura
1. Berman G.N. Ciclóide. - M., 1980
2. Verov S.G. Braquistócrona, ou outro segredo da ciclóide // Kvant. - 1975. - Nº 5
3. Verov S.G. Segredos da ciclóide// Kvant. - 1975. - Nº 8.
4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Aplicações de uma integral definida. Orientações e trabalhos individuais para alunos do 1º ano da Faculdade de Física. - Rostov n/a: UPL RSU, 1994.
5. Gindikin S.G. Idade estelar de uma ciclóide // Kvant. - 1985. - Nº 6.
6. Fikhtengolts G.M. Curso de cálculo diferencial e integral. T.1. - M., 1969
Essa linha é chamada de "envelope". Toda linha curva é o envelope de suas tangentes.
Matéria e movimento, e o método que eles constituem, permitem que todos realizem seu potencial no conhecimento da verdade. O desenvolvimento de uma metodologia para o desenvolvimento de uma forma de pensamento dialético-materialista e o domínio de um método de cognição semelhante é o segundo passo para resolver o problema do desenvolvimento e realizar as possibilidades do Homem. Fragmento XX Oportunidades...
A situação pode adoecer com neurastenia - neurose, cuja base do quadro clínico é uma condição astênica. Tanto no caso da neurastenia quanto no caso da descompensação da psicopatia neurastênica, a essência da proteção espiritual (psicológica) é manifestada por um desvio das dificuldades para uma fraqueza irritável com disfunções vegetativas: ou uma pessoa inconscientemente “revida” mais de um ataque ...





Vários tipos de atividades; desenvolvimento da imaginação espacial e das representações espaciais, pensamento figurativo, espacial, lógico, abstrato de escolares; a formação de habilidades para aplicar conhecimentos e habilidades geométricas e gráficas para resolver vários problemas aplicados; familiarização com o conteúdo e a sequência de etapas das atividades do projeto no campo das técnicas e ...
Arcos. Espirais também são involutas de curvas fechadas, como a involuta de um círculo. Os nomes de algumas espirais são dados pela semelhança de suas equações polares com as equações de curvas em coordenadas cartesianas, por exemplo: espiral parabólica (a - r)2 = bj, espiral hiperbólica: r = a/j. Rod: r2 = a/j si-ci-espiral, cujas equações paramétricas se parecem com: , )