Exibições (funções)

As funções desempenham um papel central na matemática, onde são usadas para descrever qualquer processo pelo qual elementos de um conjunto são de alguma forma transformados em elementos de outro. Tais transformações de elementos são uma ideia fundamental e de suma importância para todos os processos computacionais.

Definição. A relação f em AB é chamada mapeamento (função) de A a B se para cada xA existe um e apenas um yB. definir equivalência de relação binária

f: AB ou y=f(x)

O conjunto A é chamado domínio de definição. Conjunto B - variar.

Se y=f(x), então x é chamado argumento, e y- valor da função.

Seja f: AB, então

conjunto de definição recursos:

conjunto de valores recursos:

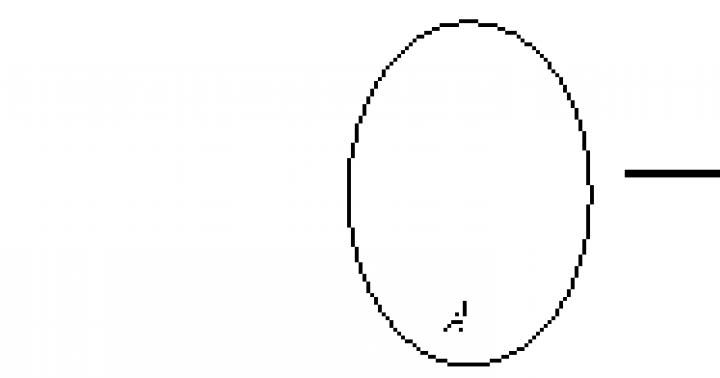
O conjunto de definição de função é um subconjunto do domínio de definição, ou seja, Dom f A, e o conjunto de valores de função é um subconjunto do intervalo de função, ou seja, Im f B. Se, então a função é chamada total, e se, parcial. Assim, um diagrama de Venn serve como uma ilustração conveniente de uma função definida no conjunto A com valores no conjunto B.

Maneiras de definir uma função:

• 1) Verbal.
• 2) Analítico.
• 3) Com a ajuda de um gráfico, um desenho.
• 4) Com a ajuda de tabelas.

Definição. Se MA, então o conjunto f(M)=y f(x)=y para algum x de M é chamado caminho define M.

Se KB, então o conjunto f -1 (K)=x f(x)K é chamado protótipo define K.

Definição A função é chamada de função de n argumentos ou função de n-lugares. Tal função mapeia uma tupla para um elemento bB, .

Propriedades dos mapeamentos (funções).

1) O mapeamento f:AB é chamado injetor, se mapear elementos diferentes de A para elementos diferentes de B: .

Essa propriedade pode ser mostrada usando diagramas de Venn.

2) O mapeamento f:AB é chamado sobrejetivo ou mapeamento para todo o conjunto B, se pelo menos um elemento de A for mapeado para cada elemento do conjunto B: .

Essa propriedade também pode ser mostrada usando diagramas de Venn.

3) Um mapeamento f: AB que é tanto injetivo quanto sobrejetivo é chamado bijetivo ou um mapeamento um-para-um de um conjunto A em um conjunto B.

Exemplo. Seja dado um mapeamento f:RR, que é definido de tal forma que. Descubra quais propriedades esse mapeamento possui.

Solução. A função f não é injetiva, porque f(2)=f(2), mas 2 2.

A função f também não é sobrejetiva, pois não existe um número real x para o qual f (x) = 1.

Definição. Seja f um mapeamento bijetivo de um conjunto A para um conjunto B. Se associarmos cada elemento de B com um elemento associado de A, então tal correspondência é um mapeamento de B para A. Este mapeamento é denotado e chamado mapeamento inverso ao mapeamento f.

O mapeamento inverso tem algumas propriedades, que formulamos no seguinte teorema.

Teorema 3. Se f: AB é uma bijeção, então

1) para qualquer y de B;

2) para qualquer x de A.

Prova. 1) Seja yB e. Então f(x)=y. Mas desde

2) Prova-se similarmente que para qualquer x de A.

Definição. Composição (superposição, produto) mapeamentos f:AB eg:BC é chamado de mapeamento h: , que é escrito h=g f.

Essa forma de escrever a superposição de funções é explicada pelo fato de que a designação da função geralmente é escrita à esquerda da lista de argumentos:

O conceito de mapeamento de conjuntos desempenha um papel importante em todas as áreas da matemática.

Definição 1. Deixe X e S são alguns conjuntos e. Se cada elemento
correspondeu a um e apenas um elemento
, então eles dizem que dado exibição de X dentro S com área de tarefa A .

Os mapeamentos geralmente são indicados por pequenas letras latinas
.

Exemplo 1. Deixe Xé o conjunto dos números naturais. Cada número
colocar em correspondência o resto de sua divisão por 2:
. Obtenha um mapeamento de X no conjunto dos números reais R, em que cada
corresponde a 0 ou 1.

Vários X também chamado muitas partidas , e o conjunto S –muitas chegadas .

Definição 2. Elemento
, correspondente ao elemento
em exibição f, é chamado caminho elemento X e denotado
. No entanto, o próprio elemento X chamado protótipo elemento no. Se um MAS– área de tarefas quando exibida f, então o conjunto é chamado conjunto A quando exibido f ou variar exibição f.

Definição 3. Se a área de tarefa for igual à área de partida, ou seja,
, então f é chamado de mapeamento X dentro S designar
. Se um
, então f é chamado de mapeamento XnoS.

Definição 4. Exibição
chamado reversível se elementos diferentes

, ou seja para qualquer
temos
.

Por exemplo, exibir
com área de trabalho R não é reversível porque
e
, ou seja
, Apesar
.

Definição 5. Mapeamento reversível X no S chamado um a um exibição.

Ilustraremos os conceitos introduzidos com figuras.

f não é uma exibição

Deixar f é um mapeamento invertível de X dentro S com área de trabalho MAS. Então cada elemento
corresponde a um e apenas um elemento
, e vários elementos
combinar diferentes elementos no. Portanto, o mapeamento
conjuntos
dentro X(no MAS). Definido para que.

Definição 6. Se exibir f a partir de X dentro S reversível, então o mapeamento
a partir de S dentro X, definido pela razão, é chamado reverter para f .

Vamos agora f- exibição X dentro S, uma g- exibição S dentro Z. Vamos definir o mapeamento X dentro Z Da seguinte maneira:. Nesse caminho,
, isso é
. Tal exibição é chamada composição mapeamentos f e g e denotado
. Então para todos

A operação de composição de mapeamento tem as seguintes propriedades.

Associatividade:

Com efeito, se
, então

.

De fato, deixe
e
. Por causa da reversibilidade f
. Por causa da reversibilidade g e, portanto, a exibição
reversível. Se um
, então
, que é o que era necessário para ser provado.

A função real é um caso especial de mapeamento quando os conjuntos X e S são conjuntos numéricos.

Definição 7. Deixe X - conjunto de números. Exibição
, correspondendo a cada número
número
, é chamado válido função definida no set X. Em que X chamado argumento funções f,X–seu escopo ,
–valor funções. Vários
chamado conjunto de valores funções.

Definição 8. Se funcionar f corresponde a cada número
o mesmo valor uma, então a função f chamado constante .

Segue da definição de uma função real que para definir uma função f é necessário definir seu domínio de definição - um conjunto X e a lei pela qual todo número
o número é correspondido
.

Dependendo de como a lei da dependência funcional é especificada, existem várias maneiras de especificar uma função.

maneira analítica. A lei da dependência funcional é especificada usando uma fórmula que indica quais ações precisam ser executadas no argumento X para obter o valor da função.

Exemplos:
etc.

No caso de uma forma analítica de definir uma função, o conjunto X muitas vezes não indicado. Nesse caso, o domínio da função é natural o escopo de uma função é o conjunto de valores de argumentos para os quais a expressão analítica fornecida faz sentido.

Por exemplo, para a função
domínio
, para a função
.

Se uma função reflete a relação entre quantidades específicas (físicas, geométricas e outras), então a área de sua definição pode não coincidir com a área onde a fórmula faz sentido. Por exemplo, a função
, considerado abstratamente, é definido em R, mas se expressa a lei da queda livre de um corpo, então
.

Observe que uma função pode ser definida não por uma, mas por várias fórmulas.

Por exemplo,
Para este recurso
.

forma tabular. Com esse método de configuração, a lei da dependência funcional é estabelecida por uma tabela na qual os valores correspondentes da função são comparados a diferentes valores do argumento.

O método tabular é usado em estudos experimentais, quando, por exemplo, as leituras do instrumento são feitas em determinados intervalos.

São compiladas tabelas de valores de muitas funções, que são frequentemente usadas em cálculos técnicos, que permitem encontrar os valores das funções sem cálculos.

A desvantagem do método tabular é que na tabela você pode encontrar os valores da função apenas para aqueles valores do argumento que estão nela. Outros valores podem ser encontrados por interpolação aproximadamente.

Maneira gráfica.

Definição 9.cronograma funções
definido no set X, é o conjunto de todos os pontos do plano
, cujas coordenadas X e no relacionado pela razão
. Igualdade
chamado equação este gráfico.

Uma função é considerada dada graficamente se seu gráfico for desenhado. Por exemplo, para medir a pressão atmosférica em diferentes altitudes, é usado um aparelho especial de auto-gravação - um barógrafo, que registra a mudança na pressão em função da altitude como uma curva em uma fita em movimento.

Nem toda curva pode servir como gráfico de alguma função. É necessário que não contenha quaisquer dois pontos com as mesmas abcissas.

Curva define Curva não define

função sem função

A vantagem do método gráfico de definir uma função sobre outras está na clareza, a desvantagem é que os valores da função só podem ser encontrados aproximadamente. Nem todas as funções podem ser representadas graficamente. Por exemplo, é impossível representar graficamente a função Dirichlet (Peter Gustav Lejeune-Dirichlet (1805-1859) - matemático alemão)

uma vez que entre quaisquer dois valores X existem infinitos pontos racionais e irracionais.

maneira verbal. A função é dada em palavras. Por exemplo, a parte inteira de um número Xé o maior inteiro que não excede X.

Definição 10. Funções
e
, dado em algum intervalo X, são chamados identicamente igual neste intervalo:
, se seus valores em cada ponto
Combine.

Exemplo. As funções são idênticas?

1)
e
;

2)
e
por
;

3)
e
?

Solução. 1), i.e., i.e. as funções são idênticas.

2) por propriedade
.

3), ou seja.
, as funções não são identicamente iguais.

Um papel importante na matemática é o estabelecimento de ligações entre dois conjuntos e associado à consideração de pares de objetos formados a partir de elementos do primeiro conjunto e dos elementos correspondentes do segundo conjunto. A exibição de conjuntos é de particular importância.

Sejam conjuntos arbitrários. exibindo conjuntos X para definir S qualquer regra é chamada f, segundo o qual cada elemento do conjunto está associado a um elemento bem definido (único) do conjunto .

O fato de que f existe um mapeamento , escrito resumidamente como: .

A notação também é usada. Mais frequentemente, os displays são indicados por letras f, q, F.

Então, para definir a exibição do conjunto X em um conjunto, cada elemento deve estar associado a um e apenas um elemento.

Se ao mesmo tempo o elemento X a partir de X elemento correspondente de S, então chamado elementos , uma X – pré-imagem do elemento ao exibir , que é escrito como .

Segue-se da definição de mapeamento que cada elemento de X a imagem é única, no entanto, para um elemento pode haver muitos protótipos, ou pode não existir. O conjunto de todas as pré-imagens de um elemento é chamado de protótipo completo e é denotado por . Nesse caminho, .

A imagem de um subconjunto de MAS e pré-imagem de um subconjunto de NO quando exibido:

Por exemplo, seja e seja um mapeamento MAS dentro MAS, que mapeia para cada elemento uma a partir de MAS resto da divisão uma para o número 4. Então temos:

Dependendo das propriedades, imagens e pré-imagens, os mapeamentos são sobrejetivos, injetivos e bijetivos.

A exibição é chamada sobrejetivo , se aqueles. cada elemento de exibe pelo menos um elemento de X, ou para qualquer .

A exibição é chamada injetor se diferentes elementos do conjunto X são mapeados para diferentes elementos do conjunto, ou seja, , ou está vazio ou um conjunto de um elemento para qualquer . Os mapeamentos injetivos também são chamados investimentos .

A exibição é chamada bijetivo , ou um a um mapeando se é sobrejetivo e injetivo, ou seja, se houver um conjunto de um elemento para qualquer . Nesse caso, os mapeamentos podem ser definidos definindo para qualquer : . É chamado marcha ré para e é denotado como .

Para maior clareza, descrevemos os tipos de mapeamentos.

Sobrejetivo Injetivo Bijetivo

Figura 12

Definir exibição MAS em si é chamado definir transformação MAS. Transformação bijetiva de um conjunto MAS chamado definir substituição MAS.

Um exemplo de substituição de um conjunto de inteiros é o mapeamento definido pela igualdade .

Observe também que o mapeamento do conjunto MAS dentro NO também chamado função definido no set MAS com valores no conjunto NO. O elemento é chamado valor funções ponto uma. O próprio conjunto MAS chamado área definições funções, e o conjunto é o intervalo da função.

Uma função é frequentemente tratada como uma variável que recebe valores de NO e tão dependente da variável X, que recebe valores de MAS, que cada valor uma variável X corresponde a um valor bem definido da quantidade . Ao mesmo tempo, escrevem e em vez de “função” dizem “função”.

Considere vários mapeamentos e defina seus tipos.

1) Deixe Xé o conjunto das circunferências do plano. Associando cada círculo ao seu centro, obtemos o mapeamento X no . Este mapeamento não é injetivo, pois um mesmo ponto pode ser o centro de um número infinito de círculos. Mas é sobrejetivo, pois qualquer ponto é o centro de algum círculo. Portanto, a correspondência inversa é definida em todos os lugares, sobrejetivamente, mas não funcionalmente.

2) Correspondência é uma função numérica dada em todo o conjunto de números reais. O conjunto de valores desta função é um conjunto de números não negativos. Como , a função não é sobrejetora. Também não é injetivo, pois . Portanto, não tem função inversa.

3) O mapeamento é sobrejetivo e injetivo: para qualquer existe um e apenas um número tal que . Este número é .

4) O mapeamento (é o conjunto de números não negativos) de um conjunto em si mesmo é definido em toda parte, injetivo, mas não sobrejetivo. De fato, para a fração , temos .

Portanto, o conjunto de valores dessa função é o intervalo. A função inversa é definida neste intervalo e assume valores não negativos.

5) O mapeamento definido pela regra é um mapeamento injetivo. Não é bijetivo porque . No entanto, se definirmos o mapeamento da mesma maneira, obteremos um mapeamento bijetivo. . ; sobrejetividade implica apenas sobrejetividade, e injetividade implica apenas injetividade.

3. Se e são transformações definidas MAS, então sua composição também é uma transformação do conjunto MAS.

Sejam $X$ e $Y$ dois conjuntos arbitrários.

Definição. Chama-se uma correspondência em que cada um dos elementos do conjunto $X$ está associado a um único elemento do conjunto $Y$ mapeamento.

O mapeamento do conjunto $X$ para o conjunto $Y$ é denotado por $X \stackrel(f)(\longrightarrow) Y$.

O conjunto $X$ é chamado domínio de definição mapeamento e é denotado por $X=D(f)$.

$E(f)$ é chamado conjunto de valores mapas e $E(f) = \( y \in Y \; | \; \exists x \in X, y = f(x) \)$.

O conjunto $\Gamma(f)$ é chamado cronograma exibição. $\Gamma(f)=\((x,y) \in X \times Y, y=f(x), \forall x \in X, y \in Y \)$.

Seja $f$ algum mapeamento do conjunto $X$ para o conjunto $Y$. Se $x$ for mapeado para $y$ neste mapeamento, então $y=f(x)$. Aqui $y$ é chamado caminho$x$, ou valor mapeando $f$ no ponto $x$. E $x$, respectivamente, protótipo elemento $y$.

Com base na definição do mapeamento, fica claro que não é necessário que todos os elementos do conjunto $Y$ sejam imagens de algum $x$ e, além disso, únicos.

Exemplo.

Dados dois conjuntos $X=\( c, e, n, m, i, b, p, b \)$ e $Y=\( 1, 2, 3, 4, 5, 9, 10, 11 \)$

O mapeamento do conjunto $X$ para o conjunto $Y$ tem a seguinte forma:

$\begin(matriz) \( c, & e, & n, & t, & i, & b, & p, & b \) \\ \;\; \updownarrow & \updownarrow & \updownarrow & \updownarrow & \updownarrow & \updownarrow & \updownarrow & \updownarrow \;\; \\ \( 1, & 2, & 3, & 4, & 5, & 9, & 10, & 11 \) \end(matrix)$

Definição. O conjunto de todos os elementos do conjunto $X$ cuja imagem é $y$ de $Y$ é chamado protótipo completo$y$ de $X$. Denotado: $f^(-1)(y)$.

Definição. Seja $A \subconjunto X$. O conjunto de todos os elementos $f(a)$, $a \in A$, é chamado na íntegra define $A$ sob o mapeamento $f$.

Definição. Seja $B \subconjunto Y$. O conjunto de todos os elementos de $X$ cujas imagens pertencem ao conjunto $B$ é chamado de imagem inversa completa do conjunto $B$.

Exemplo.

$X=Y=R$, $y=x^2$.

$A=[-1; 1]\subconjuntoX$

Imagem completa $f(A)=$

$B= \subconjunto Y$

Pré-imagem completa $f^(-1)(B)=[-1; 1]$

Definição. O mapeamento $f$ é chamado injetor mapeamento se $\forall \; y \in Y$ $y=f(x)$ é a imagem do único $x$.

Definição. O mapeamento $f$ é chamado sobrejetivo mapeamento se todos os elementos do conjunto $Y$ forem imagens de algum $x$. (Este é um mapeamento do conjunto $X$ no conjunto $Y$).

Definição. O mapeamento $f$ é chamado bijetivo, se for injetivo e sobrejetivo, caso contrário tal mapeamento é chamado de correspondência um-para-um.

Definição. Os conjuntos $X$ e $Y$ são chamados equivalente(equivalente) se estiverem em correspondência um-para-um. Denotado: $X Y$ (o conjunto $X$ é equivalente ao conjunto $Y$ ou o conjunto $X$ é equivalente ao conjunto $Y$).

1. Gráfico de conformidade. Exibição. Injetivo, não sobrejetivo.

Vamos agora estudar algumas questões relacionadas com as relações entre conjuntos.

Diremos que entre os conjuntos atitude(e estão em relação) se alguns (possivelmente todos) elementos de de correspondem a alguns elementos de. Se um conjunto está em relação a um conjunto, então escreveremos:

Se, neste caso, um elemento estiver associado a um elemento, denotaremos isso

Definição 1.1.2. A relação entre conjuntos é chamada mapeamento, se cada um estiver associado a um e apenas um elemento de (ver Fig. 1.1.2. e 1.1.3). Com a especialização da natureza do conjunto, surgem tipos especiais de mapeamentos, que têm os nomes especiais “função”, " vector-função", "operador", "medida", "funcional", etc. Vamos encontrá-los mais tarde.

Para denotar uma função (mapeamento) de w, usaremos a notação

Fig.1.1.2. Exibir Fig.1.1.3. Relação que não é

mapeamento

Definição 1.1.3. Se é um elemento de, então o elemento correspondente é chamado de sua imagem (quando exibido), e o conjunto de todos aqueles para os quais é chamado de pré-imagem e é denotado (ver Fig. 1.1.4).

Fig.1.1.4. protótipob

Definição 1.1.4. A exibição é chamada mapeamento de um para um, se cada elemento de from tiver uma imagem exclusiva no mapeamento e cada elemento tiver uma pré-imagem exclusiva nesse mapeamento.

Fig.1.1.5. Mapeamento de um para um

A seguir, consideraremos apenas mapeamentos, pois existem truques que reduzem mapeamentos multivalorados a valores únicos, que chamamos simplesmente de mapeamentos.

O conceito de mapeamento desempenha um papel crucial na matemática; em particular, na análise matemática, o lugar central é ocupado pelo conceito funções, que é um mapeamento de um conjunto de números para outro.

1.7. Definir potência

Ao estudar as relações entre conjuntos, o "volume" dos conjuntos, o número de elementos neles, é de grande interesse. Mas falar sobre o número de elementos é compreensível e justificado se esse número for finito. Conjuntos que consistem em um número finito de elementos serão chamados final . No entanto, muitos dos conjuntos considerados na matemática não são finitos, por exemplo, o conjunto dos números reais, o conjunto dos pontos no plano, o conjunto das funções contínuas definidas em algum segmento, etc. Para caracterizar quantitativamente conjuntos infinitos (e finitos) na teoria dos conjuntos, o conceito é usado cardinalidade do conjunto .

Diremos que os conjuntos e temos mesmo poder , se houver um mapeamento um para um de um conjunto para um conjunto (observe que nesse caso também existe um mapeamento um para um de um conjunto B para um conjunto A).

Se os conjuntos u têm a mesma cardinalidade, dizemos que eles são equivalentes , isto é denotado por: .

Sejam conjuntos arbitrários, então

Essa. qualquer conjunto é equivalente a si mesmo; se um conjunto é equivalente a um conjunto, então é equivalente; se, finalmente, um conjunto é equivalente a um conjunto que é equivalente a um conjunto, então é equivalente.

Um conjunto equivalente a alguns de seus próprios subconjuntos é chamado sem fim .

Se os conjuntos finitos têm diferentes números de elementos, fica claro que um deles contém menos elementos que o outro. Mas como comparar conjuntos infinitos nesse sentido? Dizemos que a cardinalidade de um conjunto é menor que a cardinalidade de um conjunto se existe um subconjunto do conjunto que é equivalente ao conjunto, mas os próprios conjuntos não são equivalentes.

Cardinalidade de um conjunto finito é igual ao número de seus elementos. Para conjuntos infinitos, o conceito de "potência" é uma generalização do conceito de "número de elementos".

Vamos apontar algumas classes de conjuntos que são úteis para o que segue.

O conjunto é chamado contável. , se tiver a mesma cardinalidade de algum subconjunto do conjunto (o conjunto dos números naturais). Um conjunto contável pode ser finito ou infinito.

Um conjunto infinito é enumerável se e somente se for equivalente ao conjunto dos números naturais.

Observe que qualquer conjunto cuja cardinalidade seja menor que a cardinalidade de um conjunto contável infinito é finito.

O conjunto dos números reais no intervalo de zero a um tem poder contínuo , e é frequentemente chamado contínuo . A cardinalidade deste conjunto é maior do que a cardinalidade de um conjunto infinito contável. Surge a questão: existe um conjunto cuja cardinalidade é maior que a cardinalidade de um conjunto infinito contável, mas menor que a cardinalidade do continuum. Este problema foi formulado em 1900 por um dos maiores matemáticos do mundo, David Hilbert. Descobriu-se que esse problema tem uma resposta um tanto inesperada: podemos supor que tal conjunto existe ou podemos supor que ele não existe. As teorias matemáticas resultantes serão consistentes. A prova deste fato foi apresentada pelo cientista americano Cohen em 1965 no Congresso Mundial de Matemáticos em Moscou. Observe que a situação com este problema se assemelha à situação com o quinto postulado de Euclides: através de um ponto situado fora de uma dada linha, apenas uma linha paralela à dada pode ser desenhada. Como mostrou Lobachevsky, a rejeição desse postulado não leva a contradições. Podemos construir uma geometria para a qual este postulado é válido e geometrias para as quais não é verdade.

Em conclusão, damos vários exemplos demonstrando a técnica para provar a equivalência de conjuntos.

Exemplo 1.11. O conjunto de inteiros é contável.

É claro que o conjunto considerado é infinito (o conjunto dos números naturais é seu subconjunto).

Para provar a enumerabilidade do conjunto dos inteiros, é necessário construir um mapeamento um-para-um entre o conjunto dos números naturais e o conjunto em consideração. O mapeamento necessário é dado pela regra: organizamos os inteiros da seguinte forma:

e renumere-os com números naturais, atribuindo-lhes números (estão indicados ao lado dos inteiros considerados). Obviamente, cada número inteiro terá seu próprio número, com números diferentes obtendo números diferentes. A recíproca também é verdadeira: para cada número natural (para cada número) há também um único inteiro sob esse número. Assim, o mapeamento um-para-um necessário foi construído.

Exemplo 1.12. O conjunto dos números racionais é enumerável.

Sabe-se que qualquer número racional pode ser representado como uma fração irredutível p/q, usando esta representação organizamos os números racionais de acordo com o esquema:

. . . . . .

Vamos renumerar esses números da mesma maneira que no exemplo anterior (os números são indicados na parte superior entre parênteses ao lado dos números). É fácil ver que a regra formulada para numerar números racionais fornece o mapeamento um a um necessário do conjunto dos números naturais no conjunto dos números racionais.

Exemplo 1.13. A união de um conjunto contável de conjuntos contáveis ​​é um conjunto contável.

A prova deste fato é semelhante à prova da afirmação do exemplo anterior.

Em conclusão, apresentamos uma afirmação importante para o que se segue. Mas para isso precisamos de mais uma operação em conjuntos.

Produto direto de conjuntos e( produto cartesiano ) é o conjunto de todos os pares ordenados , onde e. Este conjunto é rotulado. Nesse caminho:

Denote , o produto de fatores será denotado.

Teorema 1.1. para qualquer conjunto infinito Além disso.

Em particular, ou seja, o conjunto de pontos na linha tem a mesma cardinalidade que o conjunto de pontos no plano. Além disso, existem tantos pontos no espaço quanto em uma linha reta.

Isso conclui nosso conhecimento dos conceitos básicos da lógica matemática e da teoria dos conjuntos - os fundamentos da matemática moderna. Notamos que, infelizmente, muitos aspectos dessas teorias permaneceram fora do escopo deste capítulo; você pode se familiarizar com eles, por exemplo, por e .