Visualizzazione: questo articolo è stato letto 32852 volte
Pdf Seleziona lingua... Russo Ucraino Inglese
Breve recensione
Il materiale completo viene scaricato sopra, dopo aver selezionato la lingua
- Statica
- Concetti base di statica
- Tipi di forza
- Assiomi della statica
- Connessioni e loro reazioni
- Sistema di forze convergenti
- Metodi per la determinazione del sistema risultante di forze convergenti
- Condizioni di equilibrio per un sistema di forze convergenti
- Momento della forza rispetto al centro come vettore
- Valore algebrico del momento di forza
- Proprietà del momento di forza attorno al centro (punto)
- Teoria delle coppie di forze
- Somma di due forze parallele nella stessa direzione
- Addizione di due forze parallele dirette verso l'interno lati diversi
- Coppie di potenza
- Coppia di teoremi delle forze
- Condizioni per l'equilibrio di un sistema di coppie di forze
- Leva
- Sistema di forze piano arbitrario
- Casi di riduzione di un sistema piano di forze a una forma più semplice
- Condizioni di equilibrio analitico
- Centro delle forze parallele. Centro di gravità
- Centro delle forze parallele
- Il baricentro di un corpo rigido e le sue coordinate
- Centro di gravità del volume, dei piani e delle linee
- Metodi per determinare la posizione del baricentro
- Nozioni di base sulle racchette di forza
- Problemi e metodi di resistenza dei materiali
- Classificazione del carico
- Classificazione degli elementi strutturali
- Deformazioni dell'asta
- Principali ipotesi e principi
- Forze interne. Metodo di sezione
- Voltaggio
- Tensione e compressione
- Caratteristiche meccaniche del materiale
- Sollecitazioni ammissibili
- Durezza del materiale
- Grafici delle forze longitudinali e delle sollecitazioni
- Spostare
- Caratteristiche geometriche delle sezioni
- Torsione
- piegare
- Dipendenze differenziali in flessione
- Resistenza alla flessione
- sollecitazioni normali. Calcolo della forza
- Sforzi di taglio in flessione
- Rigidità alla flessione
- Elementi di teoria generale dello stato tensionale
- Teorie della forza
- Piegatura con torsione
- Cinematica
- Cinematica puntuale
- Traiettoria punto
- Metodi per specificare il movimento di un punto
- Velocità del punto
- accelerazione puntiforme
- Cinematica del corpo rigido
- Moto traslatorio di un corpo rigido
- Moto rotatorio di un corpo rigido
- Cinematica dei meccanismi ad ingranaggi
- Moto piano-parallelo di un corpo rigido
- Movimento punto complesso
- Cinematica puntuale
- Dinamica
- Leggi fondamentali della dinamica
- Dinamica puntuale
- Equazioni differenziali di un punto materiale libero
- Due problemi di dinamica puntuale
- Dinamica del corpo rigido
- Classificazione delle forze agenti su un sistema meccanico
- Equazioni differenziali del moto di un sistema meccanico
- Teoremi generali della dinamica
- Teorema sul moto del centro di massa di un sistema meccanico
- Teorema sulla variazione di quantità di moto
- Teorema sulla variazione del momento angolare
- Teorema del cambiamento di energia cinetica
- Forze agenti nelle macchine
- Forze in innesto di un ingranaggio cilindrico
- Attrito nei meccanismi e nelle macchine
- Attrito radente
- attrito volvente
- Efficienza
- Parti della macchina
- Trasmissioni meccaniche
- Tipi di ingranaggi meccanici
- Parametri base e derivati degli ingranaggi meccanici
- ingranaggi
- Ingranaggi con maglie flessibili
- Aste
- Scopo e classificazione
- Calcolo del progetto
- Verificare il calcolo degli alberi
- Cuscinetti
- Cuscinetti lisci
- Cuscinetti volventi
- Collegamento di parti della macchina
- Tipi di connessioni staccabili e permanenti
- Connessioni con chiave
- Trasmissioni meccaniche
- Standardizzazione delle norme, intercambiabilità
- Tolleranze e atterraggi
- Sistema unificato di tolleranze e atterraggi (ESDP)
- Deviazione di forma e posizione
Formato: pdf
Dimensioni: 4 MB
lingua russa
Un esempio del calcolo di un ingranaggio cilindrico
Un esempio del calcolo di un ingranaggio cilindrico. Sono stati effettuati la scelta del materiale, il calcolo delle sollecitazioni ammissibili, il calcolo della resistenza al contatto e alla flessione.
Un esempio di risoluzione del problema della flessione della trave
Nell'esempio vengono tracciati i diagrammi delle forze trasversali e dei momenti flettenti, viene trovata una sezione pericolosa e viene selezionata una trave a I. Nel problema è stata analizzata la costruzione di diagrammi utilizzando dipendenze differenziali, analisi comparativa diverse sezioni trasversali della trave.
Un esempio di risoluzione del problema della torsione dell'albero
Il compito è testare la resistenza di un albero in acciaio per un dato diametro, materiale e sollecitazioni consentite. Durante la soluzione, vengono costruiti i diagrammi delle coppie, delle sollecitazioni di taglio e degli angoli di torsione. Il peso proprio dell'albero non viene preso in considerazione
Un esempio di risoluzione del problema della tensione-compressione di un'asta
Il compito è testare la resistenza di una barra d'acciaio a determinate sollecitazioni ammissibili. Durante la soluzione vengono costruiti i grafici delle forze longitudinali, delle sollecitazioni normali e degli spostamenti. Il peso proprio della barra non viene preso in considerazione
Applicazione del teorema di conservazione dell'energia cinetica
Un esempio di risoluzione del problema dell'applicazione del teorema sulla conservazione dell'energia cinetica di un sistema meccanico
Determinazione della velocità e dell'accelerazione di un punto secondo le equazioni del moto date
Un esempio di risoluzione del problema di determinare la velocità e l'accelerazione di un punto secondo le equazioni del moto fornite
Determinazione delle velocità e delle accelerazioni dei punti di un corpo rigido durante il moto piano-parallelo
Un esempio di risoluzione del problema di determinare le velocità e le accelerazioni dei punti di un corpo rigido durante il movimento piano-parallelo
Determinazione delle forze nelle barre reticolari planari
Un esempio di risoluzione del problema della determinazione delle forze nelle barre di un traliccio piatto mediante il metodo Ritter e il metodo del taglio dei nodi
Come parte di qualsiasi curriculum, lo studio della fisica inizia con la meccanica. Non dalla teoria, non dall'applicazione e non dal calcolo, ma dalla buona vecchia meccanica classica. Questa meccanica è anche chiamata meccanica newtoniana. Secondo la leggenda, lo scienziato stava camminando in giardino, vide cadere una mela, e fu questo fenomeno che lo spinse a scoprire la legge della gravitazione universale. Certo, la legge è sempre esistita e Newton le ha dato solo una forma comprensibile alle persone, ma il suo merito non ha prezzo. In questo articolo non descriveremo le leggi della meccanica newtoniana nel modo più dettagliato possibile, ma delineeremo le basi, le conoscenze di base, le definizioni e le formule che possono sempre giocare nelle tue mani.
La meccanica è una branca della fisica, una scienza che studia il movimento dei corpi materiali e le interazioni tra di essi.
La parola stessa ha Origine greca e si traduce come "l'arte di costruire macchine". Ma prima di costruire macchine, abbiamo ancora molta strada da fare, quindi seguiamo le orme dei nostri antenati e studieremo il movimento delle pietre lanciate ad angolo rispetto all'orizzonte e le mele che cadono sulle teste da un'altezza h.

Perché lo studio della fisica inizia con la meccanica? Perché è del tutto naturale, non avviarlo dall'equilibrio termodinamico?!
La meccanica è una delle scienze più antiche, e storicamente lo studio della fisica è iniziato proprio con i fondamenti della meccanica. Poste nella cornice del tempo e dello spazio, le persone, infatti, non potevano partire da qualcos'altro, per quanto lo desiderassero. I corpi in movimento sono la prima cosa a cui prestiamo attenzione.
Cos'è il movimento?
Il movimento meccanico è un cambiamento nella posizione dei corpi nello spazio l'uno rispetto all'altro nel tempo.
È dopo questa definizione che arriviamo del tutto naturalmente al concetto di quadro di riferimento. Cambiare la posizione dei corpi nello spazio l'uno rispetto all'altro. Parole chiave qui: l'uno rispetto all'altro . Dopotutto, un passeggero in un'auto si muove rispetto a una persona in piedi sul ciglio della strada a una certa velocità, si riposa rispetto al suo vicino su un sedile vicino e si muove a un'altra velocità rispetto a un passeggero in un'auto che li sorpassa.

Ecco perché, per misurare normalmente i parametri degli oggetti in movimento e non confonderci, abbiamo bisogno sistema di riferimento - corpo di riferimento rigidamente interconnesso, sistema di coordinate e orologio. Ad esempio, la terra si muove intorno al sole in un sistema di riferimento eliocentrico. Nella vita di tutti i giorni, eseguiamo quasi tutte le nostre misurazioni in un sistema di riferimento geocentrico associato alla Terra. La terra è un corpo di riferimento rispetto al quale si muovono automobili, aerei, persone, animali.

La meccanica, come scienza, ha il suo compito. Il compito della meccanica è conoscere la posizione del corpo nello spazio in qualsiasi momento. In altre parole, la meccanica costruisce una descrizione matematica del moto e trova connessioni tra di loro quantità fisiche caratterizzandolo.
Per andare oltre, abbiamo bisogno della nozione di “ punto materiale ". Dicono che la fisica sia una scienza esatta, ma i fisici sanno quante approssimazioni e ipotesi devono essere fatte per concordare proprio questa accuratezza. Nessuno ha mai visto un punto materiale o annusato un gas ideale, ma esistono! È solo molto più facile conviverci.
Un punto materiale è un corpo le cui dimensioni e forma possono essere trascurate nel contesto di questo problema.
Sezioni di meccanica classica
La meccanica è composta da diverse sezioni
- Cinematica
- Dinamica
- Statica
Cinematica da un punto di vista fisico, studia esattamente come si muove il corpo. In altre parole, questa sezione si occupa delle caratteristiche quantitative del movimento. Trova velocità, percorso - compiti tipici della cinematica
Dinamica risolve la questione del perché si muove in quel modo. Cioè, considera le forze che agiscono sul corpo.
Statica studia l'equilibrio dei corpi sotto l'azione delle forze, cioè risponde alla domanda: perché non cade affatto?
Limiti di applicabilità della meccanica classica
La meccanica classica non pretende più di essere una scienza che spiega tutto (all'inizio del secolo scorso tutto era completamente diverso) e ha un chiaro ambito di applicabilità. In generale, le leggi della meccanica classica sono valide per il mondo a noi familiare in termini di dimensioni (macromondo). Smettono di funzionare nel caso del mondo delle particelle, quando la meccanica classica viene sostituita dalla meccanica quantistica. Inoltre, la meccanica classica non è applicabile ai casi in cui il movimento dei corpi avviene a una velocità prossima a quella della luce. In tali casi, gli effetti relativistici diventano pronunciati. In parole povere, nell'ambito della meccanica quantistica e relativistica - meccanica classica, questo è un caso speciale in cui le dimensioni del corpo sono grandi e la velocità è piccola.

In generale, gli effetti quantistici e relativistici non scompaiono mai; si verificano anche durante il normale movimento dei corpi macroscopici a una velocità molto inferiore a quella della luce. Un'altra cosa è che l'azione di questi effetti è così piccola che non va oltre il massimo misurazioni accurate. La meccanica classica non perderà dunque mai la sua fondamentale importanza.
Continueremo a studiare i fondamenti fisici della meccanica nei prossimi articoli. Per una migliore comprensione della meccanica, puoi sempre fare riferimento a nostri autori, che individualmente fanno luce sul punto oscuro del compito più difficile.
istituzione statale autonoma
Regione di Kaliningrad
organizzazione educativa professionale
Collegio dei Servizi e del Turismo
Corso di lezioni frontali con esempi di compiti pratici
"Fondamenti di Meccanica Teorica"
per disciplinaMeccanica tecnica
per studenti3 corso
specialità20.02.04 Sicurezza antincendio
Kaliningrad
APPROVARE
Vicedirettore per SD GAU KO VEO KSTN.N. Myasnikov
APPROVATO
Consiglio metodologico di GAU KO VET KST
CONSIDERATO
In una riunione del PCC
Gruppo editoriale:
Kolganova A.A., metodologa
Falaleeva A.B., insegnante di lingua e letteratura russa
Cvetaeva L.V., Presidente del PCCdiscipline generali della matematica e delle scienze naturali
Compilato da:
Nezvanov I.V. Docente GAU KO VET KST
Contenuto
Informazioni teoriche
Informazioni teoriche
Esempi di risoluzione di problemi pratici
Dinamica: concetti di base e assiomi
Informazioni teoriche
Esempi di risoluzione di problemi pratici
Bibliografia
Informazioni teoriche
Statica: concetti di base e assiomi.
Statica - una sezione di meccanica teorica, che considera le proprietà delle forze applicate ai punti di un corpo rigido, e le condizioni per il loro equilibrio. Obiettivi principali:
1. Trasformazione di sistemi di forze in sistemi di forze equivalenti.
2. Determinazione delle condizioni per l'equilibrio dei sistemi di forze agenti su un corpo rigido.
punto materiale chiamato il modello più semplice corpo materiale
qualsiasi forma, le cui dimensioni sono abbastanza piccole e che può essere presa come un punto geometrico avente una certa massa. Un sistema meccanico è qualsiasi insieme di punti materiali. Un corpo assolutamente rigido è un sistema meccanico, le cui distanze tra i punti non cambiano sotto nessuna interazione.
Forza è una misura dell'interazione meccanica dei corpi materiali tra loro. La forza è una grandezza vettoriale, poiché è determinata da tre elementi:
valore numerico;
direzione;
punto di applicazione (A).
L'unità di forza è Newton (N).

Figura 1.1
Un sistema di forze è un insieme di forze agenti su un corpo.
Un sistema di forze bilanciato (uguale a zero) è un sistema che, essendo applicato a un corpo, non ne cambia lo stato.
Il sistema di forze che agiscono sul corpo può essere sostituito da una risultante che agisce come sistema di forze.
Assiomi della statica.
Assioma 1: Se al corpo viene applicato un sistema equilibrato di forze, allora si muove in modo uniforme e rettilineo o è a riposo (legge di inerzia).
Assioma 2:
Un corpo assolutamente rigido è in equilibrio sotto l'azione di due forze se e solo se queste forze sono uguali in valore assoluto, agiscono lungo una linea retta e sono dirette in direzioni opposte. Figura 1.2
Assioma 3:
Lo stato meccanico del corpo non sarà disturbato se un sistema equilibrato di forze viene aggiunto o sottratto al sistema di forze che agiscono su di esso.
Assioma 4: La risultante delle due forze applicate al corpo è uguale alla loro somma geometrica, cioè è espressa in valore assoluto e direzione dalla diagonale del parallelogramma costruito su queste forze come sui lati.
Figura 1.3.
Assioma 5:
Le forze con cui due corpi agiscono l'uno sull'altro sono sempre uguali in valore assoluto e dirette lungo una retta in direzioni opposte.
Figura 1.4.
Tipi di legami e loro reazioni
connessioni
sono chiamate eventuali restrizioni che impediscono il movimento del corpo nello spazio. Il corpo, cercando sotto l'azione delle forze applicate di muoversi, che è impedito dalla connessione, agirà su di esso con una certa forza chiamata forza di pressione sulla connessione
. Secondo la legge dell'uguaglianza di azione e reazione, la connessione agirà sul corpo con lo stesso modulo, ma forza diretta in modo opposto.
Viene chiamata la forza con cui questa connessione agisce sul corpo, impedendo l'uno o l'altro movimento la forza di reazione (reazione) del legame
.
Uno dei principi fondamentali della meccanica è principio di liberazione
:
qualsiasi corpo non libero può essere considerato libero, se scartiamo i legami e sostituiamo la loro azione con le reazioni dei legami.
La reazione del legame è diretta nella direzione opposta a dove il legame non consente al corpo di muoversi. I principali tipi di legami e le loro reazioni sono mostrati nella Tabella 1.1.
Tabella 1.1
Tipi di legami e loro reazioni
Nome della comunicazione
Simbolo
1
Superficie liscia (supporto)
- la superficie (supporto), l'attrito su cui il dato corpo può essere trascurato.
Con il supporto gratuito, la reazioneè diretta perpendicolarmente alla tangente passante per il puntoMA
contatto corporeo1
con piano di appoggio2
.

2
Filo (flessibile, inestensibile). Il collegamento, realizzato sotto forma di un filo inestensibile, non consente al corpo di allontanarsi dal punto di sospensione. Pertanto, la reazione del filo è diretta lungo il filo fino al punto della sua sospensione.

3
asta senza peso
– una canna, il cui peso può essere trascurato rispetto al carico percepito.
La reazione di un'asta rettilinea incernierata senza peso è diretta lungo l'asse dell'asta.

4
Cerniera mobile, supporto mobile articolato. La reazione è diretta lungo la normale alla superficie di supporto.

7
Chiusura rigida.
Nel piano dell'incastonatura rigida ci saranno due componenti della reazione,
e momento di una coppia di forze, che impedisce la rotazione della trave1
relativo al puntoMA
.
Un attaccamento rigido nello spazio toglie tutti e sei i gradi di libertà dal corpo 1: tre spostamenti lungo gli assi coordinati e tre rotazioni attorno a questi assi.
Ci saranno tre componenti nell'incastonatura rigida spaziale,
,
e tre momenti di coppie di forze![]() .
.

Sistema di forze convergenti
Un sistema di forze convergenti
chiamato un sistema di forze le cui linee di azione si intersecano in un punto. Due forze che convergono in un punto, secondo il terzo assioma della statica, possono essere sostituite da una forza:risultante
.
Il vettore principale del sistema di forze
- un valore pari alla somma geometrica delle forze del sistema.
La risultante di un sistema piano di forze convergenti può essere definitograficamente e analiticamente.
Aggiunta di un sistema di forze . L'addizione di un sistema piano di forze convergenti viene effettuata o mediante addizione successiva di forze con la costruzione di una risultante intermedia (Fig. 1.5), oppure mediante la costruzione di un poligono di forza (Fig. 1.6).


Figura 1.5 Figura 1.6
Proiezione della forza sull'asse
- una grandezza algebrica pari al prodotto del modulo di forza per il coseno dell'angolo tra la forza e la direzione positiva dell'asse.
ProiezioneFX(fig.1.7) forze per asse Xpositivo se α è acuto, negativo se α è ottuso. Se forzaè perpendicolare all'asse, allora la sua proiezione sull'asse è nulla.

Figura 1.7
Proiezione della forza su un piano Oh– vettore , concluso tra le proiezioni dell'inizio e della fine della forzaa questo piano. Quelli. la proiezione della forza sul piano è una grandezza vettoriale, caratterizzata non solo da un valore numerico, ma anche dalla direzione nel pianoOh (figura 1.8).

Figura 1.8
Quindi il modulo di proiezione all'aereo Oh sarà uguale a:
Fxy = F cosα,
dove α è l'angolo tra le direzioni della forza e la sua proiezione.
Modo analitico di specificare le forze
.
Per il metodo analitico di impostazione della forzaè necessario scegliere un sistema di assi coordinatiOhz, in relazione al quale verrà determinata la direzione della forza nello spazio.
Un vettore che rappresenta la forza, può essere costruito se sono noti il modulo di questa forza e gli angoli α, β, γ che la forza forma con gli assi coordinati. PuntoMA applicazione della forza separatamente dalle sue coordinateX,
a,
z.z. Puoi impostare la forza dalle sue proiezionifx,
fy,
fzsugli assi coordinati. Il modulo di forza in questo caso è determinato dalla formula:
![]()
e coseni di direzione:
,
.
Metodo analitico di somma delle forze : la proiezione del vettore somma su un asse è uguale alla somma algebrica delle proiezioni dei termini dei vettori sullo stesso asse, cioè se:
poi , , .
Conoscere Rx, Ry, Rz, possiamo definire il modulo
![]()
e coseni di direzione:
, , .
Figura 1.9
Per l'equilibrio di un sistema di forze convergenti è necessario e sufficiente che la risultante di tali forze sia nulla.1) Condizione di equilibrio geometrico per un sistema convergente di forze : per l'equilibrio di un sistema di forze convergenti, è necessario e sufficiente che il poligono di forza costruito da queste forze
era chiuso (la fine del vettore dell'ultimo termine
forza deve coincidere con l'inizio del vettore del primo termine della forza). Quindi il vettore principale del sistema di forze sarà uguale a zero ()
2)
Condizioni di equilibrio analitico
.
Il modulo del vettore principale del sistema di forze è determinato dalla formula.
![]() =0. Perché il , allora l'espressione radice può essere uguale a zero solo se ogni termine svanisce simultaneamente, cioè
=0. Perché il , allora l'espressione radice può essere uguale a zero solo se ogni termine svanisce simultaneamente, cioè
Rx= 0, Ry= 0, R z = 0.
Pertanto, per l'equilibrio del sistema spaziale delle forze convergenti, è necessario e sufficiente che le somme delle proiezioni di tali forze su ciascuna delle tre coordinate degli assi siano uguali a zero:
Per l'equilibrio di un sistema piano di forze convergenti è necessario e sufficiente che la somma delle proiezioni delle forze su ciascuno dei due assi coordinati sia uguale a zero:
Somma di due forze parallele nella stessa direzione.

Figura 1.9
Due forze parallele dirette nella stessa direzione si riducono a una forza risultante parallela ad esse e diretta nella stessa direzione. La grandezza della risultante è uguale alla somma delle grandezze di queste forze, e il punto della sua applicazione C divide la distanza tra le linee di azione delle forze internamente in parti inversamente proporzionali alle grandezze di queste forze, cioèB A C
R=F 1 + F 2
La somma di due forze parallele disuguali dirette in direzioni opposte.
Due forze antiparallele disuguali si riducono ad una forza risultante parallela ad esse e diretta verso la forza maggiore. La grandezza della risultante è uguale alla differenza tra le grandezze di queste forze, e il punto della sua applicazione, C, divide la distanza tra le linee di azione delle forze esternamente in parti inversamente proporzionali alle grandezze di queste forze, che è
Coppia di forze e momento di forza rispetto a un punto.
Momento di forza
relativa al punto O si chiama, preso con l'apposito segno, il prodotto dell'intensità della forza per la distanza h dal punto O alla retta di azione della forza . Questo prodotto è preso con un segno più se la forza tende a ruotare il corpo in senso antiorario, e con il segno -, se la forza tende a ruotare il corpo in senso orario, cioè . Si chiama la lunghezza della perpendicolare hspalla di forza
punto O. L'effetto dell'azione della forza, ad es. l'accelerazione angolare del corpo è tanto maggiore quanto maggiore è l'entità del momento di forza.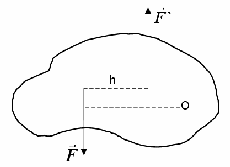
Figura 1.11
Un paio di forze Un sistema è chiamato un sistema costituito da due forze parallele di uguale intensità, dirette in direzioni opposte. Viene chiamata la distanza h tra le linee di azione delle forzecoppie di spalle . Momento di una coppia di forze m(F,F") è il prodotto del valore di una delle forze che compongono la coppia e del braccio della coppia, preso con l'apposito segno.Si scrive così: m(F, F")= ± F × h, dove il prodotto si prende con segno più se la coppia di forze tende a ruotare il corpo in senso antiorario e con segno meno se la coppia di forze tende per ruotare il corpo in senso orario.
Il teorema sulla somma dei momenti delle forze di una coppia.
La somma dei momenti delle forze della coppia (F,F") rispetto ad un qualsiasi punto 0 preso nel piano di azione della coppia non dipende dalla scelta di questo punto ed è pari al momento della coppia.
Teorema sulle coppie equivalenti. Conseguenze.
Teorema. Due coppie i cui momenti sono uguali tra loro sono equivalenti, cioè (FA, FA") ~ (FA, FA")
Corollario 1 . Una coppia di forze può essere trasferita in qualsiasi punto del piano della sua azione, nonché ruotata di qualsiasi angolo e modificare il braccio e l'entità delle forze della coppia, mantenendo il momento della coppia.
Conseguenza 2. Una coppia di forze non ha risultante e non può essere bilanciata da una forza che giace nel piano della coppia.

Figura 1.12
Addizione e condizioni di equilibrio per un sistema di coppie su un piano.
1. Teorema sull'addizione di coppie giacenti sullo stesso piano. Un sistema di coppie, situato arbitrariamente sullo stesso piano, può essere sostituito da una coppia, il cui momento è uguale alla somma dei momenti di queste coppie.
2. Teorema sull'equilibrio di un sistema di coppie su un piano.
Affinché un corpo assolutamente rigido sia in quiete sotto l'azione di un sistema di coppie, arbitrariamente disposte sullo stesso piano, è necessario e sufficiente che la somma dei momenti di tutte le coppie sia uguale a zero, cioè
Centro di gravità
Gravità - la risultante delle forze di attrazione verso la Terra, distribuite su tutto il volume del corpo.
Centro di gravità del corpo - questo è un tale punto, invariabilmente associato a questo corpo, attraverso il quale passa la linea di azione della forza di gravità di un dato corpo in qualsiasi posizione del corpo nello spazio.
Metodi per trovare il baricentro
1. Metodo di simmetria:
1.1. Se un corpo omogeneo ha un piano di simmetria, allora il centro di gravità giace su questo piano
1.2. Se un corpo omogeneo ha un asse di simmetria, allora il centro di gravità giace su questo asse. Il centro di gravità di un corpo di rivoluzione omogeneo giace sull'asse di rivoluzione.
1.3 Se un corpo omogeneo ha due assi di simmetria, allora il baricentro si trova nel punto della loro intersezione.
2. Metodo di partizione: Il corpo è diviso nel minor numero di parti, di cui sono note le forze di gravità e la posizione dei centri di gravità.
3. Metodo delle masse negative: quando si determina il baricentro di un corpo con cavità libere, dovrebbe essere utilizzato il metodo di partizione, ma la massa delle cavità libere dovrebbe essere considerata negativa.
Coordinate del baricentro di una figura piatta:

Le posizioni dei baricentri del semplice forme geometriche può essere calcolato utilizzando formule note. (Figura 1.13)

Nota: Il centro di gravità della simmetria della figura è sull'asse di simmetria.
Il centro di gravità dell'asta è a metà dell'altezza.
1.2. Esempi di risoluzione di problemi pratici
Esempio 1:
Un peso è sospeso su un'asta ed è in equilibrio. Determina le forze nella barra. (Figura 1.2.1)
Soluzione:
Le forze che sorgono nelle aste di fissaggio sono uguali in grandezza alle forze con cui le aste supportano il carico. (5° assioma)
Determiniamo le possibili direzioni delle reazioni dei legami "aste rigide".
Gli sforzi sono diretti lungo le aste.
Figura 1.2.1.
Liberiamo il punto A dai legami, sostituendo l'azione dei legami con le loro reazioni. (Figura 1.2.2)
Iniziamo la costruzione con una forza nota disegnando un vettoreFsu una certa scala.
Dalla fine del vettoreFtraccia linee parallele alle reazioniR 1 eR 2 .
Figura 1.2.2
Intersecando, le linee creano un triangolo. (Figura 1.2.3.). Conoscendo la scala delle costruzioni e misurando la lunghezza dei lati del triangolo, è possibile determinare l'entità delle reazioni nelle aste.
Per calcoli più accurati, puoi utilizzare le relazioni geometriche, in particolare il teorema del seno: il rapporto tra il lato del triangolo e il seno dell'angolo opposto è un valore costante
![]()
Per questo caso:
Figura 1.2.3
![]()
Commento: Se la direzione del vettore (reazione di accoppiamento) su un dato schema e nel triangolo delle forze non corrispondeva, allora la reazione sullo schema dovrebbe essere diretta nella direzione opposta.
Esempio 2:
Determinare l'intensità e la direzione del sistema piano risultante di forze convergenti in modo analitico.
Soluzione:
Figura 1.2.4
1. Determiniamo le proiezioni di tutte le forze del sistema su Ox (Figura 1.2.4)Sommando algebricamente le proiezioni si ottiene la proiezione della risultante sull'asse del bue.

Il segno indica che la risultante è diretta a sinistra.
2. Determiniamo le proiezioni di tutte le forze sull'asse Oy:
Sommando algebricamente le proiezioni, si ottiene la proiezione della risultante sull'asse Oy.
Il segno indica che la risultante è diretta verso il basso.
3. Determina il modulo della risultante in base alle grandezze delle proiezioni:
4. Determinare il valore dell'angolo della risultante con l'asse Ox:

e il valore dell'angolo con l'asse y:
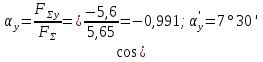
Esempio 3:
Calcolare la somma dei momenti delle forze relative al punto O (Figura 1.2.6).
O.A= AB= ARE=DE=DO=2m
Figura 1.2.6
Soluzione:
1. Il momento della forza relativo a un punto è numericamente uguale al prodotto del modulo e del braccio della forza.
2. Il momento della forza è uguale a zero se la linea di azione della forza passa per un punto.
Esempio 4:
Determinare la posizione del centro di gravità della figura mostrata nella Figura 1.2.7
Soluzione:
Dividiamo la figura in tre:
1-rettangolo
MA 1 =10*20=200 cm 2
2-triangolo
MA 2 =1/2*10*15=75 cm 2
3 giri
MA 3 =3,14*3 2 =28,3 cm 2
Figura 1 CG: x 1 =10 cm, a 1 =5 cm
Figura 2 CG: x 2 =20+1/3*15=25cm, u 2 =1/3*10=3,3 cm
Figura 3 CG: x 3 =10 cm, a 3 =5 cm
È definito in modo simile per Insieme a =4,5 cm
Cinematica: concetti base.
Parametri cinematici di base
Traiettoria - la linea che un punto materiale delinea quando si muove nello spazio. La traiettoria può essere una linea retta e una curva, una linea piatta e una spaziale.
Equazione della traiettoria per il moto piano: y =f ( X)
Distanza percorsa. Il percorso viene misurato lungo il percorso nella direzione di marcia. Designazione -S, unità di misura - metri.
Equazione del moto puntuale è un'equazione che determina la posizione di un punto in movimento in funzione del tempo.
Figura 2.1
La posizione di un punto in ogni istante di tempo può essere determinata dalla distanza percorsa lungo la traiettoria da un punto fisso, considerato come origine (Figura 2.1). Questo tipo di movimento è chiamatonaturale . Pertanto, l'equazione del moto può essere rappresentata come S = f (t).

Figura 2.2
La posizione di un punto può essere determinata anche se le sue coordinate sono note in funzione del tempo (Figura 2.2). Quindi, nel caso di moto su un piano, devono essere date due equazioni:Nel caso del moto spaziale si aggiunge anche una terza coordinataz.z= f 3 ( t)
Questo tipo di movimento è chiamatocoordinata .
Velocità di viaggio è una quantità vettoriale che caratterizza al momento la velocità e la direzione del movimento lungo la traiettoria.
La velocità è un vettore diretto in qualsiasi momento tangenzialmente alla traiettoria verso la direzione del moto (Figura 2.3).
Figura 2.3
Se un punto copre distanze uguali in intervalli di tempo uguali, viene chiamato il movimentouniforme .Velocità media sulla strada ΔSdefinito:
dove∆S- distanza percorsa nel tempo Δt; Δ t- Intervallo di tempo.
Se un punto percorre percorsi disuguali in intervalli di tempo uguali, viene chiamato il movimentoirregolare . In questo caso la velocità è una variabile e dipende dal tempov= f( t)
La velocità corrente è definita come
accelerazione puntiforme - una quantità vettoriale che caratterizza il tasso di variazione della velocità in grandezza e direzione.
La velocità di un punto quando ci si sposta dal punto M1 al punto Mg cambia in grandezza e direzione. Il valore medio dell'accelerazione per questo periodo di tempo
Accelerazione attuale:
Solitamente, per comodità, si considerano due componenti di accelerazione tra loro perpendicolari: normale e tangenziale (Figura 2.4)
Accelerazione normale a n , caratterizza il cambio di velocità di
direzione ed è definito come
L'accelerazione normale è sempre diretta perpendicolarmente alla velocità verso il centro dell'arco.
Figura 2.4
Accelerazione tangenziale a t , caratterizza il cambiamento di velocità in grandezza ed è sempre diretto tangenzialmente alla traiettoria; durante l'accelerazione, la sua direzione coincide con la direzione della velocità, e durante la decelerazione, è diretta opposta alla direzione del vettore velocità.![]()
Il valore di piena accelerazione è definito come:
Analisi delle tipologie e dei parametri cinematici dei movimenti
Movimento uniforme - Questo è un movimento a velocità costante:
Per moto rettilineo uniforme:
Per moto curvilineo uniforme:
![]()
Legge del moto uniforme :
Moto equa variabile – è un moto con accelerazione tangenziale costante:
Per moto rettilineo uniforme
Per moto curvilineo uniforme:
![]()
Legge del moto uniforme:
![]()
Grafici cinematici
Grafici cinematici - Questi sono grafici dei cambiamenti di percorso, velocità e accelerazione a seconda del tempo.
Movimento uniforme (Figura 2.5)

Figura 2.5
Movimento equa variabile (figura 2.6)

Figura 2.6
I moti più semplici di un corpo rigido
Movimento in avanti chiamato il movimento di un corpo rigido, in cui qualsiasi linea retta sul corpo durante il movimento rimane parallela alla sua posizione iniziale (Figura 2.7)

Figura 2.7
Nel moto traslatorio tutti i punti del corpo si muovono allo stesso modo: le velocità e le accelerazioni sono le stesse in ogni momento.
Inmoto rotatorio
tutti i punti del corpo descrivono cerchi attorno a un asse fisso comune.
Viene chiamato l'asse fisso attorno al quale ruotano tutti i punti del corpoasse di rotazione.
Per descrivere solo il moto rotatorio di un corpo attorno ad un asse fissoopzioni d'angolo. (Figura 2.8)
φ è l'angolo di rotazione del corpo;
ω – velocità angolare, determina la variazione dell'angolo di rotazione per unità di tempo;
La variazione della velocità angolare nel tempo è determinata dall'accelerazione angolare:
2.2. Esempi di risoluzione di problemi pratici
Esempio 1: L'equazione del moto di un punto è data. Determina la velocità del punto alla fine del terzo secondo di movimento e la velocità media per i primi tre secondi.
![]()
Soluzione:
1. Equazione della velocità
2. Velocità alla fine del terzo secondo (t=3 c)
3. Velocità media
Esempio 2: Secondo la data legge del moto, determina il tipo di moto, la velocità iniziale e l'accelerazione tangenziale del punto, il tempo per fermarsi.
![]()
Soluzione:
1. Tipo di movimento: ugualmente variabile (![]() )
)
2. Quando si confrontano le equazioni, è ovvio che
- il percorso iniziale percorso prima dell'inizio del conto alla rovescia 10m;
- velocità iniziale 20m/s
- accelerazione tangenziale costante ![]()
- l'accelerazione è negativa, quindi il movimento è lento, l'accelerazione è diretta nella direzione opposta alla velocità di movimento.
3. È possibile determinare il tempo in cui la velocità del punto sarà uguale a zero.
3. Dinamica: concetti di base e assiomi
Dinamica - una sezione di meccanica teorica in cui viene stabilita una connessione tra il movimento dei corpi e le forze che agiscono su di essi.
In dinamica, vengono risolti due tipi di problemi:
determinare i parametri di moto secondo le forze date;
determinare le forze che agiscono sul corpo, secondo i parametri cinematici del moto dati.
Sottopunto materiale
implica un certo corpo che ha una certa massa (cioè contiene una certa quantità di materia), ma non ha dimensioni lineari (un volume infinitesimale di spazio).
isolato
viene considerato un punto materiale, che non è influenzato da altri punti materiali. Nel mondo reale non esistono punti materiali isolati, così come corpi isolati, questo concetto è condizionale.
Con il moto traslatorio, tutti i punti del corpo si muovono allo stesso modo, quindi il corpo può essere considerato un punto materiale.
Se le dimensioni del corpo sono piccole rispetto alla traiettoria, può essere considerato anche un punto materiale, mentre il punto coincide con il baricentro del corpo.
Durante il movimento rotatorio del corpo, i punti potrebbero non muoversi allo stesso modo, in questo caso alcune disposizioni della dinamica possono essere applicate solo a singoli punti e l'oggetto materiale può essere considerato come un insieme di punti materiali.
Pertanto, la dinamica è divisa in dinamica di un punto e dinamica di un sistema materiale.
Assiomi della dinamica
Primo assioma ( principio di inerzia): in ogni punto materiale isolato è in uno stato di quiete o di moto uniforme e rettilineo finché le forze applicate non lo portano fuori da questo stato.
Questo stato è chiamato lo statoinerzia. Rimuovi il punto da questo stato, ad es. dagli un po' di accelerazione, forse una forza esterna.
Ogni corpo (punto) hainerzia. La misura dell'inerzia è la massa del corpo.
Messa chiamatola quantità di materia in un corpo in meccanica classica, è considerato un valore costante. L'unità di massa è il chilogrammo (kg).
Secondo assioma (La seconda legge di Newton è la legge fondamentale della dinamica)
F=ma
dovet - massa puntuale, kg;un - accelerazione puntuale, m/s 2 .
L'accelerazione impartita a un punto materiale da una forza è proporzionale all'intensità della forza e coincide con la direzione della forza.
La gravità agisce su tutti i corpi della Terra, imprime al corpo l'accelerazione della caduta libera, diretta verso il centro della Terra:
Sol=mg
doveg- 9,81 m/s², accelerazione in caduta libera.
Terzo assioma (Terza legge di Newton): conLe forze di interazione di due corpi sono uguali in grandezza e dirette lungo la stessa retta in direzioni diverse.
Quando interagiscono, le accelerazioni sono inversamente proporzionali alle masse.
Quarto assioma (legge di indipendenza dell'azione delle forze): aOgni forza del sistema di forze agisce come agirebbe da sola.
L'accelerazione impartita al punto dal sistema di forze è uguale alla somma geometrica delle accelerazioni impartite al punto da ciascuna forza separatamente (Figura 3.1):

Figura 3.1
Il concetto di attrito. Tipi di attrito.
Attrito-
resistenza derivante dal movimento di un corpo ruvido sulla superficie di un altro. L'attrito radente si traduce in attrito radente e l'attrito volvente provoca attrito oscillante.
Attrito radente
Figura 3.2.
Il motivo è l'impegno meccanico delle sporgenze. La forza di resistenza al movimento durante lo scorrimento è chiamata forza di attrito radente (Figura 3.2)Leggi dell'attrito radente:
1. La forza dell'attrito radente è direttamente proporzionale alla forza della pressione normale: 
doveR- forza di pressione normale, diretta perpendicolarmente al piano di appoggio;f- coefficiente di attrito radente.
Figura 3.3.
Nel caso di un corpo che si muove lungo un piano inclinato (Figura 3.3)attrito volvente
La resistenza al rotolamento è legata alla deformazione reciproca del terreno e della ruota ed è molto inferiore all'attrito radente.
Per un rotolamento uniforme della ruota, è necessario applicare forzaF dv (Figura 3.4)
La condizione di rotolamento della ruota è che il momento mobile non deve essere inferiore al momento di resistenza:
Figura 3.4.
Esempio 1: Esempio 2: A due punti materiali di massam 1 =2kg em 2 = 5 kg vengono applicate forze uguali. Confronta i valori più velocemente.Soluzione:
Secondo il terzo assioma, le dinamiche di accelerazione sono inversamente proporzionali alle masse: ![]()
Esempio 3:
Determinare il lavoro di gravità quando si sposta un carico dal punto A al punto C lungo un piano inclinato (Figura 3.7). La forza di gravità del corpo è 1500N. AB=6m, BC=4m. Esempio 3:
Determinare il lavoro della forza di taglio in 3 minuti. La velocità di rotazione del pezzo è di 120 giri/min, il diametro del pezzo è di 40 mm, la forza di taglio è di 1 kN. (Figura 3.8)
Soluzione:
1. Lavorare con moto rotatorio:
2. Velocità angolare 120 giri/min
Figura 3.8.
3. Il numero di giri per un dato tempo èz.z\u003d 120 * 3 \u003d 360 giri.Angolo di rotazione durante questo tempo φ=2πz.z\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Lavora per 3 turni:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Bibliografia
Olofinskaya, V.P. "Meccanica tecnica", "Forum" di Mosca 2011
Erdedi A.A. Erdedi N.A. Meccanica teorica. Resistenza dei materiali.- R-n-D; Fenice, 2010
1 diapositiva
Corso di lezioni su meccanica teorica Dinamica (I parte) Bondarenko A.N. Mosca - 2007 Il corso di formazione elettronica è stato scritto sulla base delle lezioni tenute dall'autore per gli studenti che studiano nelle specialità di SZhD, PGS e SDM presso NIIZhT e MIIT (1974-2006). Il materiale didattico corrisponde ai piani del calendario per un importo di tre semestri. Per implementare completamente gli effetti di animazione durante una presentazione, è necessario utilizzare un visualizzatore di Power Point non inferiore a Microsoft Office integrato sistema operativo Windows XP Professional. Commenti e suggerimenti possono essere inviati via e-mail: [e-mail protetta]. Università Statale di Mosca di Ingegneria Ferroviaria (MIIT) Dipartimento di Meccanica Teorica Centro Scientifico e Tecnico delle Tecnologie dei Trasporti

2 diapositiva
Contenuti Lezione 1. Introduzione alla dinamica. Leggi e assiomi della dinamica dei punti materiali. Equazione di base della dinamica. Equazioni differenziali e naturali del moto. Due compiti principali della dinamica. Esempi di risoluzione del problema diretto della dinamica Lezione 2. Risoluzione del problema inverso della dinamica. Istruzioni generali per risolvere il problema inverso della dinamica. Esempi di soluzione del problema inverso della dinamica. Il moto di un corpo lanciato ad angolo rispetto all'orizzonte, senza tener conto della resistenza dell'aria. Lezione 3. Oscillazioni rettilinee di un punto materiale. La condizione per il verificarsi di oscillazioni. Classificazione delle vibrazioni. Vibrazioni libere senza tener conto delle forze di resistenza. vibrazioni smorzate. Decremento dell'oscillazione. Lezione 4. Oscillazioni forzate di un punto materiale. Risonanza. Influenza della resistenza al movimento durante le vibrazioni forzate. Lezione 5. Moto relativo di un punto materiale. Forze di inerzia. Casi particolari di movimento per vari tipi di movimento portatile. Influenza della rotazione terrestre sull'equilibrio e sul moto dei corpi. Lezione 6. Dinamica di un sistema meccanico. sistema meccanico. Forze esterne ed interne. Centro di massa del sistema. Il teorema sul moto del centro di massa. Leggi di conservazione. Un esempio di risoluzione del problema dell'utilizzo del teorema sul movimento del centro di massa. Lezione 7. Impulso della forza. La quantità di movimento. Teorema sulla variazione di quantità di moto. Leggi di conservazione. Teorema di Eulero. Un esempio di risoluzione del problema sull'uso del teorema sulla variazione di quantità di moto. momento di slancio. Il teorema sulla variazione del momento angolare Lezione 8. Leggi di conservazione. Elementi di teoria dei momenti d'inerzia. Momento cinetico di un corpo rigido. Equazione differenziale della rotazione di un corpo rigido. Un esempio di risoluzione del problema dell'utilizzo del teorema sulla modifica del momento angolare del sistema. Teoria elementare del giroscopio. Letteratura consigliata 1. Yablonsky A.A. Corso di meccanica teorica. Parte 2. M.: Scuola superiore. 1977. 368 pag. 2. Meshchersky I.V. Raccolta di problemi di meccanica teorica. M.: Scienza. 1986 416 pag. 3. Raccolta di incarichi per tesine /Ed. AA. Yablonsky. M.: Scuola superiore. 1985. 366 pag. 4. Bondarenko A.n. “Meccanica teorica in esempi e compiti. Dynamics” (manuale elettronico www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 diapositiva
Lezione 1 Dinamica è una sezione di meccanica teorica che studia il moto meccanico dal punto di vista più generale. Il movimento è considerato in connessione con le forze che agiscono sull'oggetto. La sezione si compone di tre sezioni: Dinamica di un punto materiale Dinamica Dinamica di un sistema meccanico Meccanica analitica ■ Dinamica di un punto - studia il moto di un punto materiale, tenendo conto delle forze che causano questo movimento. L'oggetto principale è un punto materiale: un corpo materiale con una massa, le cui dimensioni possono essere trascurate. Assunzioni di base: - esiste uno spazio assoluto (ha proprietà puramente geometriche che non dipendono dalla materia e dal suo movimento. - esiste un tempo assoluto (non dipende dalla materia e dal suo movimento). Ne consegue: - esiste un sistema di riferimento assolutamente immobile - il tempo non dipende dal movimento del sistema di riferimento - le masse dei punti in movimento non dipendono dal movimento del sistema di riferimento Queste ipotesi sono utilizzate nella meccanica classica creata da Galileo e Newton Ha ancora una portata abbastanza ampia, poiché i sistemi meccanici considerati nelle scienze applicate non hanno masse e velocità di movimento così grandi, per le quali è necessario tener conto della loro influenza sulla geometria dello spazio, del tempo, del movimento, come è fatto nella meccanica relativistica (la teoria della relatività) ■ Le leggi fondamentali della dinamica - scoperte per la prima volta da Galileo e formulate da Newton costituiscono la base di tutti i metodi per descrivere e analizzare il movimento dei sistemi meccanici e la loro interazione dinamica azione sotto l'influenza di varie forze. ■ Legge di inerzia (legge di Galileo-Newton) - Un punto materiale isolato di un corpo mantiene il suo stato di quiete o di moto rettilineo uniforme finché le forze applicate non lo costringono a cambiare questo stato. Ciò implica l'equivalenza dello stato di quiete e moto per inerzia (la legge della relatività di Galileo). Il quadro di riferimento, in relazione al quale è soddisfatta la legge di inerzia, è chiamato inerziale. La proprietà di un punto materiale di sforzarsi di mantenere invariata la velocità del suo movimento (il suo stato cinematico) si chiama inerzia. ■ La legge di proporzionalità della forza e dell'accelerazione (Equazione di base della dinamica - II legge di Newton) - L'accelerazione impartita a un punto materiale dalla forza è direttamente proporzionale alla forza e inversamente proporzionale alla massa di questo punto: o Qui m è il massa del punto (una misura dell'inerzia), misurata in kg, numericamente uguale al peso diviso per l'accelerazione gravitazionale: F è la forza agente, misurata in N (1 N impartisce un'accelerazione di 1 m / s2 a un punto con un massa di 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Dinamica di un sistema meccanico - studia il movimento di un insieme di punti materiali e corpi rigidi, combinati leggi generali interazioni, tenendo conto delle forze che causano questo movimento. ■ Meccanica analitica - studia il moto di sistemi meccanici non liberi utilizzando metodi analitici generali. uno

4 diapositiva
Lezione 1 (segue - 1.2) Equazioni differenziali del moto di un punto materiale: - equazione differenziale del moto di un punto in forma vettoriale. - equazioni differenziali del moto puntuale in forma di coordinate. Questo risultato può essere ottenuto mediante proiezione formale dell'equazione differenziale vettoriale (1). Dopo il raggruppamento, la relazione del vettore viene scomposta in tre equazioni scalari: In forma di coordinate: usiamo la relazione del raggio-vettore con le coordinate e il vettore della forza con le proiezioni: equazione differenziale del moto sugli assi delle coordinate naturali (in movimento): o: - equazioni naturali del moto di un punto. ■ Equazione di base della dinamica: - corrisponde al modo vettoriale di specificare il movimento di un punto. ■ La legge di indipendenza dell'azione delle forze - L'accelerazione di un punto materiale sotto l'azione di più forze è uguale alla somma geometrica delle accelerazioni di un punto dall'azione di ciascuna delle forze separatamente: o La legge è valida per ogni stato cinematico dei corpi. Le forze di interazione, essendo applicate a diversi punti (corpi), non sono equilibrate. ■ La legge dell'uguaglianza di azione e reazione (III legge di Newton) - Ad ogni azione corrisponde una reazione uguale e contrariamente diretta: 2

5 diapositiva
Due problemi principali della dinamica: 1. Problema diretto: il moto è dato (equazioni del moto, traiettoria). È necessario determinare le forze sotto l'azione di cui si verifica un dato movimento. 2. Problema inverso: sono date le forze sotto l'azione delle quali avviene il movimento. È necessario trovare i parametri del moto (equazioni del moto, traiettoria del moto). Entrambi i problemi sono risolti utilizzando l'equazione di base della dinamica e la sua proiezione sugli assi coordinati. Se si considera il moto di un punto non libero, allora, come in statica, si usa il principio della liberazione dai vincoli. Come risultato della reazione, i legami sono inclusi nella composizione delle forze che agiscono sul punto materiale. La soluzione del primo problema è legata alle operazioni di derivazione. La soluzione del problema inverso richiede l'integrazione delle corrispondenti equazioni differenziali, e questo è molto più difficile della differenziazione. Il problema inverso è più difficile del problema diretto. La soluzione del problema diretto della dinamica - diamo un'occhiata agli esempi: Esempio 1. Una cabina con un peso G di un ascensore viene sollevata da un cavo con un'accelerazione a . Determinare la tensione del cavo. 1. Selezionare un oggetto (la cabina dell'ascensore si sposta in avanti e può essere considerata come un punto materiale). 2. Scartiamo la connessione (cavo) e la sostituiamo con la reazione R. 3. Compila l'equazione di base della dinamica: Determina la reazione del cavo: Determina la tensione del cavo: Con un movimento uniforme della cabina ay = 0 e il la tensione del cavo è uguale al peso: T = G. Quando il cavo si rompe T = 0 e l'accelerazione della cabina è uguale all'accelerazione di caduta libera: ay = -g. 3 4. Proiettiamo l'equazione di base della dinamica sull'asse y: y Esempio 2. Un punto di massa m si muove lungo una superficie orizzontale (il piano Oxy) secondo le equazioni: x = a coskt, y = b coskt. Determina la forza che agisce sul punto. 1. Selezionare un oggetto (punto materiale). 2. Scartiamo la connessione (piano) e la sostituiamo con la reazione N. 3. Aggiungiamo al sistema di forze una forza sconosciuta F. 4. Componi l'equazione di base della dinamica: 5. Proietta l'equazione di base della dinamica su assi x,y: Determinare le proiezioni della forza: Modulo di forza: Coseni di direzione: Pertanto, l'intensità della forza è proporzionale alla distanza del punto dal centro delle coordinate ed è diretta verso il centro lungo la linea che collega il punto al centro. La traiettoria del movimento del punto è un'ellisse centrata nell'origine: O r Lezione 1 (continua - 1.3)

6 scivolo
Lezione 1 (continuazione 1.4) Esempio 3: Un carico di peso G è sospeso su un cavo di lunghezza l e si muove lungo un percorso circolare su un piano orizzontale con una certa velocità. L'angolo di deviazione del cavo dalla verticale è uguale a. Determinare la tensione del cavo e la velocità del carico. 1. Seleziona un oggetto (carico). 2. Scartare la connessione (corda) e sostituirla con la reazione R. 3. Comporre l'equazione di base della dinamica: Dalla terza equazione, determinare la reazione del cavo: Determinare la tensione del cavo: Sostituire il valore della reazione del cavo, l'accelerazione normale nella seconda equazione e determinare la velocità del carico: 4. Proiettare l'equazione principale dinamica dell'asse,n,b: Esempio 4: Un'auto di peso G si muove su un ponte convesso (il raggio di curvatura è R ) con una velocità V. Determina la pressione dell'auto sul ponte. 1. Selezioniamo un oggetto (un'auto, trascuriamo le dimensioni e lo consideriamo come un punto). 2. Scartiamo la connessione (superficie ruvida) e la sostituiamo con le reazioni N e la forza di attrito Ffr. 3. Componiamo l'equazione di base della dinamica: 4. Proiettiamo l'equazione di base della dinamica sull'asse n: Da qui determiniamo la reazione normale: Determiniamo la pressione dell'auto sul ponte: Da qui possiamo determinare la velocità corrispondente a pressione nulla sul ponte (Q = 0): 4

7 scivolo
Lezione 2 Dopo aver sostituito i valori trovati delle costanti, otteniamo: Quindi, sotto l'azione dello stesso sistema di forze, un punto materiale può eseguire un'intera classe di movimenti determinati dalle condizioni iniziali. Le coordinate iniziali tengono conto della posizione iniziale del punto. La velocità iniziale, data dalle proiezioni, tiene conto dell'influenza sul suo movimento lungo la sezione considerata della traiettoria delle forze che hanno agito sul punto prima di arrivare a questa sezione, cioè stato cinematico iniziale. Soluzione del problema inverso della dinamica - Nel caso generale del movimento di un punto, le forze agenti sul punto sono variabili che dipendono dal tempo, dalle coordinate e dalla velocità. Il moto di un punto è descritto da un sistema di tre equazioni differenziali del secondo ordine: Dopo aver integrato ognuna di esse, si avranno sei costanti C1, C2,…., C6: I valori delle costanti C1, C2,… ., C6 si trovano da sei condizioni iniziali a t = 0: Esempio 1 della soluzione del problema inverso: Un punto materiale libero di massa m si muove sotto l'azione di una forza F, che è costante in grandezza e grandezza. . Al momento iniziale, la velocità del punto era v0 e coincideva in direzione con la forza. Determina l'equazione del moto di un punto. 1. Componi l'equazione di base della dinamica: 3. Abbassa l'ordine della derivata: 2. Scegli un sistema di riferimento cartesiano, orientando l'asse x lungo la direzione della forza e proietta l'equazione di base della dinamica su questo asse: o x y z 4 .Separare le variabili: 5. Calcolare gli integrali di entrambe le parti dell'equazione: 6. Rappresentiamo la proiezione della velocità come derivata della coordinata rispetto al tempo: 8. Calcolare gli integrali di entrambe le parti dell'equazione: 7. Separare le variabili: 9. Per determinare i valori delle costanti C1 e C2, utilizziamo le condizioni iniziali t = 0, vx = v0 , x = x0: Come risultato, otteniamo l'equazione del moto uniformemente variabile (lungo la asse x): 5

8 scivolo
Istruzioni generali per la risoluzione di problemi diretti e inversi. Procedura risolutiva: 1. Compilazione dell'equazione differenziale del moto: 1.1. Scegli un sistema di coordinate: rettangolare (fisso) con una traiettoria di movimento sconosciuta, naturale (in movimento) con una traiettoria nota, ad esempio un cerchio o una linea retta. In quest'ultimo caso, può essere utilizzata una coordinata rettilinea. Il punto di riferimento dovrebbe essere combinato con la posizione iniziale del punto (a t = 0) o con la posizione di equilibrio del punto, se esiste, ad esempio, quando il punto fluttua. 6 1.2. Disegna un punto in una posizione corrispondente a un momento arbitrario nel tempo (per t > 0) in modo che le coordinate siano positive (s > 0, x > 0). Assumiamo anche che anche la proiezione della velocità in questa posizione sia positiva. Nel caso delle oscillazioni, la proiezione della velocità cambia segno, per esempio, quando si ritorna alla posizione di equilibrio. Qui si dovrebbe presumere che nel momento considerato il punto si allontani dalla posizione di equilibrio. L'implementazione di questa raccomandazione è importante in futuro quando si lavora con forze di resistenza che dipendono dalla velocità. 1.3. Rilascia il punto materiale dai legami, sostituisci la loro azione con reazioni, aggiungi forze attive. 1.4. Scrivere la legge fondamentale della dinamica in forma vettoriale, proiettarla sugli assi selezionati, esprimere le forze date o reattive in termini di variabili tempo, coordinate o velocità, se dipendono da esse. 2. Soluzione di equazioni differenziali: 2.1. Ridurre la derivata se l'equazione non è ridotta alla forma canonica (standard). ad esempio: o 2.2. Variabili separate, ad esempio: o 2.4. Calcola non integrali definiti nelle parti sinistra e destra dell'equazione, ad esempio: 2.3. Se ci sono tre variabili nell'equazione, cambia le variabili, per esempio: e poi separa le variabili. Commento. Invece di calcolare integrali indefinitiè possibile calcolare integrali definiti con un limite superiore variabile. I limiti inferiori rappresentano i valori iniziali delle variabili (condizioni iniziali), quindi non è necessario trovare separatamente la costante, che viene automaticamente inclusa nella soluzione, ad esempio: Utilizzando le condizioni iniziali, ad esempio, t = 0 , vx = vx0, determinare la costante di integrazione: 2.5. Esprimere la velocità in termini di derivata temporale della coordinata, ad esempio, e ripetere i passaggi 2.2 -2.4 Nota. Se l'equazione viene ridotta a una forma canonica che ha una soluzione standard, viene utilizzata questa soluzione già pronta. Le costanti di integrazione si trovano ancora dalle condizioni iniziali. Vedi, ad esempio, le oscillazioni (lezione 4, p. 8). Lezione 2 (seguito 2.2)

9 diapositiva
Lezione 2 (continuazione 2.3) Esempio 2 di soluzione del problema inverso: La forza dipende dal tempo. Un carico di peso P inizia a muoversi lungo una superficie orizzontale liscia sotto l'azione di una forza F, la cui entità è proporzionale al tempo (F = kt). Determinare la distanza percorsa dal carico nel tempo t. 3. Componiamo l'equazione principale della dinamica: 5. Abbassiamo l'ordine della derivata: 4. Proiettiamo l'equazione principale della dinamica sull'asse x: o 7 6. Separiamo le variabili: 7. Calcoliamo gli integrali da entrambe le parti dell'equazione: 9. Rappresentiamo la proiezione della velocità come derivata della coordinata rispetto al tempo: 10. Calcola gli integrali di entrambe le parti dell'equazione: 9. Separa le variabili: 8. Determina il valore della costante C1 dalla condizione iniziale t = 0, vx = v0=0: Come risultato, si ottiene l'equazione del moto (lungo l'asse x), che dà il valore della distanza percorsa per il tempo t: 1. Si scegliamo il sistema di riferimento (coordinate cartesiane) in modo che il corpo abbia una coordinata positiva: 2. Prendiamo l'oggetto del moto come un punto materiale (il corpo si muove in avanti), lo liberiamo dalla connessione (piano di riferimento) e lo sostituiamo con il reazione (reazione normale di una superficie liscia) : 11. Determinare il valore della costante C2 dalla condizione iniziale t = 0, x = x0=0: Esempio 3 di soluzione del problema inverso: La forza dipende dalla coordinata. Un punto materiale di massa m viene lanciato verso l'alto dalla superficie terrestre con una velocità v0. La forza di gravità della Terra è inversamente proporzionale al quadrato della distanza dal punto al centro di gravità (il centro della Terra). Determina la dipendenza della velocità dalla distanza y dal centro della Terra. 1. Scegliamo un sistema di riferimento (coordinate cartesiane) in modo che il corpo abbia una coordinata positiva: 2. Componiamo l'equazione di base della dinamica: 3. Proiettiamo l'equazione di base della dinamica sull'asse y: oppure Il coefficiente di proporzionalità può essere trovato utilizzando il peso di un punto sulla superficie della Terra: R Quindi il differenziale l'equazione si presenta come: o 4. Diminuire l'ordine della derivata: 5. Cambiare la variabile: 6. Separare le variabili: 7. Calcolare il integrali di entrambi i lati dell'equazione: 8. Sostituisci i limiti: Di conseguenza, otteniamo un'espressione per la velocità in funzione della coordinata y: L'altezza massima del volo può essere trovata eguagliando la velocità a zero: La massima altitudine di volo quando il denominatore diventa zero: Da qui, impostando il raggio della Terra e l'accelerazione di caduta libera, si ottiene la II velocità cosmica:

10 diapositiva
Lezione 2 (continuazione 2.4) Esempio 2 di soluzione del problema inverso: La forza dipende dalla velocità. Una nave di massa m ha velocità v0. La resistenza dell'acqua al movimento della nave è proporzionale alla velocità. Determina il tempo necessario alla velocità della nave per dimezzarsi dopo aver spento il motore, nonché la distanza percorsa dalla nave fino all'arresto completo. 8 1. Scegliamo un sistema di riferimento (coordinate cartesiane) in modo che il corpo abbia una coordinata positiva: 2. Prendiamo l'oggetto del moto come un punto materiale (la nave si muove in avanti), lo liberiamo dai legami (acqua) e lo sostituiamo con una reazione (forza di galleggiamento - forza di Archimede), e anche la forza di resistenza al movimento. 3. Aggiungi forza attiva (gravità). 4. Componiamo l'equazione principale della dinamica: 5. Proiettiamo l'equazione principale della dinamica sull'asse x: oppure 6. Abbassiamo l'ordine della derivata: 7. Separiamo le variabili: 8. Calcoliamo gli integrali da entrambe le parti dell'equazione: 9. Sostituiamo i limiti: Si ottiene un'espressione che mette in relazione la velocità e il tempo t, da cui è possibile determinare il tempo di movimento: Il tempo di movimento, durante il quale la velocità diminuirà della metà: è interessante notare che quando la velocità si avvicina allo zero, il tempo di movimento tende all'infinito, cioè la velocità finale non può essere nulla. Perché non "moto perpetuo"? Tuttavia, in questo caso, la distanza percorsa fino alla fermata è un valore finito. Per determinare la distanza percorsa, ricorriamo all'espressione ottenuta dopo aver abbassato l'ordine della derivata, e facciamo un cambio di variabile: Dopo l'integrazione e la sostituzione dei limiti, otteniamo: Distanza percorsa fino all'arresto: ■ Movimento di un punto lanciato a un angolo rispetto all'orizzonte in un campo di gravità uniforme senza tener conto della resistenza dell'aria Eliminando il tempo dalle equazioni del moto, otteniamo l'equazione della traiettoria: Il tempo di volo è determinato equiparando la coordinata y a zero: L'autonomia di volo è determinata sostituendo il tempo di volo:

11 diapositiva
Lezione 3 Oscillazioni rettilinee di un punto materiale - Il movimento oscillatorio di un punto materiale avviene alla condizione: esiste una forza di ripristino che tende a riportare il punto nella posizione di equilibrio per qualsiasi deviazione da questa posizione. 9 C'è una forza di ripristino, la posizione di equilibrio è stabile Nessuna forza di ripristino, la posizione di equilibrio è instabile Nessuna forza di ripristino, la posizione di equilibrio è indifferente È sempre diretta verso la posizione di equilibrio, il valore è direttamente proporzionale all'allungamento lineare (accorciamento) della molla, che è pari allo scostamento del corpo dalla posizione di equilibrio: c è il coefficiente di rigidezza della molla, numericamente pari al forza sotto la quale la molla cambia la sua lunghezza di uno, misurata in N / m nel sistema SI. x y O Tipi di vibrazioni di un punto materiale: 1. Vibrazioni libere (senza tener conto della resistenza del mezzo). 2. Oscillazioni libere tenendo conto della resistenza del mezzo (oscillazioni smorzate). 3. Vibrazioni forzate. 4. Oscillazioni forzate che tengono conto della resistenza del mezzo. ■ Oscillazioni libere - si verificano solo sotto l'azione di una forza di ripristino. Scriviamo la legge fondamentale della dinamica: Scegliamo un sistema di coordinate centrato nella posizione di equilibrio (punto O) e proiettiamo l'equazione sull'asse x: Riportiamo l'equazione risultante nella forma standard (canonica): Questa equazione è un'equazione omogenea equazione differenziale lineare del secondo ordine, la cui forma della soluzione è determinata dalle radici della caratteristica dell'equazione ottenuta usando la sostituzione universale: le radici dell'equazione caratteristica sono immaginarie e uguali: la soluzione generale dell'equazione differenziale ha la forma: La velocità del punto: Condizioni iniziali: Definire le costanti: Quindi, l'equazione delle vibrazioni libere ha la forma: L'equazione può essere rappresentata da un'espressione a termine singolo: dove a è l'ampiezza, - fase iniziale. Le nuove costanti ae - sono legate alle costanti C1 e C2 dalle relazioni: Definiamo ae: La causa dell'occorrenza di oscillazioni libere è lo spostamento iniziale x0 e/o la velocità iniziale v0.

12 diapositiva
10 Lezione 3 (seguito 3.2) Oscillazioni smorzate di un punto materiale - Il movimento oscillatorio di un punto materiale avviene in presenza di una forza di ripristino e di una forza di resistenza al movimento. La dipendenza della forza di resistenza al movimento dallo spostamento o dalla velocità è determinata dalla natura fisica del mezzo o della connessione che impedisce il movimento. La dipendenza più semplice è una dipendenza lineare dalla velocità (resistenza viscosa): - coefficiente di viscosità x y O dai valori delle radici: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - caso di alta resistenza viscosa: - radici vere, diverse. oppure - queste funzioni sono aperiodiche: 3. n = k: - le radici sono reali, multiple. anche queste funzioni sono aperiodiche:

13 diapositiva
Lezione 3 (seguito 3.3) Classificazione delle soluzioni di oscillazioni libere. Connessioni a molla. durezza equivalente. si si 11 Diff. Carattere di equazione. Equazione Radici char. equazione Risoluzione dell'equazione differenziale Grafico nk n=k

14 diapositiva
Lezione 4 Vibrazioni forzate di un punto materiale - Insieme alla forza di ripristino, agisce una forza che cambia periodicamente, chiamata forza perturbante. La forza perturbante può avere natura diversa. Ad esempio, in un caso particolare, l'effetto inerziale di una massa sbilanciata m1 di un rotore rotante provoca proiezioni di forza che cambiano armonicamente: L'equazione principale della dinamica: La proiezione dell'equazione della dinamica sull'asse: Portiamo l'equazione allo standard forma: 12 La soluzione di questa equazione differenziale disomogenea consiste di due parti x = x1 + x2: x1 è la soluzione generale della corrispondente equazione omogenea e x2 è una soluzione particolare dell'equazione disomogenea: selezioniamo la soluzione particolare nella forma di lato destro: l'uguaglianza risultante deve essere soddisfatta per ogni t . Allora: o Così, con l'azione simultanea delle forze restitutrici e perturbatrici, il punto materiale compie un moto oscillatorio complesso, che è il risultato della somma (sovrapposizione) di vibrazioni libere (x1) e forzate (x2). Se pag< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (oscillazioni forzate ad alta frequenza), allora la fase delle oscillazioni è opposta alla fase della forza perturbatrice:

15 diapositiva
Lezione 4 (continuazione 4.2) 13 Coefficiente dinamico - il rapporto tra l'ampiezza delle oscillazioni forzate e la deviazione statica di un punto sotto l'azione di una forza costante H = const: L'ampiezza delle oscillazioni forzate: La deviazione statica può essere trovata dal equazione di equilibrio: Qui: Quindi: Quindi, a p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (alta frequenza delle oscillazioni forzate) coefficiente dinamico: Risonanza - si verifica quando la frequenza delle oscillazioni forzate coincide con la frequenza delle oscillazioni naturali (p = k). Ciò si verifica più spesso quando si avvia e si arresta la rotazione di rotori mal bilanciati montati su sospensioni elastiche. L'equazione differenziale delle oscillazioni con frequenze uguali: una soluzione particolare nella forma del membro destro non può essere presa, perché si otterrà una soluzione linearmente dipendente (vedi la soluzione generale). Soluzione generale: Sostituisci nell'equazione differenziale: Prendi una soluzione particolare nella forma e calcola le derivate: Così, la soluzione si ottiene: o Le oscillazioni forzate alla risonanza hanno un'ampiezza che aumenta indefinitamente in proporzione al tempo. Influenza della resistenza al movimento durante le vibrazioni forzate. L'equazione differenziale in presenza di resistenza viscosa ha la forma: La soluzione generale è selezionata dalla tabella (Lezione 3, p. 11) in base al rapporto tra n e k (vedi). Prendiamo una soluzione particolare nella forma e calcoliamo le derivate: Sostituisci nell'equazione differenziale: Uguagliando i coefficienti per funzioni trigonometriche identiche, otteniamo un sistema di equazioni: Elevando a potenza entrambe le equazioni e sommandole, otteniamo l'ampiezza della oscillazioni forzate: Dividendo la seconda equazione per la prima, si ottiene lo sfasamento delle oscillazioni forzate: Quindi , l'equazione del moto per le oscillazioni forzate, tenendo conto della resistenza al moto, per esempio, per n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 diapositiva
Lezione 5 Moto relativo di un punto materiale - Supponiamo che il sistema di coordinate mobili (non inerziali) Oxyz si muova secondo qualche legge relativa al sistema di coordinate fisse (inerziali) O1x1y1z1. Il moto di un punto materiale M (x, y, z) rispetto al sistema mobile Oxyz è relativo, rispetto al sistema immobile O1x1y1z1 è assoluto. Il moto del sistema mobile Oxyz relativo al sistema fisso O1x1y1z1 è un moto portatile. 14 z x1 y1 z1 O1 x y M x y z O Equazione di base della dinamica: Accelerazione assoluta di un punto: Sostituisci l'accelerazione assoluta di un punto nell'equazione di base della dinamica: Trasferiamo i termini con traslazione e accelerazione di Coriolis a destra: Il i termini trasferiti hanno la dimensione delle forze e sono considerati come le corrispondenti forze inerziali, uguali: Allora il moto relativo di un punto può essere considerato assoluto, se alle forze agenti si sommano le forze traslazionali e di Coriolis d'inerzia: Nelle proiezioni sulla assi del sistema di coordinate mobili, abbiamo: diverso tipo moto traslatorio: 1. Rotazione attorno ad un asse fisso: Se la rotazione è uniforme, allora εe = 0: 2. Moto curvilineo traslatorio: Se il moto è rettilineo, allora = : Se il moto è rettilineo e uniforme, allora il sistema in moto è il moto inerziale e relativo può essere considerato assoluto: nessun fenomeno meccanico può rilevare un moto rettilineo uniforme (principio di relatività della meccanica classica). Influenza della rotazione terrestre sull'equilibrio dei corpi - Supponiamo che il corpo sia in equilibrio sulla superficie terrestre ad una latitudine arbitraria φ (parallele). La Terra ruota attorno al proprio asse da ovest a est con una velocità angolare: il raggio della Terra è di circa 6370 km. SR è la reazione totale di una superficie non liscia. G - forza di attrazione della Terra verso il centro. Ф - forza centrifuga di inerzia. Condizione di equilibrio relativo: La risultante delle forze di attrazione e di inerzia è la forza di gravità (peso): L'entità della forza di gravità (peso) sulla superficie della Terra è P = mg. La forza centrifuga di inerzia è una piccola frazione della forza di gravità: anche la deviazione della forza di gravità dalla direzione della forza di attrazione è piccola: quindi, l'influenza della rotazione terrestre sull'equilibrio dei corpi è estremamente piccola e non viene preso in considerazione nei calcoli pratici. Il valore massimo della forza inerziale (a φ = 0 - all'equatore) è solo 0,00343 del valore della gravità

17 diapositiva
Lezione 5 (continuazione 5.2) 15 Influenza della rotazione terrestre sul movimento dei corpi nel campo gravitazionale terrestre - Supponiamo che un corpo cada sulla Terra da una certa altezza H sopra la superficie terrestre alla latitudine φ . Scegliamo un sistema di riferimento mobile, rigidamente connesso con la Terra, orientando gli assi x, y tangenzialmente al parallelo e al meridiano: Equazione del moto relativo: qui si tiene conto della piccolezza della forza centrifuga di inerzia rispetto alla gravità . Pertanto, la forza di gravità è identificata con la forza di gravità. Inoltre, assumiamo che la gravità sia diretta perpendicolarmente alla superficie terrestre a causa della piccolezza della sua deflessione, come discusso sopra. L'accelerazione di Coriolis è uguale e diretta parallelamente all'asse y verso ovest. La forza di inerzia di Coriolis è diretta nella direzione opposta. Proiettiamo sull'asse l'equazione del moto relativo: La soluzione della prima equazione dà: Condizioni iniziali: La soluzione della terza equazione dà: Condizioni iniziali: La terza equazione assume la forma: Condizioni iniziali: La sua soluzione dà: La soluzione risultante mostra che il corpo devia verso est quando cade. Calcoliamo il valore di questa deviazione, ad esempio, quando cadiamo da un'altezza di 100 m Troviamo il tempo di caduta dalla soluzione della seconda equazione: Pertanto, l'influenza della rotazione terrestre sul movimento dei corpi è estremamente ridotta per altezze e velocità pratiche e non viene preso in considerazione nei calcoli tecnici. La soluzione della seconda equazione implica anche l'esistenza di una velocità lungo l'asse y, che dovrebbe anche causare e causa la corrispondente accelerazione e la forza di inerzia di Coriolis. L'influenza di questa velocità e della forza d'inerzia ad essa associata sulla variazione del moto sarà ancora minore della forza d'inerzia di Coriolis considerata associata alla velocità verticale.

18 diapositiva
Lezione 6 Dinamica di un sistema meccanico. Sistema di punti materiali o sistema meccanico - Un insieme di punti materiali o quei punti materiali uniti da leggi generali di interazione (la posizione o il movimento di ciascuno dei punti o di un corpo dipende dalla posizione e dal movimento di tutti gli altri) Il sistema di punti liberi - il cui movimento non è limitato da alcuna connessione (ad esempio, un sistema planetario , in cui i pianeti sono considerati punti materiali). Un sistema di punti non liberi o un sistema meccanico non libero: il movimento di punti o corpi materiali è limitato dai vincoli imposti al sistema (ad esempio, un meccanismo, una macchina, ecc.). 16 Forze agenti sul sistema. Oltre alla classificazione delle forze precedentemente esistente (forze attive e reattive), viene introdotta una nuova classificazione delle forze: 1. Forze esterne (e) - agenti su punti e corpi del sistema da punti o corpi che non ne fanno parte sistema. 2. Forze interne (i) - forze di interazione tra punti o corpi materiali inclusi nel sistema dato. La stessa forza può essere sia esterna che interna. Tutto dipende da quale sistema meccanico è considerato. Ad esempio: nel sistema del Sole, della Terra e della Luna, tutte le forze gravitazionali tra di loro sono interne. Considerando il sistema Terra e Luna, le forze gravitazionali applicate dal lato del Sole sono esterne: C Z L In base alla legge di azione e reazione, ad ogni forza interna Fk corrisponde un'altra forza interna Fk', uguale in valore assoluto e opposta in direzione. Da questo ne seguono due proprietà meravigliose forze interne: il vettore principale di tutte le forze interne del sistema è zero: il momento principale di tutte le forze interne del sistema relativo a qualsiasi centro è zero: o nelle proiezioni sugli assi delle coordinate: Nota. Sebbene queste equazioni siano simili alle equazioni di equilibrio, non lo sono, poiché le forze interne sono applicate a vari punti o corpi del sistema e possono far muovere questi punti (corpi) l'uno rispetto all'altro. Da queste equazioni risulta che le forze interne non influenzano il moto di un sistema considerato nel suo insieme. Il centro di massa del sistema di punti materiali. Per descrivere il movimento del sistema nel suo insieme, viene introdotto un punto geometrico, chiamato centro di massa, il cui raggio vettore è determinato dall'espressione, dove M è la massa dell'intero sistema: O in proiezioni sulla coordinata assi: Le formule per il centro di massa sono simili a quelle per il centro di gravità. Tuttavia, il concetto di centro di massa è più generale, poiché non è correlato alle forze di gravità o alle forze di gravità.

19 diapositiva
Lezione 6 (seguito 6.2) 17 Teorema sul moto del centro di massa del sistema - Si consideri un sistema di n punti materiali. Dividiamo le forze applicate a ciascun punto in esterne e interne e le sostituiamo con le corrispondenti risultanti Fke e Fki. Scriviamo per ogni punto l'equazione di base della dinamica: oppure Sommiamo queste equazioni su tutti i punti: Sul lato sinistro dell'equazione, introdurremo le masse sotto il segno della derivata e sostituiremo la somma delle derivate con la derivata della somma: Dalla definizione del centro di massa: Sostituisci nell'equazione risultante: otteniamo o: Il prodotto della massa del sistema e l'accelerazione della sua massa centrale è uguale al vettore principale delle forze esterne. Nelle proiezioni sugli assi coordinati: il centro di massa del sistema si sposta come un punto materiale con una massa uguale alla massa dell'intero sistema, a cui vengono applicate tutte le forze esterne che agiscono sul sistema. Conseguenze dal teorema sul moto del centro di massa del sistema (leggi di conservazione): 1. Se nell'intervallo di tempo il vettore principale delle forze esterne del sistema è uguale a zero, Re = 0, allora la velocità di il centro di massa è costante, vC = const (il centro di massa si muove uniformemente in modo rettilineo - la legge di conservazione del moto centro di massa). 2. Se nell'intervallo di tempo la proiezione del vettore principale delle forze esterne del sistema sull'asse x è uguale a zero, Rxe = 0, allora la velocità del centro di massa lungo l'asse x è costante, vCx = const (il centro di massa si sposta uniformemente lungo l'asse). Dichiarazioni simili sono vere per gli assi y e z. Esempio: due persone di massa m1 e m2 si trovano su una barca di massa m3. Al momento iniziale, la barca con le persone era ferma. Determina lo spostamento della barca se una persona di massa m2 si sposta a prua della barca a una distanza a. 3. Se nell'intervallo di tempo il vettore principale delle forze esterne del sistema è uguale a zero, Re = 0, e al momento iniziale la velocità del centro di massa è uguale a zero, vC = 0, allora il raggio vettore del centro di massa rimane costante, rC = const (il centro di massa è a riposo è la legge di conservazione della posizione del centro di massa). 4. Se nell'intervallo di tempo la proiezione del vettore principale delle forze esterne del sistema sull'asse x è uguale a zero, Rxe = 0, e al momento iniziale la velocità del centro di massa lungo questo asse è zero , vCx = 0, allora la coordinata del centro di massa lungo l'asse x rimane costante, xC = const (il centro di massa non si sposta lungo questo asse). Dichiarazioni simili sono vere per gli assi y e z. 1. Oggetto del movimento (barca con persone): 2. Eliminare le connessioni (acqua): 3. Sostituire la connessione con la reazione: 4. Aggiungere le forze attive: 5. Annotare il teorema sul centro di massa: Proiettare sull'asse x : O Determina quanto devi trasferire a una persona di massa m1, in modo che la barca rimanga in posizione: la barca si sposterà di una distanza l nella direzione opposta.

20 diapositive
Lezione 7 L'impulso di forza è una misura dell'interazione meccanica che caratterizza il trasferimento del moto meccanico delle forze agenti sul punto per un dato periodo di tempo: 18 In proiezioni sugli assi coordinati: Nel caso di forza costante: In proiezioni sugli assi delle coordinate: al punto di forza nello stesso intervallo di tempo: Moltiplicare per dt: Integrare su un dato intervallo di tempo: La quantità di movimento del punto è una misura del movimento meccanico, determinata da un vettore uguale al prodotto di la massa del punto e il vettore della sua velocità: Teorema sulla variazione dell'entità del movimento del sistema – Si consideri il sistema n punti materiali. Dividiamo le forze applicate a ciascun punto in esterne e interne e le sostituiamo con le corrispondenti risultanti Fke e Fki. Scriviamo per ogni punto l'equazione di base della dinamica: o La quantità di moto del sistema di punti materiali è la somma geometrica delle quantità di moto dei punti materiali: Per definizione del centro di massa: Il vettore della quantità di moto del sistema è uguale al prodotto della massa dell'intero sistema e del vettore velocità del centro di massa del sistema. Quindi: Nelle proiezioni sugli assi coordinati: La derivata temporale del vettore momento del sistema è uguale al vettore principale delle forze esterne del sistema. Sommiamo queste equazioni su tutti i punti: Sul lato sinistro dell'equazione, introduciamo le masse sotto il segno della derivata e sostituiamo la somma delle derivate con la derivata della somma: Dalla definizione della quantità di moto del sistema: Nelle proiezioni sugli assi delle coordinate:

21 diapositiva
Teorema di Eulero - Applicazione del teorema sulla variazione della quantità di moto di un sistema al moto di un mezzo continuo (acqua). 1. Selezioniamo come oggetto di movimento il volume d'acqua situato nel canale curvilineo della turbina: 2. Scartiamo i legami e sostituiamo la loro azione con reazioni (Rpov - la risultante delle forze superficiali) 3. Aggiungiamo le forze attive (Rb - la risultante delle forze del corpo): 4. Annotare il teorema sulla variazione della quantità di moto del sistema: La quantità di moto dell'acqua agli istanti t0 e t1 è rappresentata come somme: Variazione della quantità di moto dell'acqua nell'intervallo di tempo : Variazione di la quantità di moto dell'acqua in un intervallo di tempo infinitesimale dt: , dove F1 F2 Facendo il prodotto della densità, dell'area della sezione trasversale e della velocità per secondo di massa, si ottiene: Sostituendo il differenziale della quantità di moto del sistema nel teorema di cambiamento, si ottiene : Conseguenze dal teorema sulla variazione della quantità di moto del sistema (leggi di conservazione): 1. Se nell'intervallo di tempo il vettore principale delle forze esterne del sistema è uguale a zero, Re = 0, allora il moto del vettore quantità è costante, Q = const è la legge di conservazione della quantità di moto del sistema). 2. Se nell'intervallo di tempo la proiezione del vettore principale delle forze esterne del sistema sull'asse x è uguale a zero, Rxe = 0, allora la proiezione della quantità di moto del sistema sull'asse x è costante, Qx = cost. Dichiarazioni simili sono vere per gli assi y e z. Lezione 7 (continuazione di 7.2) Esempio: Una granata di massa M, volando a velocità v, è esplosa in due parti. La velocità di uno dei frammenti di massa m1 è aumentata nella direzione del moto fino al valore v1. Determina la velocità del secondo frammento. 1. L'oggetto del movimento (granata): 2. L'oggetto è un sistema libero, non ci sono connessioni e le loro reazioni. 3. Somma delle forze attive: 4. Annota il teorema sulla variazione di momento: Proietta sull'asse: β Dividi le variabili e integra: L'integrale retto è quasi nullo, perché tempo di esplosione t

22 diapositiva
Lezione 7 (continuazione 7.3) 20 Il momento angolare di un punto o momento cinetico del moto relativo a un certo centro è una misura del moto meccanico, determinata da un vettore uguale al prodotto vettoriale del raggio vettore di un punto materiale per il vettore della sua quantità di moto: Il momento cinetico di un sistema di punti materiali rispetto a un certo centro è geometrico la somma dei momenti della quantità di moto di tutti i punti materiali relativi allo stesso centro: In proiezioni sull'asse: In proiezioni sull'asse : Teorema sulla variazione del momento d'impulso del sistema - Consideriamo un sistema di n punti materiali. Dividiamo le forze applicate a ciascun punto in esterne e interne e le sostituiamo con le corrispondenti risultanti Fke e Fki. Scriviamo per ogni punto l'equazione di base della dinamica: oppure Sommiamo queste equazioni su tutti i punti: Sostituiamo la somma delle derivate con la derivata della somma: L'espressione tra parentesi è il momento della quantità di moto del sistema. Da qui: Moltiplichiamo vettorialmente ciascuna delle uguaglianze per il raggio-vettore a sinistra: Vediamo se è possibile portare il segno della derivata oltre i limiti del prodotto vettoriale: Quindi, abbiamo: centro. Nelle proiezioni sugli assi coordinati: La derivata del momento di quantità di moto del sistema rispetto a qualche asse nel tempo è uguale al momento principale delle forze esterne del sistema rispetto allo stesso asse.

23 diapositiva
Lezione 8 21 ■ Conseguenze del teorema sulla variazione del momento angolare del sistema (leggi di conservazione): 1. Se nell'intervallo di tempo il vettore del momento principale delle forze esterne del sistema rispetto a un certo centro è uguale a zero, MOe = 0, allora il vettore del momento angolare del sistema relativo al centro stesso è costante, KO = const è la legge di conservazione della quantità di moto del sistema). 2. Se nell'intervallo di tempo il momento principale delle forze esterne del sistema rispetto all'asse x è uguale a zero, Mxe = 0, allora il momento angolare del sistema rispetto all'asse x è costante, Kx = const. Dichiarazioni simili sono vere per gli assi y e z. 2. Momento di inerzia di un corpo rigido attorno a un asse: Il momento di inerzia di un punto materiale attorno a un asse è uguale al prodotto della massa del punto e al quadrato della distanza del punto dall'asse. Il momento d'inerzia di un corpo rigido attorno ad un asse è uguale alla somma dei prodotti della massa di ciascun punto per il quadrato della distanza di questo punto dall'asse. ■ Elementi di teoria dei momenti d'inerzia - Nel moto rotatorio di un corpo rigido, la misura dell'inerzia (resistenza alla variazione del moto) è il momento d'inerzia attorno all'asse di rotazione. Considera i concetti di base della definizione e dei metodi per il calcolo dei momenti di inerzia. 1. Momento di inerzia di un punto materiale attorno all'asse: nella transizione da una piccola massa discreta a una massa infinitamente piccola di un punto, il limite di tale somma è determinato dall'integrale: momento di inerzia assiale di un corpo rigido . Oltre al momento d'inerzia assiale di un corpo rigido, esistono altri tipi di momenti d'inerzia: il momento d'inerzia centrifugo di un corpo rigido. Momento polare d'inerzia di un corpo rigido. 3. Il teorema sui momenti di inerzia di un corpo rigido rispetto ad assi paralleli - la formula per il passaggio ad assi paralleli: Momento di inerzia rispetto all'asse di riferimento Momenti statici di inerzia rispetto agli assi di riferimento I momenti di massa corporea sono pari a zero:

24 diapositiva
Lezione 8 (continuazione 8.2) 22 Momento di inerzia di un'asta uniforme di sezione costante attorno all'asse: x z L Selezionare il volume elementare dV = Adx alla distanza x: x dx Massa elementare: Per calcolare il momento di inerzia attorno all'asse centrale (passante per il baricentro), è sufficiente cambiare la posizione dell'asse e impostare i limiti di integrazione (-L/2, L/2). Qui dimostriamo la formula per la transizione ad assi paralleli: zС 5. Il momento di inerzia di un cilindro solido omogeneo attorno all'asse di simmetria: H dr r Individuiamo il volume elementare dV = 2πrdrH (cilindro sottile di raggio r) : Massa elementare: qui usiamo la formula del volume del cilindro V=πR2H. Per calcolare il momento di inerzia di un cilindro cavo (spesso), è sufficiente impostare i limiti di integrazione da R1 a R2 (R2> R1): 6. Il momento di inerzia di un cilindro sottile attorno all'asse di simmetria (t

25 diapositiva
Lezione 8 (continuazione 8.3) 23 ■ Equazione differenziale della rotazione di un corpo rigido attorno a un asse: Scriviamo un teorema sulla modifica del momento angolare di un corpo rigido che ruota intorno a un asse fisso: Il momento di un corpo rigido in rotazione è: Il momento delle forze esterne attorno all'asse di rotazione è uguale alla coppia (reazioni e forze non creano momenti gravitazionali): Sostituiamo il momento cinetico e la coppia nel teorema Esempio: Due persone dello stesso peso G1 = G2 sono appese a una corda gettato su un blocco solido con un peso G3 = G1/4. Ad un certo punto, uno di loro ha iniziato a salire sulla corda con una velocità relativa u. Determina la velocità di sollevamento di ogni persona. 1. Selezioniamo l'oggetto del movimento (blocco con persone): 2. Scartiamo le connessioni (il dispositivo di supporto del blocco): 3. Sostituiamo la connessione con reazioni (cuscinetto): 4. Aggiungi forze attive (gravità): 5. Annotare il teorema sulla variazione del momento cinetico del sistema rispetto all'asse di rotazione del blocco: R Poiché il momento delle forze esterne è uguale a zero, il momento cinetico deve rimanere costante: All'istante iniziale t = 0, c'era equilibrio e Kz0 = 0. Dopo l'inizio del movimento di una persona rispetto alla fune, l'intero sistema ha iniziato a muoversi, ma il momento cinetico del sistema deve rimanere uguale a zero: Kz = 0. Il momento angolare del sistema è la somma dei momenti angolari di entrambe le persone e del blocco: qui v2 è la velocità della seconda persona, uguale alla velocità dell'estremità del cavo rispetto a un asse di rotazione fisso. Oppure: In caso di piccole oscillazioni sinφ φ: Periodo di oscillazione: Momento di inerzia della barra:

26 diapositiva
Lezione 8 (continuazione 8.4 - materiale aggiuntivo) 24 ■ Teoria elementare del giroscopio: Un giroscopio è un corpo rigido che ruota attorno all'asse di simmetria materiale, uno dei cui punti è fisso. Un giroscopio libero è fissato in modo tale che il suo centro di massa rimanga fermo e l'asse di rotazione passi attraverso il centro di massa e possa assumere qualsiasi posizione nello spazio, ad es. l'asse di rotazione cambia la sua posizione come l'asse di rotazione del corpo stesso durante il movimento sferico. L'assunto principale della teoria approssimativa (elementare) del giroscopio è che il vettore del momento (momento cinetico) del rotore sia considerato diretto lungo il proprio asse di rotazione. Pertanto, nonostante il fatto che nel caso generale il rotore partecipi a tre rotazioni, viene presa in considerazione solo la velocità angolare della propria rotazione ω = dφ/dt. La ragione di ciò è che nella tecnologia moderna il rotore del giroscopio ruota con una velocità angolare dell'ordine di 5000-8000 rad / s (circa 50000-80000 rpm), mentre le altre due velocità angolari associate alla precessione e alla nutazione del proprio asse di rotazione decine di migliaia di volte inferiore a questa velocità. La proprietà principale di un giroscopio libero è che l'asse del rotore mantiene una direzione costante nello spazio rispetto al sistema di riferimento inerziale (stellare) (dimostrato dal pendolo di Foucault, che mantiene invariato il piano oscillante rispetto alle stelle, 1852). Ciò deriva dalla legge di conservazione del momento cinetico relativo al centro di massa del rotore, a condizione che l'attrito nei cuscinetti degli assi della sospensione del rotore, il telaio esterno e interno sia trascurato: Azione della forza sull'asse di un libero giroscopio. Nel caso di una forza applicata all'asse del rotore, il momento delle forze esterne rispetto al centro di massa non è uguale a zero: ω ω С forza, e verso il vettore del momento di questa forza, cioè ruoterà non attorno all'asse x (sospensione interna), ma attorno all'asse y (sospensione esterna). Al termine della forza, l'asse del rotore rimarrà nella stessa posizione, corrispondente all'ultimo tempo della forza, perché da questo punto nel tempo, il momento delle forze esterne diventa nuovamente uguale a zero. Nel caso di un'azione di forza a breve termine (impatto), l'asse del giroscopio praticamente non cambia posizione. Pertanto, la rapida rotazione del rotore conferisce al giroscopio la capacità di contrastare le influenze casuali che cercano di modificare la posizione dell'asse di rotazione del rotore e, con un'azione costante della forza, mantiene la posizione del piano perpendicolare a la forza agente in cui giace l'asse del rotore. Queste proprietà sono utilizzate nel funzionamento dei sistemi di navigazione inerziale.
Lezioni di Meccanica Teorica
Dinamica puntuale
Lezione 1
Concetti di base della dinamica
Nel cap Dinamica si studia il movimento dei corpi sotto l'azione delle forze ad essi applicate. Pertanto, oltre a quei concetti che sono stati introdotti nell'art Cinematica, qui è necessario utilizzare nuovi concetti che riflettano le specificità dell'impatto delle forze su vari corpi e la risposta dei corpi a questi impatti. Consideriamo il principale di questi concetti.
a) forza
La forza è il risultato quantitativo dell'impatto su un dato corpo da parte di altri corpi. La forza è una grandezza vettoriale (Fig. 1).
![]()
![]()
Punto A dell'inizio del vettore forza F chiamato punto di applicazione della forza. Viene chiamata la linea MN su cui si trova il vettore forza linea di forza. Viene chiamata la lunghezza del vettore forza, misurata su una certa scala valore numerico o modulo del vettore forza. Il modulo di forza è indicato come o . L'azione di una forza su un corpo si manifesta o nella sua deformazione, se il corpo è fermo, o nell'imprimergli accelerazione quando il corpo si muove. Su queste manifestazioni di forza si basa il dispositivo di vari strumenti (misuratori di forza o dinamometri) per misurare le forze.
b) sistema di forze
L'insieme considerato di forze si forma sistema di forza. Qualsiasi sistema costituito da n forze può essere scritto nella seguente forma: ![]()
c) corpo libero
Viene chiamato un corpo che può muoversi nello spazio in qualsiasi direzione senza sperimentare un'interazione diretta (meccanica) con altri corpi gratuito o isolato. L'influenza dell'uno o dell'altro sistema di forze su un corpo può essere chiarita solo se questo corpo è libero.
d) forza risultante
Se una forza ha lo stesso effetto su un corpo libero di un sistema di forze, allora viene chiamata questa forza risultante di questo sistema di forze. Questo è scritto come segue:
![]() ,
,
che significa equivalenza l'impatto sullo stesso corpo libero della risultante e di un qualche sistema di n forze.
Passiamo ora alla considerazione di concetti più complessi relativi alla determinazione quantitativa degli effetti rotazionali delle forze.
e) momento di forza rispetto a un punto (centro)
Se il corpo sotto l'azione di una forza può ruotare attorno a un punto fisso O (Fig. 2), allora per quantificare questo effetto rotatorio viene introdotta una quantità fisica, che si chiama momento di forza rispetto a un punto (centro).

Si chiama il piano passante per un dato punto fisso e la retta di azione della forza piano di forza. In Fig. 2, questo è il piano ОАВ.
Il momento di forza rispetto a un punto (centro) è una quantità vettoriale uguale al prodotto vettoriale del raggio vettore del punto di applicazione della forza per il vettore forza:
![]() ( 1)
( 1)
Secondo la regola della moltiplicazione vettoriale di due vettori, il loro prodotto vettoriale è un vettore perpendicolare al piano di posizione dei vettori dei fattori (in questo caso, il piano del triangolo OAB), diretto nella direzione da cui il giro più breve di il primo vettore fattore al secondo vettore fattore visibile contro l'orologio (Fig. 2). Con questo ordine dei vettori dei fattori del prodotto vettoriale (1), la rotazione del corpo sotto l'azione della forza sarà visibile contro l'orologio (Fig. 2) Poiché il vettore è perpendicolare al piano del forza, la sua posizione nello spazio determina la posizione del piano della forza.Il valore numerico del vettore del momento di forza rispetto al centro è uguale al doppio dell'area ОАВ e può essere determinato dalla formula:
![]() ,
(2)
,
(2)
dove grandezzah, uguale alla distanza più breve da un dato punto O alla retta di azione della forza, si chiama braccio della forza.
Se la posizione del piano di azione della forza nello spazio non è essenziale per caratterizzare l'azione rotazionale della forza, allora in questo caso, per caratterizzare l'azione rotazionale della forza, invece del vettore del momento della forza, momento algebrico di forza:
![]() (3)
(3)
Il momento di forza algebrico relativo a un dato centro è uguale al prodotto del modulo di forza e del suo spallamento, preso con un segno più o meno. In questo caso, un momento positivo corrisponde alla rotazione del corpo sotto l'azione di una data forza contro l'orologio, e un momento negativo corrisponde alla rotazione del corpo nella direzione dell'orologio. Dalle formule (1), (2) e (3) ne consegue il momento della forza rispetto a un punto è uguale a zero solo se il braccio di questa forzahzero. Una tale forza non può far ruotare il corpo attorno a un dato punto.
f) Momento della forza attorno all'asse
Se un corpo sotto l'azione di una forza può ruotare attorno a un asse fisso (ad esempio, la rotazione di un serramento nei cardini quando sono aperti o chiusi), allora viene introdotta una grandezza fisica per quantificare questo effetto rotatorio, che è chiamato momento di forza attorno ad un dato asse.
 z.z
z.z
b Fxy
La Figura 3 mostra un diagramma in base al quale viene determinato il momento di forza attorno all'asse z:
L'angolo è formato da due direzioni perpendicolari ze ai piani dei triangoli O ab e OAV, rispettivamente. Poiché O abè la proiezione di ОАВ sul piano xy, allora secondo il teorema della stereometria sulla proiezione di una figura piana su un dato piano, si ha:
dove il segno più corrisponde a un valore positivo di cos, cioè angoli acuti , e il segno meno corrisponde a un valore negativo di cos, cioè angoli ottusi , dovuti alla direzione del vettore . A sua volta SO ab=1/2ah, dove h ab . Il valore del segmento abè uguale alla proiezione della forza sul piano xy, cioè . ab = F xy .
Sulla base di quanto sopra, nonché delle uguaglianze (4) e (5), determiniamo il momento di forza attorno all'asse z come segue:
L'uguaglianza (6) ci consente di formulare la seguente definizione del momento di forza attorno a qualsiasi asse: il momento di forza attorno a un dato asse è uguale alla proiezione su questo asse del vettore del momento di questa forza rispetto a qualsiasi punto di un dato asse ed è definito come il prodotto della proiezione della forza su un piano perpendicolare all'asse dato, preso con un segno più o meno sulla spalla di questa proiezione rispetto al punto di intersezione dell'asse con il piano di proiezione. In questo caso, il segno del momento è considerato positivo se, guardando dalla direzione positiva dell'asse, è visibile la rotazione del corpo attorno a questo asse contro l'orologio. Altrimenti, il momento della forza attorno all'asse è considerato negativo. Poiché questa definizione del momento di forza rispetto all'asse è abbastanza difficile da ricordare, si consiglia di ricordare la formula (6) e la figura 3, che spiega questa formula.
Dalla formula (6) ne consegue il momento di forza intorno all'asse è nullo seè parallelo all'asse (in questo caso la sua proiezione su un piano perpendicolare all'asse è uguale a zero), oppure la linea di azione della forza interseca l'asse (quindi il braccio di proiezione h=0). Ciò corrisponde pienamente al significato fisico del momento di forza attorno all'asse come caratteristica quantitativa dell'azione rotazionale della forza su un corpo con un asse di rotazione.
g) peso corporeo
È stato a lungo notato che sotto l'influenza di una forza, il corpo aumenta gradualmente la velocità e continua a muoversi se la forza viene rimossa. Questa proprietà dei corpi, per resistere a un cambiamento nel loro movimento, è stata chiamata inerzia o inerzia dei corpi. La misura quantitativa dell'inerzia di un corpo è la sua massa. Oltretutto, la massa corporea è una misura quantitativa dell'effetto delle forze gravitazionali su un dato corpo maggiore è la massa del corpo, maggiore è la forza gravitazionale che agisce sul corpo. Come sarà mostrato di seguito, uh Queste due definizioni di peso corporeo sono correlate.
Altri concetti e definizioni di dinamica saranno discussi più avanti nelle sezioni in cui si verificano per la prima volta.
2. Legami e reazioni di legami
In precedenza nella sezione 1 punto (c) è stato dato il concetto di corpo libero, come un corpo che può muoversi nello spazio in qualsiasi direzione senza essere in contatto diretto con altri corpi. La maggior parte dei corpi reali che ci circondano sono in contatto diretto con altri corpi e non possono muoversi in una direzione o nell'altra. Quindi, ad esempio, i corpi situati sulla superficie del tavolo possono muoversi in qualsiasi direzione, ad eccezione della direzione perpendicolare alla superficie del tavolo verso il basso. Le porte a battente possono ruotare, ma non possono muoversi in avanti, ecc. Vengono chiamati corpi che non possono muoversi nello spazio in una direzione o nell'altra non gratis.
Tutto ciò che limita il movimento di un dato corpo nello spazio si chiama legame. Questi possono essere alcuni altri corpi che impediscono il movimento di questo corpo in alcune direzioni ( collegamenti fisici); più in generale, possono essere alcune condizioni imposte al movimento del corpo, che limitano questo movimento. Quindi, puoi impostare una condizione affinché il movimento di un punto materiale avvenga lungo una data curva. In questo caso, la connessione è specificata matematicamente sotto forma di un'equazione ( equazione di connessione). La questione dei tipi di collegamenti sarà considerata più dettagliatamente di seguito.
La maggior parte dei legami imposti ai corpi sono praticamente legami fisici. Pertanto, sorge la domanda sull'interazione di un dato corpo e sulla connessione imposta a questo corpo. A questa domanda risponde l'assioma sull'interazione dei corpi: due corpi agiscono l'uno sull'altro con forze uguali in grandezza, opposte in direzione e situate sulla stessa linea retta. Queste forze sono chiamate forze di interazione. Le forze di interazione vengono applicate a diversi corpi interagenti. Quindi, ad esempio, durante l'interazione di un dato corpo e una connessione, una delle forze di interazione viene applicata dal lato del corpo alla connessione e l'altra forza di interazione viene applicata dal lato della connessione al dato corpo . Quest'ultimo potere è chiamato forza di reazione del legame o semplicemente, reazione di connessione.
Quando si risolvono problemi pratici di dinamica, è necessario essere in grado di trovare la direzione delle reazioni di vari tipi di legami. La regola generale per determinare la direzione di una reazione di legame a volte può aiutare in questo: la reazione di un legame è sempre diretta nella direzione opposta alla direzione in cui questo legame impedisce il movimento di un dato corpo. Se questa direzione può essere specificata in modo definitivo, la reazione della connessione sarà determinata dalla direzione. Altrimenti, la direzione della reazione del legame è indefinita e può essere trovata solo dalle corrispondenti equazioni del moto o dell'equilibrio del corpo. Più in dettaglio, la questione dei tipi di legami e della direzione delle loro reazioni dovrebbe essere studiata secondo il libro di testo: S.M. Targ Un breve corso di meccanica teorica "Scuola superiore", M., 1986. Cap.1, §3.
Nella sezione 1, punto (c), è stato detto che l'effetto di qualsiasi sistema di forze può essere pienamente determinato solo se questo sistema di forze è applicato a un corpo libero. Poiché la maggior parte dei corpi, in effetti, non è libera, allora per studiare il movimento di questi corpi, sorge la domanda su come rendere liberi questi corpi. Questa domanda ha una risposta assioma delle connessioni delle lezioni Su filosofia in casa. Lezioni erano... psicologia sociale ed etnopsicologia. 3. Teorico risultati Nel darwinismo sociale erano ...
teorico Meccanica
Tutorial >> FisicaAstratto lezioni Su materia TEORICO MECCANICA Per gli studenti della specialità: 260501.65 ... - Abstract a tempo pieno lezioni compilato sulla base di: Butorin L.V., Busygina E.B. teorico Meccanica. Guida didattica e pratica...


